3.6: паралельні та перпендикулярні лінії

Last updated
Save as PDF

Page ID: 58113

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Визначте ухили паралельних і перпендикулярних ліній.
Знайти рівняння паралельних і перпендикулярних ліній

Визначення паралельних і перпендикулярних

Паралельні лінії - це лінії в одній площині, які ніколи не перетинаються. Дві невертикальні лінії в одній площині, з нахилами$m_{1}$ і$m_{2}$, паралельні, якщо їх нахили однакові,$m_{1}=m_{2}$. Розглянемо наступні два рядки:

Розглянемо відповідні їм графіки:

$Знімок екрана (628) .png$

Малюнок$\PageIndex{1}$

Обидві лінії мають нахил$m=\frac{3}{4}$ і, таким чином, паралельні.

Перпендикулярні лінії - це лінії в одній площині, які перетинаються під прямим кутом ($90$градусами). Дві невертикальні лінії в одній площині, з ухилами$m_{1}$ і$m_{2}$, перпендикулярні, якщо добуток їх нахилів є$−1: m1⋅m2=−1$. Ми можемо вирішити за$m_{1}$ і отримати$m_{1}=\frac{−1}{m_{2}}$. У такому вигляді ми бачимо, що перпендикулярні лінії мають нахили, які є негативними зворотними, або протилежними зворотними. Наприклад, якщо дано ухил

$m=-\frac{5}{8}$

то нахил перпендикулярної лінії протилежний взаємний:

$m_{\perp}=\frac{8}{5}$

Математичне позначення$m_{⊥}$ читається «$m$перпендикулярно». Ми можемо переконатися, що два укоси виробляють перпендикулярні лінії, якщо їх продукт є$−1$.

$m\cdot m_{\perp}=-\frac{5}{8}\cdot\frac{8}{5}=-\frac{40}{40}=-1\quad\color{Cerulean}{\checkmark}$

Геометрично зауважимо, що якщо лінія має позитивний нахил, то будь-яка перпендикулярна лінія матиме негативний нахил. Крім того, підйом і пробіг між двома перпендикулярними лініями змінюються місцями.

$Знімок екрана (629) .png$

Малюнок$\PageIndex{2}$

Перпендикулярні лінії мають нахили, протилежні взаємно, тому не забудьте знайти зворотний і змінити знак. Іншими словами,

Якщо$m=\frac{a}{b}$, то$m_{\perp}=-\frac{b}{a}$

Визначення нахилу перпендикулярної лінії можна виконати подумки. Нижче наведено кілька прикладів

Таблиця$\PageIndex{1}$
Заданий ухил	Ухил перпендикулярної лінії
$m=\frac{1}{2}$	$m_{\perp}=-2$
$m=-\frac{3}{4}$	$m_{\perp}=\frac{4}{3}$
$m=3$	$m_{\perp}=-\frac{1}{3}$
$m=-4$	$m_{\perp}=\frac{1}{4}$

Приклад$\PageIndex{1}$

Визначте нахил прямої паралельної$y=−5x+3$.

Рішення:

Оскільки дана лінія знаходиться в ухилі-перехоплення формі, ми можемо побачити, що її нахил є$m=−5$. При цьому нахил будь-якої лінії, паралельної даній лінії, повинен бути однаковим,$m_{∥}=−5$. Математичне позначення$m_{∥}$ говорить «$m$паралельно».

Відповідь:

$m_{∥}=−5$

Приклад$\PageIndex{2}$

Визначте нахил лінії перпендикулярно до$3x−7y=21$.

Рішення:

По-перше, вирішити для$y$ і висловити лінію у формі нахилу перехоплення.

У такому вигляді ми можемо бачити, що нахил даної лінії є$m=\frac{3}{7}$, і таким чином$m_{⊥}=−\frac{7}{3}$.

Відповідь:

$m_{⊥}=−\frac{7}{3}$

Вправа$\PageIndex{1}$

Знайдіть нахил лінії перпендикулярно$15x+5y=20$.

Відповідь: $m_{\perp}=\frac{1}{3}$

Пошук рівнянь паралельних і перпендикулярних ліній

Ми бачили, що графік прямої повністю визначається двома точками або однією точкою та її нахилом. Часто вас попросять знайти рівняння прямої з певним геометричним співвідношенням, наприклад, чи є лінія паралельною або перпендикулярною іншій лінії.

Приклад$\PageIndex{3}$

Знайти рівняння прямої, що проходить$(6, −1)$ і паралельно$y=\frac{1}{2}x+2$

Рішення

Тут дана лінія має нахил$m=\frac{1}{2}$, а нахил прямої паралельної дорівнює$m_{∥}=\frac{1}{2}$. Оскільки вам дано точку та нахил, використовуйте точку-нахил форми прямої для визначення рівняння.

$\begin{array}{cc}{\color{Cerulean}{Point}}&{\color{Cerulean}{Slope}}\\{(6,-1)}&{m_{\parallel}=\frac{1}{2}} \end{array}$

Відповідь:

$y=\frac{1}{2}x-4$

Важливо мати геометричне розуміння цього питання. Нас попросили знайти рівняння прямої, паралельної іншій лінії, що проходить через певну точку.

$Скріншот (630) .png$

Малюнок$\PageIndex{3}$

Через точку$(6, −1)$ ми знайшли паралельну лінію$y=\frac{1}{2}x−4$, показану пунктирною. Зверніть увагу, що нахил такий же, як і дана лінія, але$y$ -перехоплення відрізняється. Якщо мати на увазі геометричну інтерпретацію, то легше буде запам'ятати процес, необхідний для вирішення проблеми.

Приклад$\PageIndex{4}$

Знайти рівняння прямої, що проходить через$(−1, −5)$ і перпендикулярно до$y=−\frac{1}{4}x+2$.

Рішення:

Дана лінія має нахил$m=−\frac{1}{4}$, і таким чином$m_{⊥}=+\frac{4}{1}=4$. Заставте цей нахил і задану точку в точку-нахил форми.

$\begin{array}{cc} {\color{Cerulean}{Point}}&{\color{Cerulean}{Slope}}\\{(-1,-5)}&{m_{\perp}=4}\end{array}$

Відповідь:

$y=4x-1$

Геометрично ми бачимо, що лінія$y=4x−1$, показана пунктирним нижче, проходить наскрізь$(−1, −5)$ і перпендикулярна заданій лінії.

$Знімок екрана (631) .png$

Малюнок$\PageIndex{4}$

Не завжди так, що дана лінія знаходиться в ухилі-перехоплення формі. Часто доводиться виконувати додаткові кроки для визначення ухилу. Загальні кроки знаходження рівняння прямої викладені в наступному прикладі.

Приклад$\PageIndex{5}$

Знайти рівняння прямої, що проходить через$(8, −2)$ і перпендикулярно до$6x+3y=1$.

Рішення:

Крок 1: Знайдіть нахил$m$. Спочатку знайдіть нахил заданої лінії. Для цього вирішуйте$y$ для зміни стандартної форми на ухил-перехоплення форми,$y=mx+b$.

$\begin{aligned} 6x+3y&=1 \\ 6x+3y\color{Cerulean}{-6x}&=1\color{Cerulean}{-6x} \\ 3y&=-6x+1 \\ \frac{3y}{\color{Cerulean}{3}}&=\frac{-6x+1}{\color{Cerulean}{3}} \\ y&=\frac{-6x}{3}+\frac{1}{3}\\y&=-2x+\frac{1}{3} \end{aligned}$

У такому вигляді можна побачити, що нахил є$m=−2=−\frac{2}{1}$, і таким чином$m_{⊥}=\frac{−1}{−2}=+\frac{1}{2}$.

Крок 2: Замініть знайдений нахил та задану точку у форму рівняння точки-нахилу для прямої. При цьому нахил є$m_{⊥}=\frac{1}{2}$ і задана точка є$(8, −2)$.

$\begin{aligned} y-y_{1}&=m(x-x_{1}) \\ y-(-2)&=\frac{1}{2}(x-8) \end{aligned}$

Крок 3: Вирішіть для$y$.

Відповідь:

$y=\frac{1}{2}x−6$

Приклад$\PageIndex{6}$

Знайти рівняння прямої, що проходить через$(\frac{7}{2}, 1)$ і паралельно$2x+14y=7$.

Рішення:

Знайдіть нахил,$m$ вирішивши для$y$.

$\begin{aligned} 2x+14y&=7 \\ 2x+14y\color{Cerulean}{-2x}&=7\color{Cerulean}{-2x} \\ 14y&=-2x+7 \\ \frac{14y}{\color{Cerulean}{14}}&=\frac{-2x+7}{\color{Cerulean}{14}} \\ y&=\frac{-2x}{14}+\frac{7}{14} \\ y&=-\frac{1}{7}x+\frac{1}{2} \end{aligned}$

Дана лінія має нахил$m=−\frac{1}{7}$, і т$m_{∥}=−\frac{1}{7}$. Використовуємо це і точку$(\frac{7}{2}, 1)$ в точково-нахиленій формі.

$\begin{aligned} y-y_{1}&=m(x-x_{1}) \\ y-1&=-\frac{1}{7}\left(x-\frac{7}{2} \right) \\ y-1&=-\frac{1}{7}x+\frac{1}{2} \\ y-1\color{Cerulean}{+1}&=-\frac{1}{7}x+\frac{1}{2}\color{Cerulean}{+1} \\ y&=-\frac{1}{7}x+\frac{1}{2}+\color{Cerulean}{\frac{2}{2}} \\ y&=-\frac{1}{7}x+\frac{3}{2} \end{aligned}$

Відповідь:

$y=-\frac{1}{7}x+\frac{3}{2}$

Вправа$\PageIndex{2}$

Знайдіть рівняння прямої перпендикулярної$x−3y=9$ і проходить через неї$(−\frac{1}{2}, 2)$.

Відповідь: $y=-3x+\frac{1}{2}$

При знаходженні рівняння прямої, перпендикулярної горизонтальній або вертикальній лінії, найкраще розглянути геометричну інтерпретацію.

Приклад$\PageIndex{7}$

Знайти рівняння прямої, що проходить через$(−3, −2)$ і перпендикулярно до$y=4$.

Рішення:

Ми визнаємо, що$y=4$ це горизонтальна лінія, і ми хочемо знайти перпендикулярну лінію, що проходить через$(−3, −2)$.

$Знімок екрана (632) .png$

Малюнок$\PageIndex{5}$

Якщо провести лінію перпендикулярно заданій горизонтальній лінії, то в результаті вийде вертикальна лінія.

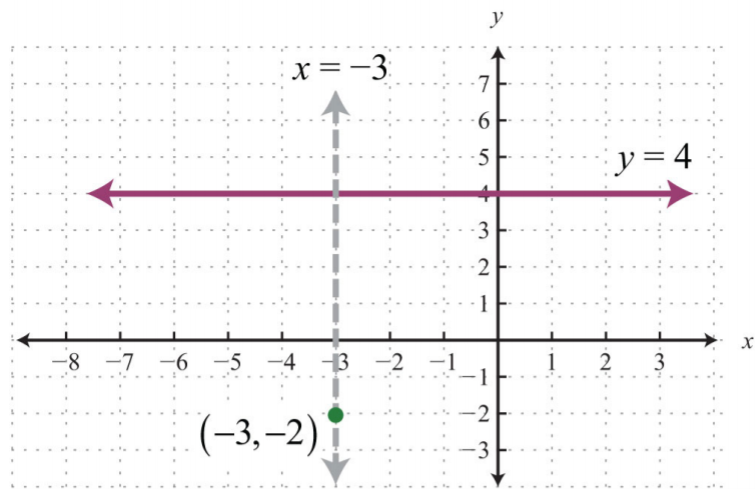$Знімок екрана (633) .png$

Малюнок$\PageIndex{6}$

Рівняння вертикальних ліній виглядають так$x=k$. Оскільки він повинен пройти$(−3, −2)$, робимо висновок, що$x=−3$ це рівняння. Усі впорядковані парні рішення вертикальної лінії повинні мати однакову$x$ -координату.

Відповідь:

$x=−3$

Ми можемо переписати рівняння будь-якої горизонтальної лінії$y=k$, у вигляді нахилу-перехоплення наступним чином:

$y=0x+k$

Написано в такому вигляді, ми бачимо, що нахил є$m=0=\frac{0}{1}$. Якщо ми спробуємо знайти нахил перпендикулярної лінії, знайшовши протилежну взаємну, ми зіткнемося з проблемою:$m_{⊥}=−\frac{1}{0}$, яка не визначена. Ось чому ми подбали про обмеження визначення двома невертикальними лініями. Пам'ятайте, що горизонтальні лінії розташовуються перпендикулярно вертикальним лініям.

Ключові винос

Паралельні лінії мають однаковий нахил.
Перпендикулярні лінії мають нахили, протилежні взаємно. Іншими словами, якщо$m=\frac{a}{b}$, то$m_{⊥}=−\frac{b}{a}$.
Щоб знайти рівняння прямої, спочатку використовуйте задану інформацію для визначення нахилу. Потім використовуйте нахил і точку на лінії, щоб знайти рівняння, використовуючи форму точка-нахил.
Горизонтальні і вертикальні лінії розташовуються перпендикулярно один одному.

Вправа$\PageIndex{3}$ Parallel and Perpendicular Lines

Визначте нахил паралельних ліній і перпендикулярних ліній.

$y=−\frac{3}{4}x+8$
$y=\frac{1}{2}x−3$
$y=4x+4$
$y=−3x+7$
$y=−\frac{5}{8}x−12$
$y=\frac{7}{3}x+\frac{3}{2}$
$y=9x−25$
$y=−10x+15$
$y=5$
$x=−12$
$x−y=0$
$x+y=0$
$4x+3y=0$
$3x−5y=10$
$−2x+7y=14$
$−x−y=\frac{1}{5}$
$\frac{1}{2}x−\frac{1}{3}y=−1$
$−\frac{2}{3}x+\frac{4}{5}y=8$
$2x−\frac{1}{5}y=\frac{1}{10}$
$−\frac{4}{5}x−2y=7$

Відповідь

1. $m_{∥}=−\frac{3}{4}$і$m_{⊥}=\frac{4}{3}$

3. $m_{∥}=4$і$m_{⊥}=−\frac{1}{4}$

5. $m_{∥}=−\frac{5}{8}$і$m_{⊥}=\frac{8}{5}$

7. $m_{∥}=9$і$m_{⊥}=−\frac{1}{9}$

9. $m_{∥}=0$і$m_{⊥}$ невизначено

11. $m_{∥}=1$і$m_{⊥}=−1$

13. $m_{∥}=−\frac{4}{3}$і$m_{⊥}=\frac{3}{4}$

15. $m_{∥}=\frac{2}{7}$і$m_{⊥}=−\frac{7}{2}$

17. $m_{∥}=\frac{3}{2}$і$m_{⊥}=−\frac{2}{3}$

19. $m_{∥}=10$і$m_{⊥}=−\frac{1}{10}$

Вправа$\PageIndex{4}$ Parallel and Perpendicular Lines

Визначте, чи є лінії паралельними, перпендикулярними чи ні.

$\left\{\begin{aligned}y&=\frac{2}{3}x+3\\y&=\frac{2}{3}x−3\end{aligned}\right.$
$\left\{\begin{aligned}y&=\frac{3}{4}x−1\\y&=\frac{4}{3}x+3\end{aligned}\right.$
$\left\{\begin{aligned}y&=−2x+1\\ y&=\frac{1}{2}x+8\end{aligned}\right.$
$\left\{\begin{aligned}y&=3x−\frac{1}{2}\\ y&=3x+2\end{aligned}\right.$
$\left\{\begin{aligned}y&=5\\x&=−2\end{aligned}\right.$
$\left\{\begin{aligned}y&=7\\y&=−\frac{1}{7}\end{aligned}\right.$
$\left\{\begin{aligned}3x−5y&=15\\ 5x+3y&=9\end{aligned}\right.$
$\left\{\begin{aligned}x−y&=7\\3x+3y&=2\end{aligned}\right.$
$\left\{\begin{aligned}2x−6y&=4\\−x+3y&=−2 \end{aligned}\right.$
$\left\{\begin{aligned}−4x+2y&=3\\6x−3y&=−3 \end{aligned}\right.$
$\left\{\begin{aligned}x+3y&=9\\2x+3y&=6 \end{aligned}\right.$
$\left\{\begin{aligned}y−10&=0\\x−10&=0 \end{aligned}\right.$
$\left\{\begin{aligned}y+2&=0\\2y−10&=0 \end{aligned}\right.$
$\left\{\begin{aligned}3x+2y&=6\\2x+3y&=6 \end{aligned}\right.$
$\left\{\begin{aligned}−5x+4y&=20\\10x−8y&=16 \end{aligned}\right.$
$\left\{\begin{aligned}\frac{1}{2}x−\frac{1}{3}y&=1\\\frac{1}{6}x+\frac{1}{4}y&=−2\end{aligned}\right.$

Відповідь

1. Паралельний

3. Перпендикуляр

5. Перпендикуляр

7. Перпендикуляр

9. Паралельний

11. Ні

13. Паралельний

15. Паралельний

Вправа$\PageIndex{5}$ Equations in Point-Slope Form

Знайти рівняння прямої

Паралельно$y=\frac{1}{2}x+2$ і проходячи наскрізь$(6, −1)$.
Паралельно$y=−\frac{3}{4}x−3$ і проходячи наскрізь$(−8, 2)$.
Перпендикулярно$y=3x−1$ і проходить наскрізь$(−3, 2)$.
Перпендикулярно$y=−\frac{1}{3}x+2$ і проходить наскрізь$(4, −3)$.
Перпендикулярно$y=−2$ і проходить наскрізь$(−1, 5)$.
Перпендикулярно$x=\frac{1}{5}$ і проходить наскрізь$(5, −3)$.
Паралельно$y=3$ і проходячи наскрізь$(2, 4)$.
Паралельно$x=2$ і проходить через (7, −3)\).
Перпендикулярно$y=x$ і проходить наскрізь$(7, −13)$.
Перпендикулярно$y=2x+9$ і проходить наскрізь$(3, −1)$.
Паралельно$y=\frac{1}{4}x−5$ і проходячи наскрізь$(−2, 1)$.
Паралельно$y=−\frac{3}{4}x+1$ і проходячи наскрізь$(4, \frac{1}{4})$.
Паралельно$2x−3y=6$ і проходячи наскрізь$(6, −2)$.
Паралельно$−x+y=4$ і проходячи наскрізь$(9, 7)$.
Перпендикулярно$5x−3y=18$ і проходить наскрізь$(−9, 10)$.
Перпендикулярно$x−y=11$ і проходить наскрізь$(6, −8)$.
Паралельно$\frac{1}{5}x−\frac{1}{3}y=2$ і проходячи наскрізь$(−15, 6)$.
Паралельно$−10x−\frac{5}{7}y=12$ і проходячи наскрізь$(−1, \frac{1}{2})$.
Перпендикулярно$\frac{1}{2}x−\frac{1}{3}y=1$ і проходить наскрізь$(−10, 3)$.
Перпендикулярно$−5x+y=−1$ і проходить наскрізь$(−4, 0)$.
Паралельно$x+4y=8$ і проходячи наскрізь$(−1, −2)$.
Паралельно$7x−5y=35$ і проходячи наскрізь$(2, −3)$.
Перпендикулярно$6x+3y=1$ і проходить наскрізь$(8, −2)$.
Перпендикулярно$−4x−5y=1$ і проходить наскрізь$(−1, −1)$.
Паралельно$−5x−2y=4$ і проходячи наскрізь$(\frac{1}{5}, −\frac{1}{4})$.
Паралельно$6x−\frac{3}{2}y=9$ і проходячи наскрізь$(\frac{1}{3}, \frac{2}{3})$.
Перпендикулярно$y−3=0$ і проходить наскрізь$(−6, 12)$.
Перпендикулярно$x+7=0$ і проходить наскрізь$(5, −10)$.

Відповідь

1. $y=\frac{1}{2}x−4$

3. $y=−\frac{1}{3}x+1$

5. $x=−1$

7. $y=4$

9. $y=−x−6$

11. $y=\frac{1}{4}x+\frac{3}{2}$

13. $y=\frac{2}{3}x−6$

15. $y=−\frac{3}{5}x+\frac{23}{5}$

17. $y=\frac{3}{5}x+15$

19. $y=−\frac{2}{3}x−\frac{11}{3}$

21. $y=−\frac{1}{4}x−\frac{9}{4}$

23. $y=\frac{1}{2}x−6$

25. $y=−\frac{5}{2}x+\frac{1}{4}$

27. $x=−6$

Заданий ухил	Ухил перпендикулярної лінії
\(m=\frac{1}{2}\)	\(m_{\perp}=-2\)
\(m=-\frac{3}{4}\)	\(m_{\perp}=\frac{4}{3}\)
\(m=3\)	\(m_{\perp}=-\frac{1}{3}\)
\(m=-4\)	\(m_{\perp}=\frac{1}{4}\)