9.4: Біноміальна теорема

Last updated
Save as PDF

Page ID: 58170

Anonymous
LibreTexts

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Оцініть вирази за участю факторіалів.
Обчисліть біноміальні коефіцієнти.
Розширити повноваження біноміалів за допомогою біноміальної теореми.

Факторіали та біноміальний коефіцієнт

Почнемо з визначення факторіала ²⁵ натурального числа\(n\), позначеного\(n!\), як добуток всіх натуральних чисел менше або дорівнює\(n\).

\(n !=n(n-1)(n-2) \cdots 3 \cdot 2 \cdot 1\)

Наприклад,

\(\begin{array}{l}{7 !=7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=5,040 \quad\color{Cerulean}{Seven\:factorial}} \\[4pt] {5 !=5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=120\quad\quad\quad\quad\:\color{Cerulean}{Five\:factorial}} \\[4pt] {3 !=3 \cdot 2 \cdot 1=6\quad\quad\quad\quad\quad\quad\:\:\:\quad\color{Cerulean}{Three\:factorial}} \\[4pt] {1 !=1=1\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\color{Cerulean}{One\:factorial}}\end{array}\)

Визначимо нульовий факторіал ²⁶ рівним\(1\),

\(0 !=1 \quad\color{Cerulean}{Zero\:factorial}\)

Факторіал від'ємного числа не визначено.

На більшості сучасних калькуляторів ви знайдете факторіальну функцію. Деякі калькулятори не передбачають кнопку, присвячену йому. Однак його зазвичай можна знайти в системі меню, якщо таке передбачено.

Факторіал також може бути виражений за допомогою наступного відношення повторення,

\(n !=n(n-1) !\)

Наприклад, факторіал\(8\) може бути виражений у вигляді добутку\(8\) і\(7!\):

\(\begin{aligned} 8 ! &=8 \cdot \color{Cerulean}{7 !} \\[4pt] &=8 \cdot \color{Cerulean}{7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \\[4pt] &=40,320 \end{aligned}\)

При роботі з співвідношеннями за участю факторіалів часто трапляється, що багато факторів скасовують.

Приклад\(\PageIndex{1}\)

Оцініть:\(\frac{12 !}{6 !}\).

Рішення

\(\begin{aligned} \frac{12 !}{6 !}&=\frac{12 \cdot 11 \cdot 10 \cdot 9 \cdot 8 \cdot 7 \cdot \color{Cerulean}{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}}{\color{Cerulean}{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}}\\[4pt] &=\frac{12\cdot11\cdot10\cdot9\cdot8\cdot7 \cdot \cancel{6!}}{\cancel{6!}} \\[4pt] &=12\cdot11\cdot10\cdot9\cdot8\cdot7\\[4pt] &=665,280\end{aligned}\)

Відповідь

\(665,280\)

Біноміальний коефіцієнт ²⁷, що позначається\(_{n} C_{k}=\left( \begin{array}{l}{n} \\[4pt] {k}\end{array}\right)\), читається «\(n\)вибрати\(k\)» і задається за такою формулою:

\(_{n} C_{k}=\left( \begin{array}{l}{n} \\[4pt] {k}\end{array}\right)=\frac{n !}{k !(n-k) !}\)

Ця формула дуже важлива в галузі математики під назвою комбінаторика. Це дає кількість способів\(k\) вибору елементів з набору\(n\) елементів, де порядок не має значення. У цьому розділі нас турбує можливість обчислити цю величину.

Приклад\(\PageIndex{2}\)

Розрахувати\(\left( \begin{array}{l}{7} \\[4pt] {3}\end{array}\right)\).

Рішення

Використовуйте формулу для біноміального коефіцієнта,

\(\left( \begin{array}{l}{n} \\[4pt] {k}\end{array}\right)=\frac{n !}{k !(n-k) !}\)

де\(n = 7\) і\(k = 3\). Після заміни шукайте фактори для скасування.

\(\begin{aligned} \left( \begin{array}{l}{7} \\[4pt] {3}\end{array}\right) &=\frac{7 !}{3 !(7-3) !} \\[4pt] &=\frac{7 !}{3 ! 4 !} \\[4pt] &=\frac{7\cdot6\cdot5\cdot\cancel{\color{Cerulean}{4!}}}{3! \cancel{\color{Cerulean}{4!}}} \\[4pt]&=\frac{210}{6} \\[4pt] &=35\end{aligned}\)

Відповідь:

\(35\)

Перевірте систему меню вашого калькулятора для функції, яка обчислює цю величину. Шукайте позначення\(_{n} C_{k}\) в підрозділі ймовірності.

Вправа\(\PageIndex{1}\)

Розрахувати\(\left( \begin{array}{l}{8} \\[4pt] {5}\end{array}\right)\).

Відповідь

\(56\)

www.youtube.com/В/РПБ8КД1ХГК

Розглянемо наступний двочлен, піднятий до\(3^{rd}\) влади в розширеному вигляді:

\((x+y)^{3}=x^{3}+3 x^{2} y+3 x y^{2}+y^{3}\)

Порівняйте його з наступними розрахунками,

\(\left( \begin{array}{l}{3} \\[4pt] {0}\end{array}\right)=\dfrac{3 !}{0 !(3-0) !}=\frac{3 !}{1 \cdot 3 !}=1\)
\(\left( \begin{array}{l}{3} \\[4pt] {1}\end{array}\right)=d\frac{3 !}{1 !(3-1) !}=\frac{3 \cdot 2 !}{1 \cdot 2 !}=3\)
\(\left( \begin{array}{l}{3} \\[4pt] {2}\end{array}\right)=\dfrac{3 !}{2 !(3-2) !}=\frac{3 \cdot 2 !}{2 !}=3\)
\(\left( \begin{array}{c}{3} \\[4pt] {3}\end{array}\right)=\dfrac{3 !}{3 !(3-3) !}=\frac{3 !}{3 ! 0 !}=1\)

Зверніть увагу, що між цими розрахунками і коефіцієнтами розширеного біноміала існує зв'язок. Це спостереження узагальнено в наступному розділі.

Біноміальна теорема

Розглянемо розширення\((x+2)^{5} \):

\((x+2)^{5}=(x+2)(x+2)(x+2)(x+2)(x+2)\)

Один швидко розуміє, що це дуже виснажливий розрахунок, що включає кілька застосувань розподільної власності. Біноміальна теорема ²⁸ забезпечує метод розширення біномів, піднятих до степенів без прямого множення кожного коефіцієнта:

\((x+y)^{n}=\left( \begin{array}{c}{n} \\[4pt] {0}\end{array}\right) x^{n} y^{0}+\left( \begin{array}{c}{n} \\[4pt] {1}\end{array}\right) x^{n-1} y^{1}+\left( \begin{array}{c}{n} \\[4pt] {2}\end{array}\right) x^{n-2} y^{2}+\ldots+\left( \begin{array}{c}{n} \\[4pt] {n-1}\end{array}\right) x^{1} y^{n-1}\)

Більш компактно ми можемо написати,

\[(x+y)^{n}=\sum_{k=0}^{n} \left( \begin{array}{l}{n} \\[4pt] {k}\end{array}\right) x^{n-k} y^{k} \quad \color{Cerulean}{Binomial\:theorem} \nonumber\]

Приклад\(\PageIndex{3}\)

Розгорніть за допомогою біноміальної теореми:\((x + 2)^{5}\).

Рішення

Використовуйте біноміальну теорему де\(n = 5\) і\(y = 2\).

\((x+2)^{5}=\left( \begin{array}{l}{5} \\[4pt] {0}\end{array}\right) x^{5} 2^{0}+\left( \begin{array}{c}{5} \\[4pt] {1}\end{array}\right) x^{4} 2^{1}+\left( \begin{array}{l}{5} \\[4pt] {2}\end{array}\right) x^{3} 2^{2}+\left( \begin{array}{l}{5} \\[4pt] {3}\end{array}\right) x^{2} 2^{3}+\left( \begin{array}{l}{5} \\[4pt] {4}\end{array}\right) x^{1}2^{4}\)

Іноді корисно визначити закономірність, яка виникає в результаті застосування біноміальної теореми. Зверніть увагу, що повноваження змінної\(x\) починаються\(5\) і зменшуються до нуля. Повноваження постійного терміну починаються з\(0\) і збільшуються до\(5\). Біноміальні коефіцієнти можна обчислити в сторону і залишати читачеві як вправу.

\(\begin{aligned}(x+2)^{5} &=\left( \begin{array}{c}{5} \\[4pt] {0}\end{array}\right) x^{5} 2^{0}+\left( \begin{array}{c}{5} \\[4pt] {1}\end{array}\right) x^{4} 2^{1}+\left( \begin{array}{c}{5} \\[4pt] {2}\end{array}\right) x^{3} 2^{2}+\left( \begin{array}{c}{5} \\[4pt] {3}\end{array}\right) x^{2} 2^{3}+\left( \begin{array}{c}{5} \\[4pt] {4}\end{array}\right) x^{1} 2^{4} \\[4pt] &=1 x^{5} \times 1+5 x^{4} \times 2+10 x^{3} \times 4+10 x^{2} \times 8+5 x^{1} \times 16+1 \times 1 \\[4pt] &=x^{5}+10 x^{4}+40 x^{3}+80 x^{2}+80 x+32 \end{aligned}\)

Відповідь

\(x^{5}+10 x^{4}+40 x^{3}+80 x^{2}+80 x+32\)

Біноміал може мати негативні члени, і в цьому випадку ми отримаємо чергуваний ряд.

Приклад\(\PageIndex{4}\)

Розгорніть за допомогою біноміальної теореми:\((u − 2v)^{4}\).

Рішення

Використовуйте біноміальну теорему де\(n = 4, x = u\),\(y = −2v\) а потім спрощуйте кожен член.

\(\begin{aligned}(u-2 v)^{4} &=\left( \begin{array}{c}{4} \\[4pt] {0}\end{array}\right) u^{4}(-2 v)^{0}+\left( \begin{array}{c}{4} \\[4pt] {1}\end{array}\right) u^{3}(-2 v)^{1}+\left( \begin{array}{c}{4} \\[4pt] {2}\end{array}\right) u^{2}(-2 v)^{2}+\left( \begin{array}{c}{4} \\[4pt] {3}\end{array}\right) u^{1}(-2v)^{3} + \left(\begin{array}{c}4 \\[4pt]4 \end{array} \right)u^{0}(-2v)^{4} \\[4pt] &=1 \times u^{4} \times 1+4 u^{3}(-2 v)+6 u^{2}\left(4 v^{2}\right)+4 u\left(-8 v^{3}\right) + 16v^{4} \\[4pt] &=u^{4}-8 u^{3} v+24 u^{2} v^{2}-32 u v^{3}+16 v^{4} \end{aligned}\)

Відповідь

\(u^{4}-8 u^{3} v+24 u^{2} v^{2}-32 u v^{3}+16 v^{4}\)

Вправа\(\PageIndex{2}\)

Розгорніть за допомогою біноміальної теореми:\(\left(a^{2}-3\right)^{4}\)

Відповідь

\(a^{8}-12 a^{6}+54 a^{4}-108 a^{2}+81\)

www.youtube.com/В/WICBQMOA4T4

Далі вивчаємо коефіцієнти розширень\((x + y)^{n}\) починаючи з\(n = 0\):

\[ \begin{align*} (x+y)^{0} &=1 \\[4pt] (x+y)^{1}&=x+y \\[4pt] (x+y)^{2}&=x+y \\[4pt] (x+y)^{3}&=x^{2}+2 x y+y^{2} \\[4pt] (x+y)^{3}&=x^{3}+3 x^{2} y+3 x y^{2}+y^{3} \\[4pt] (x+y)^{4}&=x^{4}+4 x^{3} y+6 x^{2} y^{2}+4 x y^{3}+y^{4} \end{align*}\]

Запишіть коефіцієнти в трикутний масив і зверніть увагу, що кожне число нижче є сумою двох чисел над ним, завжди залишаючи a\(1\) на будь-якому кінці.

Це трикутник Паскаля ²⁹; він забезпечує швидкий метод обчислення біноміальних коефіцієнтів. Використовуйте це спільно з біноміальною теоремою для впорядкування процесу розширення біномів, піднятих до повноважень. Наприклад, для розширення\((x − 1)^{6}\) нам знадобиться ще два ряди трикутника Паскаля,

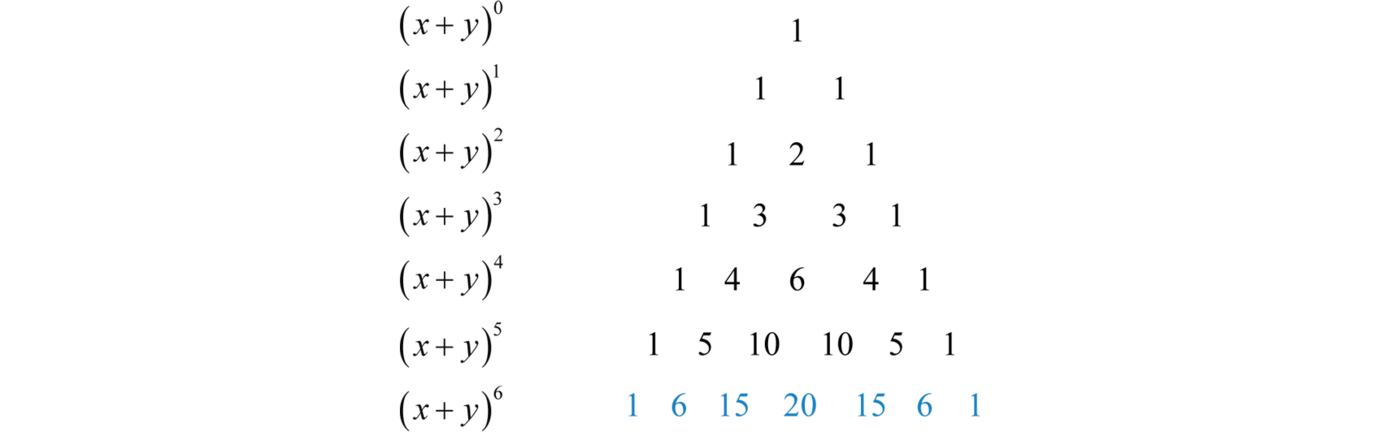
Біноміальні коефіцієнти, які нам потрібні, синього кольору. Використовуйте ці числа та біноміальну теорему, щоб швидко розширити\((x − 1)^{6}\) наступним чином:

\(\begin{aligned}(x-1)^{6} &=1 x^{6}(-1)^{0}+6 x^{5}(-1)^{1}+15 x^{4}(-1)^{2}+20 x^{3}(-1)^{3}+15 x^{2}(-1)^{4}+6 x(-1)^{5} \\[4pt] &=x^{6}-6 x^{5}+15 x^{4}-20 x^{3}+15 x^{2}-6 x+1 \end{aligned}\)

Приклад\(\PageIndex{5}\)

Розгорніть за допомогою біноміальної теореми та трикутника Паскаля:\((2x − 5)^{4}\).

Рішення

З трикутника Паскаля ми бачимо, що коли\(n = 4\) біноміальні коефіцієнти є\(1, 4, 6, 4\),\(1\) і.Використовуйте ці числа та біноміальну теорему наступним чином:

\(\begin{aligned}(2 x-5)^{4} &=1(2 x)^{4}(-5)^{0}+4(2 x)^{3}(-5)^{1}+6(2 x)^{2}(-5)^{2}+4(2 x)^{1}(-5)^{3}+(2 x)^{0}(-5)^{4} \\[4pt] &=16 x^{4} \cdot 1+4 \cdot 8 x^{3}(-5)+6 \cdot 4 x^{2} \cdot 25+4 \cdot 2 x(-125)+1 \cdot 625 \\[4pt] &=16 x^{4}-160 x^{3}+600 x^{2}-1,000 x+625 \end{aligned}\)

Відповідь:

\(16 x^{4}-160 x^{3}+600 x^{2}-1,000 x+625\)

Ключові винос

Щоб обчислити факторіал натурального числа, помножте це число на всі натуральні числа, менші за нього:\(5! = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 120\). Пам'ятайте, що ми визначили\(0! = 1\).
Біноміальні коефіцієнти - це цілі числа, обчислені за формулою:\[\left( \begin{array}{l}{n} \\[4pt] {k}\end{array}\right)=\frac{n !}{k !(n-k) !}. \nonumber\]
Біноміальна теорема забезпечує метод розширення біноміалів, піднятих до степенів без прямого множення кожного коефіцієнта:\[(x+y)^{n}=\sum_{k=0}^{n} \left( \begin{array}{l}{n} \\[4pt] {k}\end{array}\right) x^{n-k} y^{k}\nonumber\]
Використовуйте трикутник Паскаля, щоб швидко визначити біноміальні коефіцієнти.

Вправа\(\PageIndex{3}\)

Оцінити.

\(6!\)
\(4!\)
\(10!\)
\(9!\)
\(\frac{6 !}{3 !}\)
\(\frac{8 !}{4 !}\)
\(\frac{13 !}{9 !}\)
\(\frac{15 !}{10 !}\)
\(\frac{12 !}{3 ! 7 !}\)
\(\frac{10 !}{2 ! 5 !}\)
\(\frac{n !}{(n-2) !}\)
\(\frac{(n+1) !}{(n-1) !}\)
(а)\(4 !+3 !\) (б)\((4+3) !\)
(а)\(4 !-3 !\) (б)\((4-3) !\)

Відповідь

1. \(720\)

3. \(3,628,800\)

5. \(120\)

7. \(17,160\)

9. \(15,840\)

11. \(n^{2} − n\)

13. а.\(30\) б.\(5,040\)

Вправа\(\PageIndex{4}\)

Перепишіть за допомогою факторіальних позначень.

\(1 \times 2 \times 3 \times 4 \times 5 \times 6 \times 7\)
\(1 \times 2 \times 3 \times 4 \times 5\)
\(15 \times 14 \times 13\)
\(10 \times 9 \times 8 \times 7\)
\(13\)
\(8 \times 7\)
\(n(n-1)(n-2)\)
\(1 \times 2 \times 3 \times \cdots \times n \times(n+1)\)

Відповідь

1. \(7!\)

3. \(\frac{15 !}{12 !}\)

5. \(\frac{13 !}{12 !}\)

7. \(\frac{n !}{(n-3) !}\)

Вправа\(\PageIndex{5}\)

Обчисліть вказаний біноміальний коефіцієнт.

\(\left( \begin{array}{l}{6} \\[4pt] {4}\end{array}\right)\)
\(\left( \begin{array}{l}{8} \\[4pt] {4}\end{array}\right)\)
\(\left( \begin{array}{l}{7} \\[4pt] {2}\end{array}\right)\)
\(\left( \begin{array}{l}{9} \\[4pt] {5}\end{array}\right)\)
\(\left( \begin{array}{l}{9} \\[4pt] {0}\end{array}\right)\)
\(\left( \begin{array}{l}{13} \\[4pt] {12}\end{array}\right)\)
\(\left( \begin{array}{l}{n} \\[4pt] {0}\end{array}\right)\)
\(\left( \begin{array}{l}{n} \\[4pt] {n}\end{array}\right)\)
\(\left( \begin{array}{l}{n} \\[4pt] {1}\end{array}\right)\)
\(\left( \begin{array}{c}{n} \\[4pt] {n-1}\end{array}\right)\)
\(_{10} C_{8}\)
\(_{5} C_{1}\)
\(_{12} C_{12}\)
\(_{10} C_{5}\)
\(_{n} C_{n-2}\)
\(_{n} C_{n-3}\)

Відповідь

1. \(15\)

3. \(21\)

5. \(1\)

7. \(1\)

9. \(n\)

11. \(45\)

13. \(1\)

15. \(\frac{n^{2}-n}{2}\)

Вправа\(\PageIndex{6}\)

Розгорніть за допомогою біноміальної теореми.

\((4 x-3)^{3}\)
\((2 x-5)^{3}\)
\(\left(\frac{x}{2}+y\right)^{3}\)
\(\left(x+\frac{1}{y}\right)^{3}\)
\((x+3)^{4}\)
\((x+5)^{4}\)
\((x-4)^{4}\)
\((x-2)^{4}\)
\(\left(x+\frac{2}{y}\right)^{4}\)
\(\left(\frac{x}{3}-y\right)^{4}\)
\((x+1)^{5}\)
\((x-3)^{5}\)
\((x-2)^{6}\)
\((x+1)^{6}\)
\((x-1)^{7}\)
\((x+1)^{7}\)
\((5 x-1)^{4}\)
\((3 x-2)^{4}\)
\((4 u+v)^{4}\)
\((3 u-v)^{4}\)
\((u-5 v)^{5}\)
\((2 u+3 v)^{5}\)
\(\left(a-b^{2}\right)^{5}\)
\(\left(a^{2}+b^{2}\right)^{4}\)
\(\left(a^{2}+b^{4}\right)^{6}\)
\(\left(a^{5}+b^{2}\right)^{5}\)
\((x+\sqrt{2})^{3}\)
\((x-\sqrt{2})^{4}\)
\((\sqrt{x}-\sqrt{y})^{4}, x, y \geq 0\)
\((\sqrt{x}+2 \sqrt{y})^{5}, x, y \geq 0\)
\((x+y)^{7}\)
\((x+y)^{8}\)
\((x+y)^{9}\)
\((x-y)^{7}\)
\((x-y)^{8}\)
\((x-y)^{9}\)

Відповідь

1. \(64 x^{3}-144 x^{2}+108 x-27\)

3. \(\frac{x^{3}}{8}+\frac{3 x^{2} y}{4}+\frac{3 x y^{2}}{2}+y^{3}\)

5. \(x^{4}+12 x^{3}+54 x^{2}+108 x+81\)

7. \(x^{4}-16 x^{3}+96 x^{2}-256 x+256\)

9. \(x^{4}+\frac{8 x^{3}}{y}+\frac{24 x^{2}}{y^{2}}+\frac{32 x}{y^{3}}+\frac{16}{y^{4}}\)

11. \(x^{5}+5 x^{4}+10 x^{3}+10 x^{2}+5 x+1\)

13. \(x^{6}-12 x^{5}+60 x^{4}-160 x^{3}+240 x^{2}-192 x+64\)

15. \(x^{7}-7 x^{6}+21 x^{5}-35 x^{4}+35 x^{3}-21 x^{2}+7 x-1\)

17. \(625 x^{4}-500 x^{3}+150 x^{2}-20 x+1\)

19. \(256 u^{4}+256 u^{3} v+96 u^{2} v^{2}+16 u v^{3}+v^{4}\)

21. \(\begin{array}{l}{u^{5}-25 u^{4} v+250 u^{3} v^{2}-1,250 u^{2} v^{3}} {+3,125 u v^{4}-3,125 v^{5}}\end{array}\)

23. \(a^{5}-5 a^{4} b^{2}+10 a^{3} b^{4}-10 a^{2} b^{6}+5 a b^{8}-b^{10}\)

25. \(\begin{array}{l}{a^{12}+6 a^{10} b^{4}+15 a^{8} b^{8}+20 a^{6} b^{12}} {+15 a^{4} b^{16}+6 a^{2} b^{20}+b^{24}}\end{array}\)

27. \(x^{3}+3 \sqrt{2} x^{2}+6 x+2 \sqrt{2}\)

29. \(x^{2}-4 x \sqrt{x y}+6 x y-4 y \sqrt{x y}+y^{2}\)

31. \(\begin{array}{l}{x^{7}+7 x^{6} y+21 x^{5} y^{2}+35 x^{4} y^{3}} {+35 x^{3} y^{4}+21 x^{2} y^{5}+7 x y^{6}+y^{7}}\end{array}\)

33. \(\begin{array}{l}{x^{9}+9 x^{8} y+36 x^{7} y^{2}+84 x^{6} y^{3}+126 x^{5} y^{4}} {+126 x^{4} y^{5}+84 x^{3} y^{6}+36 x^{2} y^{7}+9 x y^{8}+y^{9}}\end{array}\)

35. \(\begin{array}{l}{x^{8}-8 x^{7} y+28 x^{6} y^{2}-56 x^{5} y^{3}+70 x^{4} y^{4}} {-56 x^{3} y^{5}+28 x^{2} y^{6}-8 x y^{7}+y^{8}}\end{array}\)

Вправа\(\PageIndex{7}\)

Визначте факторіали цілих чисел\(5, 10, 15, 20\), і\(25\). Що зростає швидше, загальна експоненціальна функція\(a_{n} = 10^{n}\) або факторіальна функція\(a_{n} = n!\)? Поясніть.
Досліджуйте та обговоріть історію біноміальної теореми.

Відповідь: 1. Відповідь може відрізнятися

Виноски

²⁵ Добуток всіх натуральних чисел менше або дорівнює заданому натуральному числу, що позначається\(n!\).

²⁶ Факторіал нуля визначається рівним\(1; 0! = 1\).

²⁷ Ціле число, яке обчислюється за формулою:\(\left( \begin{array}{l}{n} \\[4pt] {k}\end{array}\right)=\frac{n !}{k !(n-k) !}\)

²⁸ Описує алгебраїчне розширення біноміалів, піднятих до повноважень:\((x+y)^{n}=\sum_{k=0}^{n} \left( \begin{array}{l}{n} \\[4pt] {k}\end{array}\right) x^{n-k} y^{k}\).

²⁹ Трикутний масив чисел, які відповідають біноміальним коефіцієнтам.