7.5: Загальна стратегія факторингу поліномів
- Page ID
- 58760
До кінця цього розділу ви зможете:
- Розпізнайте та використовуйте відповідний метод для повного множника
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Фактор\(y^{2}-2 y-24\).
Якщо ви пропустили цю проблему, перегляньте Вправа 7.2.19. - Фактор\(3 t^{2}+17 t+10\).
Якщо ви пропустили цю проблему, перегляньте Вправа 7.3.28. - Фактор\(36 p^{2}-60 p+25\).
Якщо ви пропустили цю проблему, перегляньте Вправа 7.4.1. - Фактор\(5 x^{2}-80\).
Якщо ви пропустили цю проблему, перегляньте Вправа 7.4.31.
Розпізнайте та використовуйте відповідний метод для повного фактору полінома
Ви зараз ознайомилися з усіма методами факторингу, які вам знадобляться в даному курсі. (У наступному курсі алгебри до вашого репертуару буде додано більше методів.) На малюнку нижче узагальнено всі методи факторингу, які ми розглянули. Рисунок\(\PageIndex{1}\) окреслює стратегію, яку слід використовувати при факторингу поліномів.

- Чи існує найбільший загальний фактор?
- Фактор це поза.
- Поліном є біноміальним, триноміальним, або існує більше трьох членів?
- Якщо це біном:
це сума?- З квадратів? Суми квадратів не коефіцієнт.
- З кубиків? Використовуйте шаблон суми кубиків.
- З квадратів? Фактор як добуток кон'югатів.
- З кубиків? Використовуйте різницю кубиків візерунка.
- Якщо це триноміал:
це форма\(x^{2}+b x+c ?\)? Скасувати фольгу.
Це форми\(a x^{2}+b x+c\)?- Якщо aa та cc є квадратами, перевірте, чи відповідає він шаблону триноміального квадрата.
- Використовуйте метод проб і помилок або «ac».
- Якщо він містить більше трьох термінів:
скористайтеся методом групування.
- Якщо це біном:
- Перевірте.
- Чи повністю це враховується?
- Чи множиться множник до початкового многочлена?
Пам'ятайте, поліном повністю враховується, якщо, крім мономів, його фактори прості!
Фактор повністю:\(4 x^{5}+12 x^{4}\)
- Відповідь
-
\ (\ begin {масив} {lll}\ text {Чи є GCF? } &\ text {Так,} 4 x^ {4} & 4 x^ {5} +12 x^ {4}\\ text {Фактор з GCF.} & &4 x^ {4} (x+3)\\ text {У дужках це біноміал, a} &\\ text {триноміальний, або існує більше трьох термінів? } &\ text {Біноміальний.} &\\ quad\ text {Це сума? } &\ text {Так.}\\ quad\ text {З квадратів? З кубиків? } &\ text {No.}\\ text {Перевірте.}
\\\ quad\ text {Чи повністю враховано вираз? } &\ текст {Так.}\\ quad\ текст {Множення.}\\\ почати {масив} {l} {4 x^ {4} (x+3)}\\ {4 x^ {4}\ cdot x+4 x^ {4}\ cdot 3}\\ {4 x^ {5} +12 x^ {4}}\ галочка\ кінець {масив}}\)
Фактор повністю:\(3 a^{4}+18 a^{3}\)
- Відповідь
-
3\(a^{3}(a+6)\)
Фактор повністю:\(45 b^{6}+27 b^{5}\)
- Відповідь
-
9\(b^{5}(5 b+3)\)
Фактор повністю:\(12 x^{2}-11 x+2\)
- Відповідь
-
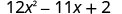
Чи є GCF? Ні. Це біноміальний, триноміальний, або
існує більше трьох термінів?Тримінал. Чи ідеальні квадрати a і c? Ні, а = 12,
не ідеальний квадрат.Використовуйте метод проб і помилок або метод «ac».
Тут ми будемо використовувати метод проб і помилок.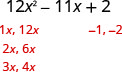
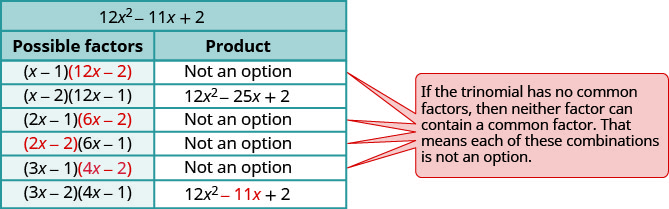
- Перевірте. \(\begin{array}{l}{(3 x-2)(4 x-1)} \\ {12 x^{2}-3 x-8 x+2} \\ {12 x^{2}-11 x+2 }\checkmark \end{array}\)
Фактор повністю:\(10 a^{2}-17 a+6\)
- Відповідь
-
\((5 a-6)(2 a-1)\)
Фактор повністю:\(8 x^{2}-18 x+9\)
- Відповідь
-
\((2 x-3)(4 x-3)\)
Фактор повністю:\(g^{3}+25 g\)
- Відповідь
-
\(\begin{array}{lll} \text { Is there a GCF? } & \text{Yes, g.} &g^{3}+25 g \\\text { Factor out the GCF. } & &g\left(g^{2}+25\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more than three terms? } &\text { Binomial. } & \\ \quad \text { Is it a sum? Of squares? } & \text { Yes. } & \text { Sums of squares are prime. } \\\text { Check. } \\ \\ \quad \text { Is the expression factored completely? } &\text { Yes. } \\ \quad \text { Multiply. } \\ \qquad \begin{array}{l}{g\left(g^{2}+25\right)} \\ {g^{3}+25 g }\checkmark \end{array} \end{array}\)
Фактор повністю:\(x^{3}+36 x\)
- Відповідь
-
\(x\left(x^{2}+36\right)\)
Фактор повністю:\(27 y^{2}+48\)
- Відповідь
-
3\(\left(9 y^{2}+16\right)\)
Фактор повністю:\(12 y^{2}-75\)
- Відповідь
-
\(\begin{array}{lll} \text { Is there a GCF? } & \text{Yes, 3.} &12 y^{2}-75 \\\text { Factor out the GCF. } & &3\left(4 y^{2}-25\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more than three terms? } &\text { Binomial. } & \\ \text { Is it a sum?} & \text { No. } & \\ \text { Is it a difference? Of squares or cubes? } &\text { Yes, squares. } & 3\left((2 y)^{2}-(5)^{2}\right) \\ \text { Write as a product of conjugates. } & &3(2 y-5)(2 y+5)\\\text { Check. } \\ \\ \text { Is the expression factored completely? } & \text{ Yes.}& \\ \text { Neither binomial is a difference of } \\ \text { squares. } \\ \text{ Multiply.} \\ \quad \begin{array}{l}{3(2 y-5)(2 y+5)} \\ {3\left(4 y^{2}-25\right)} \\ {12 y^{2}-75}\checkmark \end{array} \end{array}\)
Фактор повністю:\(16 x^{3}-36 x\)
- Відповідь
-
4\(x(2 x-3)(2 x+3)\)
Фактор повністю:\(27 y^{2}-48\)
- Відповідь
-
3\((3 y-4)(3 y+4)\)
Фактор повністю:\(4 a^{2}-12 a b+9 b^{2}\)
- Відповідь
-
Чи є GCF? Ні. 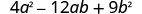
Це біноміальне, триноміальне, чи є
більше термінів?Триноміал с\(a\neq 1\). Але перший термін - це
ідеальний квадрат.Останній термін - ідеальний квадрат? Так. 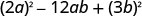
Чи підходить він до візерунка,\(a^{2}-2 a b+b^{2}\)? Так. 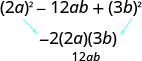
Напишіть його у вигляді квадрата. 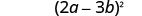
Перевірте свою відповідь. Чи повністю врахований вираз? Так. Біноміал - це не різниця квадратів. Помножити. \((2 a-3 b)^{2}\) \((2 a)^{2}-2 \cdot 2 a \cdot 3 b+(3 b)^{2}\) \(4 a^{2}-12 a b+9 b^{2} \checkmark\)
Фактор повністю:\(4 x^{2}+20 x y+25 y^{2}\)
- Відповідь
-
\((2 x+5 y)^{2}\)
Фактор повністю:\(9 m^{2}+42 m n+49 n^{2}\)
- Відповідь
-
\((3 m+7 n)^{2}\)
Фактор повністю:\(6 y^{2}-18 y-60\)
- Відповідь
-
\(\begin{array}{lll} \text { Is there a GCF? } & \text{Yes, 6.} &6 y^{2}-18 y-60 \\\text { Factor out the GCF. } & \text { Trinomial with leading coefficient } 1&6\left(y^{2}-3 y-10\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more terms? } & & \\ \text { "Undo' FOIL. } & 6(y\qquad )(y\qquad ) &6(y+2)(y-5) \\ \text { Check your answer. } \\ \text { Is the expression factored completely? } & & \text{ Yes.} \\ \text { Neither binomial is a difference of squares. } \\ \text { Multiply. } \\ \\\qquad \begin{array}{l}{6(y+2)(y-5)} \\ {6\left(y^{2}-5 y+2 y-10\right)} \\ {6\left(y^{2}-3 y-10\right)} \\ {6 y^{2}-18 y-60} \checkmark \end{array} \end{array}\)
Фактор повністю:\(8 y^{2}+16 y-24\)
- Відповідь
-
8\((y-1)(y+3)\)
Фактор повністю:\(5 u^{2}-15 u-270\)
- Відповідь
-
5\((u-9)(u+6)\)
Фактор повністю:\(24 x^{3}+81\)
- Відповідь
-
Чи є GCF? Так, 3. \(24 x^{3}+81\) Фактор це поза. 3\(\left(8 x^{3}+27\right)\) У дужках це біноміальне, триноміальне,
чи є більше трьох членів?Біноміальний. Це сума чи різниця? Сума. З квадратів або кубиків? Сума кубів. 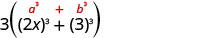
Напишіть його, використовуючи шаблон суми кубиків. 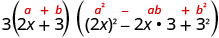
Чи повністю враховано вираз? Так. 3\((2 x+3)\left(4 x^{2}-6 x+9\right)\) Перевірка шляхом множення. Ми залишаємо чек вам.
Фактор повністю:\(250 m^{3}+432\)
- Відповідь
-
2\((5 m+6)\left(25 m^{2}-30 m+36\right)\)
Фактор повністю:\(81 q^{3}+192\)
- Відповідь
-
\(3(3q+4)\left(9q^{2}-12 q+16\right)\)
Фактор повністю:\(2 x^{4}-32\)
- Відповідь
-
\(\begin{array}{llc} \text { Is there a GCF? } & \text{Yes, 2.} &2 x^{4}-32 \\\text { Factor out the GCF. } & &2\left(x^{4}-16\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more than three terms? } & \text { Binomial. }& \\ \text { Is it a sum or difference? } &\text { Yes. }& \\\text { Of squares or cubes? } & \text { Difference of squares. } & 2\left(\left(x^{2}\right)^{2}-(4)^{2}\right) \\ \text { Write it as a product of conjugates. } & & 2\left(x^{2}-4\right)\left(x^{2}+4\right) \\ \text { The first binomial is again a difference of squares. } & & 2\left((x)^{2}-(2)^{2}\right)\left(x^{2}+4\right) \\ \text { Write it as a product of conjugates. } & & 2(x-2)(x+2)\left(x^{2}+4\right) \\ \text { Is the expression factored completely? } &\text { Yes. } & \\ \\ \text { None of these binomials is a difference of squares. } \\ \text { Check your answer. } \\ \text{ Multiply. }\\ \\ \qquad \qquad \begin{array}{l}{2(x-2)(x+2)\left(x^{2}+4\right)} \\ {2(x-2)(x+2)\left(x^{2}+4\right)} \\ {2(x-10)} \\ {2 x^{4}-32} \checkmark \end{array} \end{array}\)
Фактор повністю:\(4 a^{4}-64\)
- Відповідь
-
4\(\left(a^{2}+4\right)(a-2)(a+2)\)
Фактор повністю:\(7 y^{4}-7\)
- Відповідь
-
7\(\left(y^{2}+1\right)(y-1)(y+1)\)
Фактор повністю:\(3 x^{2}+6 b x-3 a x-6 a b\)
- Відповідь
-
\(\begin{array}{llc} \text { Is there a GCF? } & \text{Yes, 3.} &3 x^{2}+6 b x-3 a x-6 a b\\\text { Factor out the GCF. } & &3\left(x^{2}+2 b x-a x-2 a b\right)\\ \text { In the parentheses, is it a binomial, trinomial, } &\text { More than } 3 & \\ \text { or are there more terms? } &\text { terms. } & \\ \text { Use grouping. } & & \begin{array}{c}{3[x(x+2 b)-a(x+2 b)]} \\ {3(x+2 b)(x-a)}\end{array} \\ \text { Check your answer. } \\ \\ \text { Is the expression factored completely? Yes. } \\ \text { Multiply. } \\\qquad \qquad \begin{array}{l}{3(x+2 b)(x-a)} \\ {3\left(x^{2}-a x+2 b x-2 a b\right)} \\ {3 x^{2}-3 a x+6 b x-6 a b} \checkmark \end{array}\end{array}\)
Фактор повністю:\(6 x^{2}-12 x c+6 b x-12 b c\)
- Відповідь
-
6\((x+b)(x-2 c)\)
Фактор повністю:\(16 x^{2}+24 x y-4 x-6 y\)
- Відповідь
-
2\((4 x-1)(x+3 y)\)
Фактор повністю:\(10 x^{2}-34 x-24\)
- Відповідь
-
\(\begin{array}{llc} \text { Is there a GCF? } & \text{Yes, 2.} &10 x^{2}-34 x-24\\\text { Factor out the GCF. } & &2\left(5 x^{2}-17 x-12\right)\\ \text { In the parentheses, is it a binomial, trinomial, } &\text { Trinomial with } & \\ \text { or are there more than three terms? } &\space a \neq 1 & \\ \text { Use trial and error or the "ac" method. } & & 2\left(5 x^{2}-17 x-12\right) \\ & & 2(5 x+3)(x-4) \\ \text { Check your answer. Is the expression factored } \\\text { completely? Yes. }\\ \\ \text { Multiply. } \\ \qquad \begin{array}{l}{2(5 x+3)(x-4)} \\ {2\left(5 x^{2}-20 x+3 x-12\right)} \\ {2\left(5 x^{2}-17 x-12\right)} \\ {10 x^{2}-34 x-24}\checkmark \end{array}\end{array}\)
Фактор повністю:\(4 p^{2}-16 p+12\)
- Відповідь
-
4\((p-1)(p-3)\)
Фактор повністю:\(6 q^{2}-9 q-6\)
- Відповідь
-
3\((q-2)(2 q+1)\)
Ключові концепції
- Загальна стратегія факторингу поліномів див\(\PageIndex{1}\). Рис.
- Як зробити множинні поліноми
- Чи існує найбільший загальний фактор? Фактор це поза.
- Поліном є біноміальним, триноміальним, або існує більше трьох членів?
- Якщо це біном:
це сума?- З квадратів? Суми квадратів не коефіцієнт.
- З кубиків? Використовуйте шаблон суми кубиків.
- З квадратів? Фактор як добуток кон'югатів.
- З кубиків? Використовуйте різницю кубиків візерунка.
- Якщо це триноміал:
це форма\(x^{2}+b x+c\)? Скасувати фольгу.
Це форми\(a x^{2}+b x+c\)?- Якщо 'a' і 'c' є квадратами, перевірте, чи відповідає він триноміальному квадратному шаблону.
- Використовуйте метод проб і помилок або «ac».
- Якщо він містить більше трьох термінів:
скористайтеся методом групування.
- Якщо це біном:
- Перевірте. Чи повністю це враховується? Чи множиться множник до початкового многочлена?
