Глава 5 Огляд вправ
- Page ID
- 58693
Глава 5 Огляд вправ
Розв'язуйте системи рівнянь за допомогою графіків
Визначте, чи є впорядкована пара розв'язком системи рівнянь.
У наступних вправах визначте, чи є наступні пункти розв'язками заданої системи рівнянь.
\(\left\{\begin{array}{l}{x+3 y=-9} \\ {2 x-4 y=12}\end{array}\right.\)
- (−3, −2)
- (0, −3)
- Відповідь
-
- ні
- так
\(\left\{\begin{array}{l}{x+y=8} \\ {y=x-4}\end{array}\right.\)
- (6,2)
- (9, −1)
Розв'язуйте систему лінійних рівнянь шляхом графікування
У наступних вправах розв'яжіть наступні системи рівнянь шляхом побудови графіків.
\(\left\{\begin{array}{l}{3 x+y=6} \\ {x+3 y=-6}\end{array}\right.\)
- Відповідь
-
(3, −3)
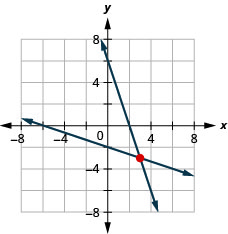
\(\left\{\begin{array}{l}{y=x-2} \\ {y=-2 x-2}\end{array}\right.\)
\(\left\{\begin{array}{l}{2 x-y=6} \\ {y=4}\end{array}\right.\)
- Відповідь
-
(5,4)
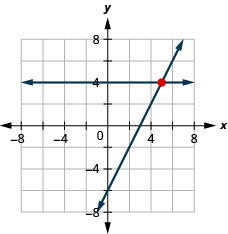
\(\left\{\begin{array}{l}{x+4 y=-1} \\ {x=3}\end{array}\right.\)
\(\left\{\begin{array}{l}{2 x-y=5} \\ {4 x-2 y=10}\end{array}\right.\)
- Відповідь
-
збігаються лінії
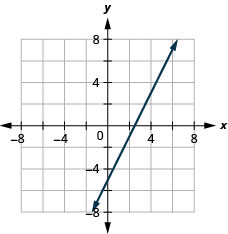
\(\left\{\begin{array}{l}{-x+2 y=4} \\ {y=\frac{1}{2} x-3}\end{array}\right.\)
Визначте кількість розв'язків лінійної системи
У наступних вправах без графіків визначають кількість розв'язків, а потім класифікують систему рівнянь.
\(\left\{\begin{array}{l}{y=\frac{2}{5} x+2} \\ {-2 x+5 y=10}\end{array}\right.\)
- Відповідь
-
нескінченно багато розв'язків, послідовна система, залежні рівняння
\(\left\{\begin{array}{l}{3 x+2 y=6} \\ {y=-3 x+4}\end{array}\right.\)
\(\left\{\begin{array}{l}{5 x-4 y=0} \\ {y=\frac{5}{4} x-5}\end{array}\right.\)
- Відповідь
-
відсутність розв'язків, непослідовна система, незалежні рівняння
\(\left\{\begin{array}{l}{y=-\frac{3}{4} x+1} \\ {6 x+8 y=8}\end{array}\right.\)
Розв'язування застосувань систем рівнянь методом графування
LaVelle робить глечик з кафе мокко. На кожну унцію шоколадного сиропу вона використовує п'ять унцій кави. Скільки унцій шоколадного сиропу і скільки унцій кави їй потрібно, щоб зробити 48 унцій кави мокко?
- Відповідь
-
LaVelle потрібно 8 унцій шоколадного сиропу і 40 унцій кави.
Елі робить партійний мікс, який містить кренделі та шекс. На кожну чашку кренделі він використовує три чашки шексу. Скільки чашок кренделів і скільки чашок шекс йому потрібно, щоб зробити 12 чашок партійної суміші?
Розв'язування систем рівнянь шляхом заміщення
Розв'язувати систему рівнянь шляхом заміщення
У наступних вправах розв'яжіть системи рівнянь шляхом підстановки.
\(\left\{\begin{array}{l}{3 x-y=-5} \\ {y=2 x+4}\end{array}\right.\)
- Відповідь
-
(−1,2)
\(\left\{\begin{array}{l}{3 x-2 y=2} \\ {y=\frac{1}{2} x+3}\end{array}\right.\)
\(\left\{\begin{array}{l}{x-y=0} \\ {2 x+5 y=-14}\end{array}\right.\)
- Відповідь
-
(−2, −2)
\(\left\{\begin{array}{l}{y=-2 x+7} \\ {y=\frac{2}{3} x-1}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=-5 x} \\ {5 x+y=6}\end{array}\right.\)
- Відповідь
-
немає рішення
\(\left\{\begin{array}{l}{y=-\frac{1}{3} x+2} \\ {x+3 y=6}\end{array}\right.\)
Розв'язування застосувань систем рівнянь заміщенням
У наступних вправах переведіть на систему рівнянь і розв'яжіть.
Сума двох чисел дорівнює 55. Одне число на 11 менше іншого. Знайдіть цифри.
- Відповідь
-
Цифри - 22 і 33.
Периметр прямокутника дорівнює 128. Довжина на 16 більше ширини. Знайдіть довжину і ширину.
Міра одного з малих кутів прямокутного трикутника в 2 менше, ніж в 3 рази міра іншого малого кута. Знайдіть міру обох кутів.
- Відповідь
-
Заходи - 23 градуси і 67 градусів.
Габріела працює в страховій компанії, яка виплачує їй зарплату в розмірі 32 000 доларів плюс комісія в розмірі 100 доларів за кожен поліс, який вона продає. Вона розглядає можливість зміни роботи на компанію, яка б заплатила зарплату в розмірі 40 000 доларів плюс комісія в розмірі 80 доларів за кожен проданий поліс. Скільки полісів потрібно було б продати Габріелі, щоб загальна оплата була однаковою?
Розв'язувати системи рівнянь шляхом ліквідації
Розв'яжіть систему рівнянь шляхом усунення У наступних вправах розв'яжіть системи рівнянь шляхом усунення.
\(\left\{\begin{array}{l}{x+y=12} \\ {x-y=-10}\end{array}\right.\)
- Відповідь
-
(1,11)
\(\left\{\begin{array}{l}{4 x+2 y=2} \\ {-4 x-3 y=-9}\end{array}\right.\)
\(\left\{\begin{array}{l}{3 x-8 y=20} \\ {x+3 y=1}\end{array}\right.\)
- Відповідь
-
(4, −1)
\(\left\{\begin{array}{l}{3 x-2 y=6} \\ {4 x+3 y=8}\end{array}\right.\)
\(\left\{\begin{array}{l}{9 x+4 y=2} \\ {5 x+3 y=5}\end{array}\right.\)
- Відповідь
-
(−2,5)
\(\left\{\begin{array}{l}{-x+3 y=8} \\ {2 x-6 y=-20}\end{array}\right.\)
Розв'язування застосувань систем рівнянь шляхом ліквідації
У наступних вправах переведіть на систему рівнянь і розв'яжіть.
Сума двох чисел дорівнює −90. Їх відмінність становить 16. Знайдіть цифри.
- Відповідь
-
Числа: −37 та −53.
Омар щодня зупиняється в магазині пончиків по дорозі на роботу. Минулого тижня у нього було 8 пончиків та 5 капучіно, що дало йому загалом 3000 калорій. Цього тижня у нього було 6 пончиків та 3 капучіно, що загалом склало 2160 калорій. Скільки калорій в одному пончику? Скільки калорій в одному капучино?
Виберіть найбільш зручний метод розв'язання системи лінійних рівнянь
У наступних вправах визначитеся, чи зручніше буде вирішувати систему рівнянь шляхом підстановки або усунення.
\(\left\{\begin{array}{l}{6 x-5 y=27} \\ {3 x+10 y=-24}\end{array}\right.\)
- Відповідь
-
усунення
\(\left\{\begin{array}{l}{y=3 x-9} \\ {4 x-5 y=23}\end{array}\right.\)
Розв'язуйте програми з системами рівнянь
Перекласти на систему рівнянь
У наступних вправах переведіть на систему рівнянь. Чи не вирішуйте систему.
Сума двох чисел дорівнює −32. Одне число на два менше, ніж удвічі більше іншого. Знайдіть цифри.
- Відповідь
-
\(\left\{\begin{array}{l}{x+y=-32} \\ {x=2 y-2}\end{array}\right.\)
Чотири рази більше числа плюс тричі друге число −9. Двічі перше число плюс друге число - три. Знайдіть цифри.
Минулого місяця Джим і Деббі заробили $7200. Деббі заробила на 1,600 доларів більше, ніж заробив Джим. Скільки кожен заробив?
- Відповідь
-
\(\left\{\begin{array}{l}{j+d=7200} \\ {d=j+1600}\end{array}\right.\)
Анрі має $24,000 інвестували в акції та облігації. Сума в акціях на 6000 доларів більше, ніж втричі перевищує суму в облігаціях. Скільки коштує кожна інвестиція?
Розв'язуйте програми прямого перекладу
У наступних вправах переведіть на систему рівнянь і розв'яжіть.
Пем на 3 роки старша за свою сестру, січня, сума їхнього віку становить 99 років. Знайдіть їх вік.
- Відповідь
-
Пем 51 рік, а Яну - 48.
Моллі хоче посадити 200 цибулин у своєму саду. Вона хоче всіх ірисів і тюльпанів. Вона хоче посадити в три рази більше тюльпанів, ніж ірисів. Скільки ірисів і скільки тюльпанів їй посадити?
Вирішити додатки геометрії
У наступних вправах переведіть на систему рівнянь і розв'яжіть.
Різниця двох додаткових кутів становить 58 градусів. Знайдіть міри кутів.
- Відповідь
-
Заходи - 119 градусів і 61 градус.
Два кута взаємодоповнюють один одного. Міра більшого кута в п'ять більше чотирьох разів перевищує міру меншого кута. Знайдіть міри обох кутів.
Бекка висить квіткову гірлянду 28 футів з двох сторін і зверху перголи, щоб підготуватися до весілля. Висота на чотири фути менше ширини. Знайдіть висоту і ширину перголи.
Відповідь
-
Пергола має висоту 8 футів і ширину 12 футів.
Периметр міського прямокутного парку становить 1428 футів. Довжина на 78 футів більше, ніж в два рази більше ширини. Знайдіть довжину і ширину парку.
Вирішити рівномірні програми руху
У наступних вправах переведіть на систему рівнянь і розв'яжіть.
Шейла і Ленор їхали в будинок своєї бабусі. Ленор пішов через годину після Шейли. Шейла їхала зі швидкістю 45 миль/год, а Ленор їхав зі швидкістю 60 миль/год. Скільки часу знадобиться Ленору, щоб наздогнати Шейлу?
- Відповідь
-
На це піде Леноре 3 години.
Боб пішов з дому, катаючись на своєму велосипеді зі швидкістю 10 миль на годину, щоб відправитися до озера. Шеріл, його дружина, поїхала через 45 хвилин (\(\frac{3}{4}\)годину), керуючи своїм автомобілем зі швидкістю 25 миль на годину. Скільки часу знадобиться Шеріл, щоб наздогнати Боба?
Маркус може проїхати свій човен 36 миль вниз по річці протягом трьох годин, але займає чотири години, щоб повернутися вгору за течією. Знайти швидкість човна в негазованій воді і швидкість течії.
- Відповідь
-
Швидкість катера - 10,5 миль/год. Швидкість течії - 1,5 миль/год.
Пасажирський літак може пролетіти 804 миль за 2 години з попутним вітром, але лише 776 миль за 2 години в зустрічному вітрі. Знайдіть швидкість струменя в нерухомому повітрі і швидкість вітру.
Розв'язування сумішшних застосувань з системами рівнянь
Вирішити додатки суміші
У наступних вправах переведіть на систему рівнянь і розв'яжіть.
Лінн заплатила в цілому 2780 доларів за 261 квиток в театр. Студентські квитки коштують 10 доларів, а дорослі - 15 доларів. Скільки студентських квитків і скільки квитків для дорослих купила Лінн?
- Відповідь
-
Лінн купила 227 студентських квитків і 34 дорослі квитки.
У Priam є копійки і копійки в підстаканнику в своїй машині. Загальна вартість монет становить $4.21. Кількість копійок в три менше, ніж в чотири рази перевищує кількість копійок. Скільки копійок і скільки копійок в чашці?
Юмі хоче зробити 12 чашок партійної суміші, використовуючи цукерки та горіхи. Її бюджет вимагає, щоб партійна суміш коштувала їй $1,29 за чашку. Цукерки становлять $2,49 за чашку, а горіхи - 0,69 долара за чашку. Скільки чашок цукерок і скільки чашок горіхів вона повинна вживати?
- Відповідь
-
Юмі слід використовувати 4 чашки цукерок і 8 чашок горіхів.
Вченому потрібно 70 літрів 40% -ного розчину спирту. У нього є 30% і 60% розчин в наявності. Скільки літрів 30% і скільки літрів 60% розчинів він повинен змішувати, щоб вийшов 40% розчин?
Вирішити інтереси додатків
У наступних вправах переведіть на систему рівнянь і розв'яжіть.
Джек має $12,000, щоб інвестувати і хоче заробляти 7,5% відсотків на рік. Він покладе частину грошей на ощадний рахунок, який заробляє 4% на рік, а решту на рахунок CD, який заробляє 9% на рік. Скільки грошей він повинен покласти на кожен рахунок?
- Відповідь
-
Джек повинен покласти $3600 в економію і $8400 на компакт-диск.
Коли вона закінчить коледж, Лінда заборгуватиме 43 000 доларів студентських кредитів. Процентна ставка за федеральними кредитами становить 4,5%, а ставка по кредитах приватного банку - 2%. Загальний відсоток, який вона заборгувала за один рік, становив 1585 доларів. Яка сума кожного кредиту?
Графічні системи лінійних нерівностей
Визначити, чи є впорядкована пара розв'язком системи лінійних нерівностей
У наступних вправах визначте, чи є кожна впорядкована пара рішенням системи.
\(\left\{\begin{array}{l}{4 x+y>6} \\ {3 x-y \leq 12}\end{array}\right.\)
- (2, −1)
- (3, −2)
- Відповідь
-
- так
- ні
\(\left\{\begin{array}{l}{y>\frac{1}{3} x+2} \\ {x-\frac{1}{4} y \leq 10}\end{array}\right.\)
- (6,5)
- (15,8)
Розв'язувати систему лінійних нерівностей за допомогою графіків
У наступних вправах вирішуйте кожну систему за допомогою графіків.
\(\left\{\begin{array}{l}{y<3 x+1} \\ {y \geq-x-2}\end{array}\right.\)
- Відповідь
-
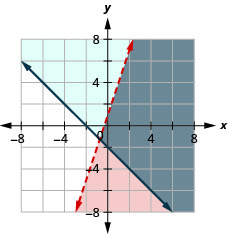
\(\left\{\begin{array}{l}{x-y>-1} \\ {y<\frac{1}{3} x-2}\end{array}\right.\)
\(\left\{\begin{array}{l}{2 x-3 y<6} \\ {3 x+4 y \geq 12}\end{array}\right.\)
- Відповідь
-
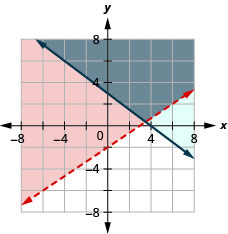
\(\left\{\begin{array}{l}{y \leq-\frac{3}{4} x+1} \\ {x \geq-5}\end{array}\right.\)
\(\left\{\begin{array}{l}{x+3 y<5} \\ {y \geq-\frac{1}{3} x+6}\end{array}\right.\)
- Відповідь
-
Немає рішення
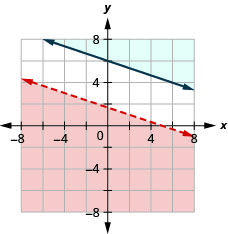
\(\left\{\begin{array}{l}{y \geq 2 x-5} \\ {-6 x+3 y>-4}\end{array}\right.\)
Розв'язування застосувань систем нерівностей
У наступних вправах переведіть на систему нерівностей і вирішуйте.
Роксана виготовляє браслети та намиста і продає їх на фермерському ринку. Вона продає браслети по 12 доларів кожен, а намиста по 18 доларів кожен. На ринку в наступні вихідні у неї буде місце для демонстрації не більше 40 штук, а їй потрібно продати мінімум $500 вартістю, щоб заробити прибуток.
- Напишіть систему нерівностей для моделювання цієї ситуації.
- Графік системи.
- Чи повинна вона відображати 26 браслетів і 14 намиста?
- Чи повинна вона відображати 39 браслетів і 1 намисто?
- Відповідь
-
- \(\left\{\begin{array}{l}{b+n \leq 40} \\ {12 b+18 n \geq 500}\end{array}\right.\)
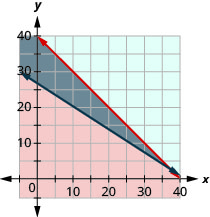
3. так
4. ні
Енні має бюджет у розмірі 600 доларів на придбання книг у м'якій обкладинці та книг у твердій палітурці для її класу. Вона хоче, щоб кількість обкладинки в твердій обкладинці була щонайменше на 5 більше, ніж втричі більше, ніж кількість книг у м'якій обкладинці. Книги в м'якій обкладинці коштують 4 долари, а книги в твердій обкладинці коштують 15 доларів кожна.
- Напишіть систему нерівностей для моделювання цієї ситуації.
- Графік системи.
- Чи може вона придбати 8 книг у м'якій обкладинці та 40 книг у твердій палітурці?
- Чи може вона придбати 10 книг у м'якій обкладинці та 37 книг у твердій палітурці?
Практика Тест
\(\left\{\begin{array}{l}{x-4 y=-8} \\ {2 x+5 y=10}\end{array}\right.\)
- (0,2)
- (4,3)
- Відповідь
-
- так
- ні
У наступних вправах вирішуйте наступні системи за допомогою графіків.
\(\left\{\begin{array}{l}{x-y=5} \\ {x+2 y=-4}\end{array}\right.\)
\(\left\{\begin{array}{l}{x-y>-2} \\ {y \leq 3 x+1}\end{array}\right.\)
- Відповідь
-
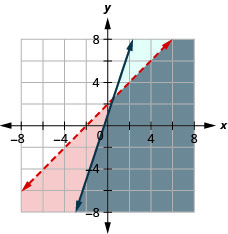
У наступних вправах вирішуйте кожну систему рівнянь. Використовують або заміщення, або усунення.
\(\left\{\begin{array}{l}{3 x-2 y=3} \\ {y=2 x-1}\end{array}\right.\)
\(\left\{\begin{array}{l}{x+y=-3} \\ {x-y=11}\end{array}\right.\)
- Відповідь
-
(4, −7)
\(\left\{\begin{array}{l}{4 x-3 y=7} \\ {5 x-2 y=0}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=-\frac{4}{5} x+1} \\ {8 x+10 y=10}\end{array}\right.\)
- Відповідь
-
нескінченно багато рішень
\(\left\{\begin{array}{l}{2 x+3 y=12} \\ {-4 x+6 y=-16}\end{array}\right.\)
У наступних вправах переведіть на систему рівнянь і розв'яжіть.
Сума двох чисел дорівнює −24. Одне число на 104 менше іншого. Знайдіть цифри.
- Відповідь
-
Цифри 40 і 64
Рамон хоче посадити огірки і помідори на своєму городі. У нього місце для 16 рослин, і він хоче посадити в три рази більше огірків, ніж помідорів. Скільки огірків і скільки томатів він повинен посадити?
Два кута взаємодоповнюють один одного. Міра більшого кута в шість більше ніж в два рази перевищує міру меншого кута. Знайдіть міри обох кутів.
- Відповідь
-
Міри кутів - 28 градусів і 62 градуси.
У понеділок Ленс біг 30 хвилин і плавав 20 хвилин. Його фітнес-додаток сказав йому, що він спалив 610 калорій. У середу фітнес-додаток сказав йому, що він спалив 695 калорій, коли бігав 25 хвилин і плавав 40 хвилин. Скільки калорій він спалив за одну хвилину бігу? Скільки калорій він спалив за одну хвилину плавання?
Кеті пішла додому, щоб дійти до торгового центру, швидко йшовши зі швидкістю 4 милі на годину. Її сестра Еббі пішла з дому через 15 хвилин і їхала на велосипеді до торгового центру зі швидкістю 10 миль на годину. Скільки часу знадобиться Еббі, щоб наздогнати Кеті?
- Відповідь
-
Це займе\(\frac{1}{6}\) у Кеті годину (або 10 хвилин)
Це займає 5\(\frac{1}{2}\) годин для літака, щоб пролетіти 2475 миль з зустрічним вітром від Сан-Хосе, Каліфорнія до Ліху, Гаваї. Зворотний рейс з Ліху в Сан-Хосе з попутним вітром займає 5 годин. Знайдіть швидкість струменя в нерухомому повітрі і швидкість вітру.
Ліз заплатила 160 доларів за 28 квитків, щоб відвезти військо Брауні до наукового музею. Дитячі квитки коштують 5 доларів, а дорослі - 9 доларів. Скільки дитячих квитків і скільки дорослих квитків купила Ліз?
- Відповідь
-
Ліз купила 23 дитячих квитка і 5 дорослих квитків.
Фармацевту потрібно 20 літрів 2% сольового розчину. У нього є 1% і 5% розчин в наявності. Скільки літрів 1% і скільки літрів 5% розчинів вона повинна змішувати, щоб вийшов 2% розчин?
Переведіть на систему нерівностей і вирішуйте.
Енді хоче витратити не більше 50 доларів на частування Хеллоуїна. Вона хоче купити цукерки, які коштують $1 кожен і льодяники, які коштують $0,50 кожен, і вона хоче, щоб кількість льодяників була принаймні втричі більше кількості цукеркових батончиків.
- Напишіть систему нерівностей для моделювання цієї ситуації.
- Графік системи.
- Чи може вона купити 20 батончиків і 70 льодяників?
- Чи може вона купити 15 батончиків і 65 льодяників?
- Відповідь
-
- \(\left\{\begin{array}{l}{C+0.5 L \leq 50} \\ {L \geq 3 C}\end{array}\right.\)
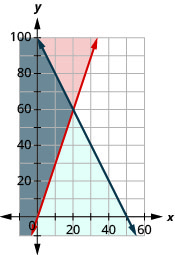
3. №
4. Так
