2.4: Розв'язок раціональних нерівностей за допомогою графіків

У попередньому розділі ми бачили, як розв'язати поліноміальні нерівності за допомогою графіків. У цьому розділі ми будемо використовувати подібні методи для вирішення раціональних нерівностей. Раціональні нерівності передбачають співвідношення многочленів або дробів. Оскільки ці типи задач включають дроби, графіки функцій, з якими ми працюємо, матимуть те, що відомі як асимптоти. Це слово походить від грецького кореня, пов'язаного з двома рядками, які дуже близько один до одного, але ніколи не зустрічаються.

Вертикальні асимптоти графа з'являться в місцях, де вихідний вираз має нульовий знаменник. Це означає, що функція не визначена в цих$x$ значеннях, і тому, замість того, щоб мати$y$ значення в цій точці, графік має асимптоту.

Приклад
Нижче наведено графік функції$y=\frac{x+2}{x-1}$

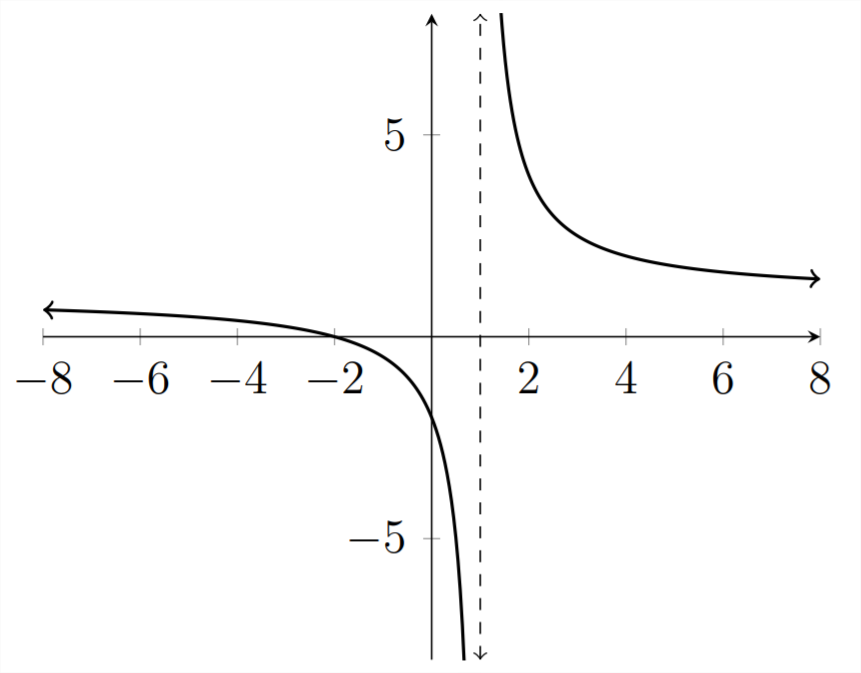
Замість того, щоб мати$y$ значення в точці$x=1$, де пунктирна лінія вказує асимптоту, де функція не визначена. У попередньому розділі ми були зацікавлені в пошуку коренів функції, оскільки це місця, де$y=0,$ і можуть бути точками поділу між тим, де$y$ значення більше нуля$(y>0)$ і де$y$ значення менше нуля$(y<0)$

Важливість асимптотів при аналізі раціональних функцій полягає в тому, що, як і коріння, вони представляють$x$ значення, які можуть бути точками поділу між де$y>0$ і де$y<0$

Приклад
Розв'яжіть задану нерівність.
$\frac{2}{x-3}>0$
Спочатку розглядаємо графік:

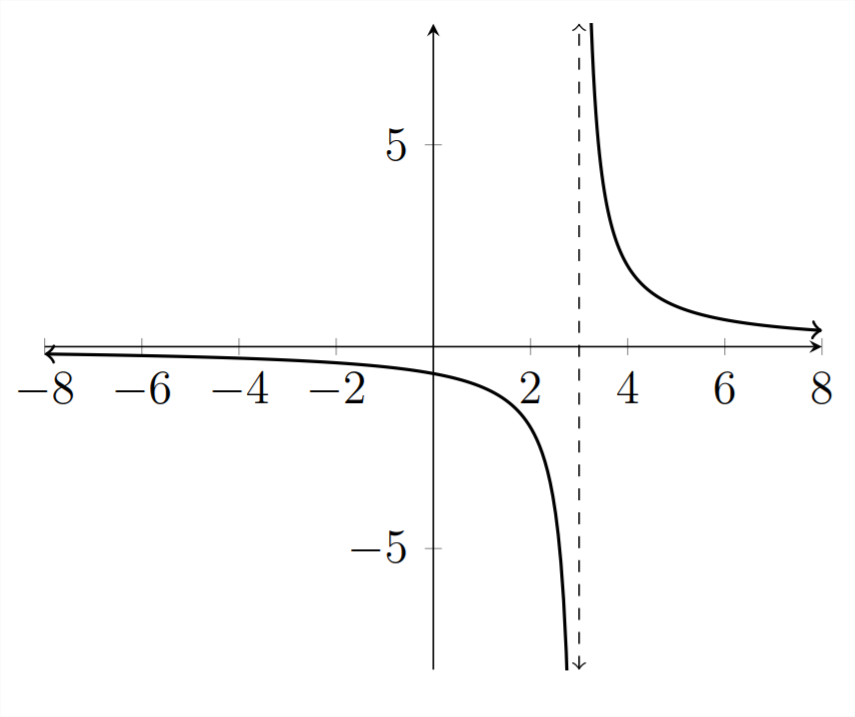
Зверніть увагу, що асимптота для цього графіка відбувається за значенням,$x=3,$ оскільки це$x$ значення, яке створює нульовий знаменник. Також зверніть увагу, що$y$ значення переходять від негативного до позитивного через асимптоту.

Для цієї функції немає коренів, оскільки немає$x$ значень, які роблять$y=0$ Для дробу нуль чисельник повинен дорівнювати нулю. У цьому прикладі чисельник дорівнює 2 і жодне значення не$x$ зробить його рівним нулю. Тому єдиною можливою точкою поділу на графіку є$x=3,$ і рішення нерівності$x>3$

Приклад
Розв'яжіть задану нерівність.
$\frac{x-2}{x-3}>0$

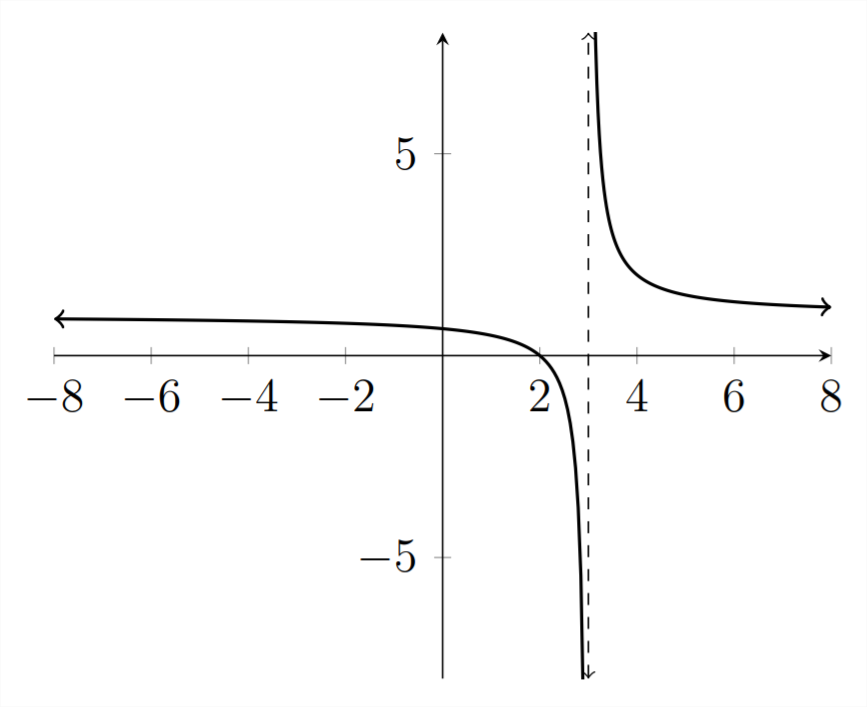
У цій нерівності, є знову асимптота в$x=3,$ але є також корінь на значення,$x=2,$ тому що коли$x=2 . y=\frac{2-2}{2-3}=\frac{0}{-1}=0 .$ Таким чином, ми маємо дві точки ділення, щоб розглянути,$x=2$ і$x=3 .$ Ми можемо бачити з графіка, що $y>0$для$x<2$ або$x>3,$ так, що це рішення даної нерівності.

Приклад
Розв'яжіть задану нерівність.
$\frac{x^{2}-2}{x-3}>0$
У цій задачі ми маємо ту саму асимптоту, що і попередні дві задачі:$x=$
3. Однак в цій нерівності є два корені, тому що є два$x$ значення, які роблять чисельник рівним нулю.
$x^{2}-2=0$означає, що$x^{2}=2$ і$x=\pm \sqrt{2} \approx \pm 1.414$
Ми можемо бачити ці корені на графіку.

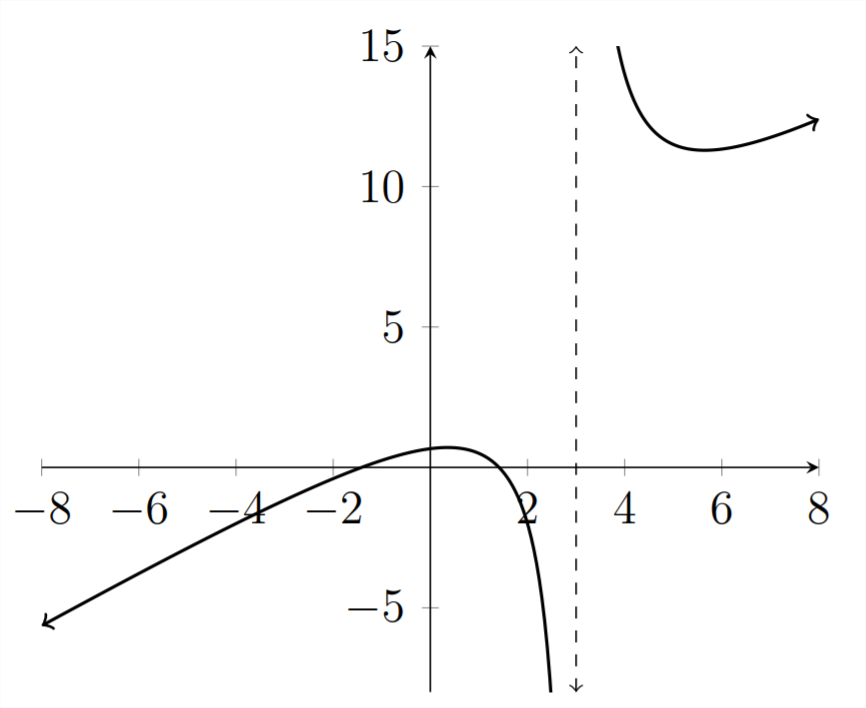
На графіку вище, ми можемо побачити асимптоту в$x=3$ і два корені в$x \approx 1.414,-1.414$
$x$ Значення,$y>0$ які роблять$-1.414<x<1.414$ або$x>3$

Приклад
Розв'яжіть задану нерівність.
$\frac{x-2}{x^{2}-3}>0$

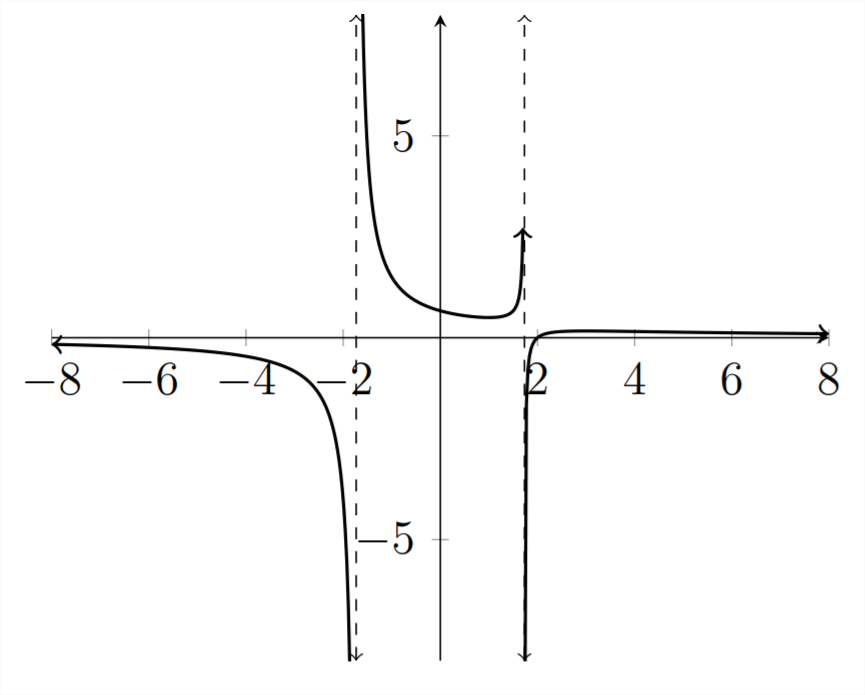
Коріння для цієї функції - це$x$ значення, які роблять чисельник рівним нулю:
$x-2=0,$ отже,$x=2,$ і ми можемо побачити цей корінь на графіку.

Асимптотами для функції є$x$ значення, які роблять знаменник рівним
нулю:
$x^{2}-3=0$ означає, що$x^{2}=3$ і$x=\pm \sqrt{3} \approx \pm 1.732$

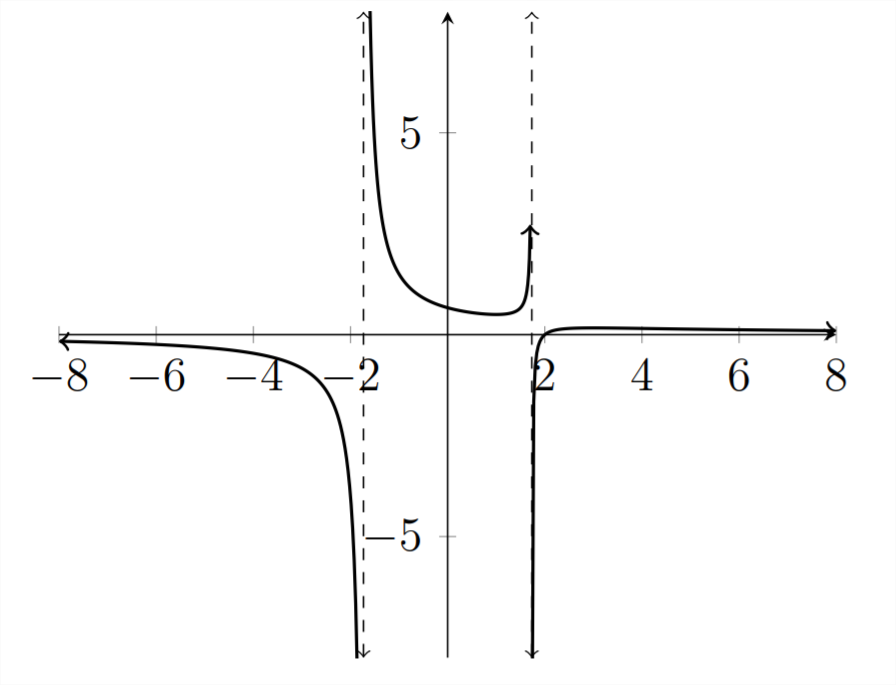
Тому розв'язком даної нерівності є:
$-1.732<x<1.732$ АБО$x>2$
Приклад
Розв'яжіть задану нерівність
$\frac{5 x+1}{x^{2}+3 x-4}<0$

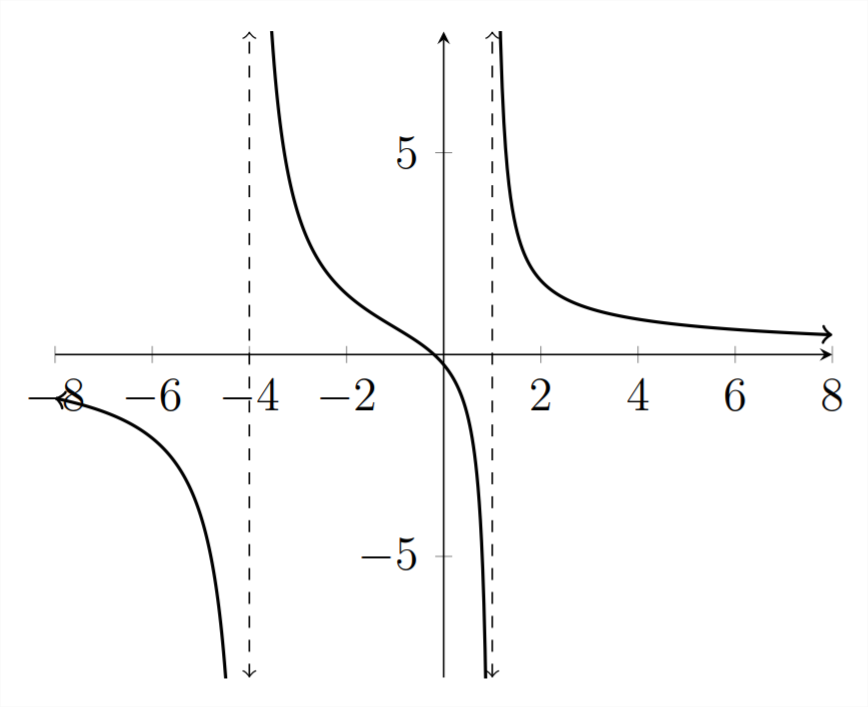
Коріння
$5 x+1=0$
$5 x=-1$
$x=-0.2=-\frac{1}{5}$
асимптотів
$x^{2}+3 x-4=0$
$(x+4)(x-1)=0$
$x=-4,1$

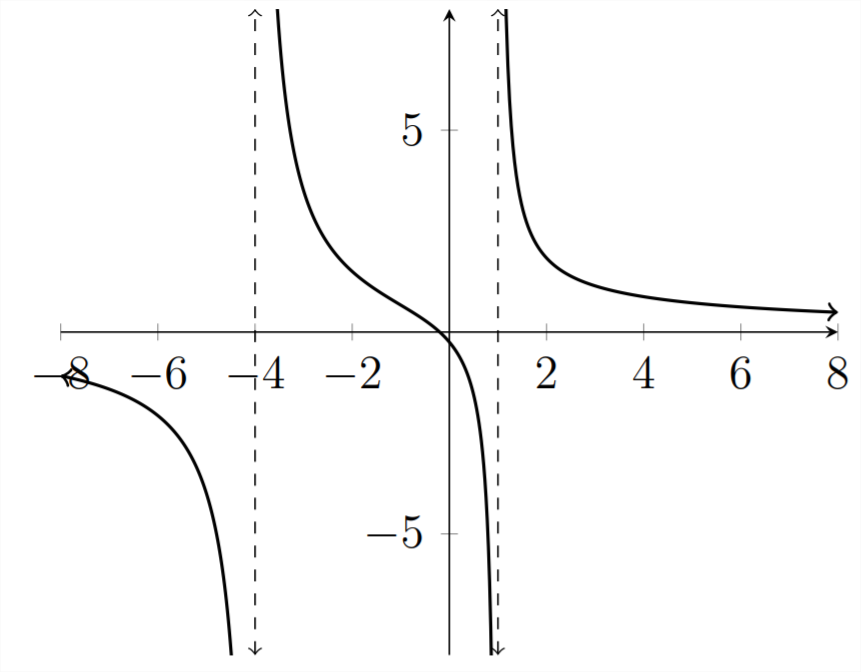
Якщо ми поєднаємо алгебраїчний аналіз вище з тим, що ми бачимо на графіку, то ми знаємо, що точки поділу, важливі для вирішення цієї нерівності, знаходяться в$x=-4,-0.2,1 .$ інтервалах, де$y$ значення менше нуля$x<-4$$\mathrm{OR}-0.2<x<1$

Приклад
$\frac{x^{2}+2 x-1}{x^{2}+7 x+5} \leq 0$

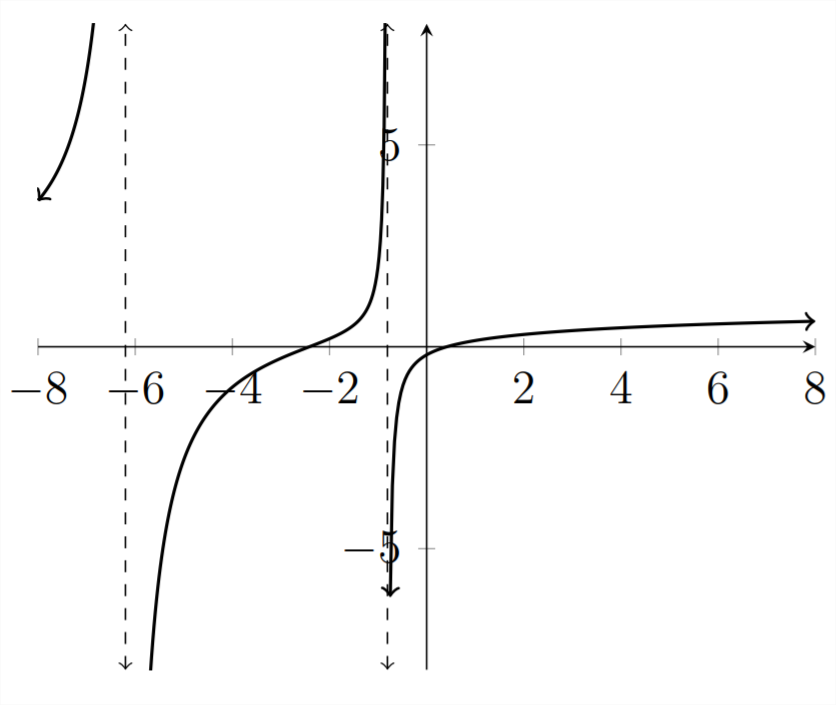
Коріння

\ [\ begin {масив} {l}
x^ {2} +2 x-1 = 0\\
x\ приблизно 2.414,0.414
\ end {масив}
\]
Асимптоти
$x^{2}+7 x+5=0$
\ [
x\ approx-6.193, -0.807
\]
Ми бачимо, що точками ділення, важливими для розв'язання нерівності, є Інтервали, де$y$ значення менше або рівні нулю$x \approx-6.193,-2.414,-0.807,0.414 .$ $-6.193 \leq x \leq-2.414$АБО$-0.807 \leq x \leq 0.414$

Вправи 2.4
Розв'яжіть кожну нерівність.
1)$\quad \frac{x+4}{x^{2}-8 x+12}>0$
2)$\quad \frac{2 x+3}{x^{2}-2 x-35}<0$
3)$\quad \frac{x^{2}-5 x-14}{x^{2}+3 x-10}<0$
4)$\quad \frac{2 x^{2}-x-3}{x^{2}+10 x+16}>0$
5)$\quad \frac{3 x+2}{x^{2}+x-5}<0$
6)$\quad \frac{x^{2}+2 x+5}{x^{2}-3 x-7}>0$
7)$\quad \frac{x^{3}+9}{x^{2}+x-1}>0$
8)$\quad \frac{x^{3}+9}{x^{2}+x+1}>0$

Вирішити кожну нерівність.
9)$\quad \frac{x^{2}-2 x-9}{3 x+11}>0$
10)$\quad \frac{x^{2}+4 x+3}{2 x+1}<0$
11)$\quad \frac{x^{2}+x-5}{x^{2}-x-6}>0$
12)$\quad \frac{x^{3}+2}{x^{2}-2}>0$
13)$\quad \frac{x^{2}+2 x-7}{x^{2}+3 x-6}<0$
14)$\quad \frac{2 x-x^{2}}{x^{2}-4 x+6}<0$
15)$\quad \frac{x^{2}-7}{x^{2}+5 x-1}<0$
16)$\quad \frac{x-5}{3 x^{2}-2 x-3}>0$