5.6: Нулі поліноміальних функцій

Last updated
Save as PDF

Page ID: 59615

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Оцінити многочлен за допомогою теореми про залишок.
Використовуйте теорему фактора для розв'язання поліноміального рівняння.
Використовуйте теорему про раціональний нуль, щоб знайти раціональні нулі.
Знайти нулі поліноміальної функції.
Використовуйте теорему лінійної факторизації для пошуку поліномів із заданими нулями.
Використовуйте правило знаків Декарта.
Розв'язування реальних застосувань поліноміальних рівнянь

Нова пекарня пропонує прикрашені листові торти для дитячих днів народження та інших урочистих випадків. Пекарня хоче, щоб обсяг невеликого пирога становив 351 кубічний дюйм. Торт у формі прямокутної суцільної форми. Вони хочуть, щоб довжина торта була на чотири сантиметри довшою, ніж ширина торта, а висота пирога - одна третина ширини. Якими повинні бути розміри форми для кексу?

Цю задачу можна вирішити, написавши кубічну функцію і розв'язавши кубічне рівняння для обсягу пирога. У цьому розділі ми обговоримо різноманітні інструменти для написання поліноміальних функцій і розв'язання поліноміальних рівнянь.

Оцінка полінома з використанням теореми про залишок

В останньому розділі ми дізналися, як ділити многочлени. Тепер ми можемо використовувати поліноміальне ділення для оцінки поліномів за допомогою теореми про залишок. Якщо многочлен розділити на$x–k$, залишок можна швидко знайти, оцінивши поліноміальну функцію при$k$, тобто$f(k)$. Давайте пройдемося доказом теореми.

Нагадаємо, що Алгоритм поділу стверджує, що, враховуючи поліноміальний дивіденд$f(x)$ і ненульовий поліноміальний дільник,$d(x)$ де ступінь менше або дорівнює ступеня$f(x)$, існують унікальні поліноми$q(x)$ і$r(x)$ такі, що$d(x)$

\[f(x)=d(x)q(x)+r(x) \nonumber\]

Якщо дільник,$d(x)$, є$x−k$, це набуває вигляду

\[f(x)=(x−k)q(x)+r \nonumber\]

Так як дільник$x−k$

лінійна, залишок буде постійною,$r$. І, якщо ми оцінюємо це для$x=k$, у нас є

\[\begin{align*} f(k)&=(k−k)q(k)+r \\[4pt] &=0{\cdot}q(k)+r \\[4pt] &=r \end{align*}\]

Іншими словами,$f(k)$ це залишок, отриманий$f(x)$ діленням на$x−k$.

Теорема про залишок

Якщо многочлен$f(x)$ ділиться на$x−k$, то залишок - це значення$f(k)$.

$альт$ Дано поліноміальну функцію$f$, оцінюють$f(x)$ за$x=k$ допомогою теореми про залишок.

Використовуйте синтетичне ділення, щоб розділити многочлен на$x−k$.
Залишок - це значення$f(k)$.

Приклад$\PageIndex{1}$: Using the Remainder Theorem to Evaluate a Polynomial

Використовуйте теорему про залишок для оцінки$f(x)=6x^4−x^3−15x^2+2x−7$ в$x=2$.

Рішення

Щоб знайти залишок за допомогою теореми про залишок, використовуйте синтетичне ділення, щоб розділити многочлен на$x−2$.

\[ 2 \begin{array}{|ccccc} \; 6 & −1 & −15 & 2 & −7 \\ \text{} & 12 & 22 & 14 & 32 \\ \hline \end{array} \\ \begin{array}{ccccc} 6 & 11 & \; 7 & \;\;16 & \;\; 25 \end{array} \]

Залишок - 25. Тому,$f(2)=25$.

Аналіз

Ми можемо перевірити нашу відповідь, оцінивши$f(2)$.

\[\begin{align*} f(x)&=6x^4−x^3−15x^2+2x−7 \\ f(2)&=6(2)^4−(2)^3−15(2)^2+2(2)−7 \\ &=25 \end{align*}\]

Вправа$\PageIndex{1}$

Використовуйте теорему про залишок для оцінки$f(x)=2x^5−3x^4−9x^3+8x^2+2$ в$x=−3$.

Відповідь: $f(−3)=−412$

Використання теореми фактора для розв'язання поліноміального рівняння

Теорема фактора - ще одна теорема, яка допомагає нам аналізувати поліноміальні рівняння. Це говорить нам про те, як нулі многочлена пов'язані з факторами. Нагадаємо, що алгоритм поділу.

\[f(x)=(x−k)q(x)+r\]

Якщо$k$ дорівнює нулю, то залишок$r$ дорівнює$f(k)=0$ і$f (x)=(x−k)q(x)+0$ або$f(x)=(x−k)q(x)$.

Повідомлення, написане в такому вигляді,$x−k$ є фактором$f(x)$. Можна зробити висновок, якщо$k$ дорівнює нулю$f(x)$, то$x−k$ є коефіцієнтом$f(x)$.

Аналогічно, якщо$x−k$ є коефіцієнтом$f(x)$, то залишок алгоритму поділу$f(x)=(x−k)q(x)+r$ є$0$. Це говорить нам, що$k$ це нуль.

Ця пара наслідків є теоремою фактора. Як ми скоро побачимо, многочлен ступеня$n$ в комплексній системі числення матиме$n$ нулі. Ми можемо використовувати Теорему Фактора для повного множника множника у добуток$n$ факторів. Після того, як многочлен буде повністю врахований, ми можемо легко визначити нулі многочлена.

ТЕОРЕМА ПРО ФАКТОР

Відповідно до Теореми Фактора,$k$ є нулем$f(x)$ if і тільки якщо$(x−k)$ є коефіцієнтом$f(x)$.

Як: З огляду на множник і многочлен третього ступеня, використовуйте теорему фактора для множника полінома

Використовуйте синтетичне ділення, щоб розділити многочлен на$(x−k)$.
Підтвердіть, що залишок є$0$.
Запишіть многочлен як добуток$(x−k)$ і квадратичний частка.
Якщо можливо, коефіцієнт квадратичної.
Запишіть многочлен як добуток факторів.

Приклад$\PageIndex{2}$: Using the Factor Theorem to Solve a Polynomial Equation

Показати, що$(x+2)$ є фактором$x^3−6x^2−x+30$. Знайдіть інші фактори. Використовуйте множники для визначення нулів многочлена.

Рішення

Ми можемо використовувати синтетичний поділ, щоб показати, що$(x+2)$ це множник многочлена.

\[ -2 \begin{array}{|cccc} \; 1 & −6 & −1 & 30 \\ \text{} & -2 & 16 & -30 \\ \hline \end{array} \\ \begin{array}{cccc} 1 & -8 & \; 15 & \;\;0 \end{array} \]

Залишок дорівнює нулю, тому$(x+2)$ є множником многочлена. Ми можемо використовувати алгоритм поділу, щоб записати многочлен як добуток дільника та частки:

\[(x+2)(x^2−8x+15)\]

Ми можемо перерахувати квадратичний коефіцієнт, щоб записати многочлен як

\[(x+2)(x−3)(x−5)\]

За теоремою фактора, нулі$x^3−6x^2−x+30$ є —2, 3 та 5.

Вправа$\PageIndex{2}$

Використовуйте теорему про множник, щоб знайти нулі$f(x)=x^3+4x^2−4x−16$ заданого, що$(x−2)$ є множником многочлена.

Відповідь: Нулі - 2, —2 і —4.

Використання теореми про раціональні нулі для пошуку раціональних нулів

Іншим використанням теореми про залишок є перевірка того, чи раціональне число є нулем для заданого многочлена. Але спочатку нам потрібен пул раціональних чисел для тестування. Теорема про раціональний нуль допомагає звузити кількість можливих раціональних нулів, використовуючи співвідношення множників постійного члена і факторів провідного коефіцієнта многочлена.

Розглянемо квадратичну функцію з двома нулями,$x=\frac{2}{5}$ і$x=\frac{3}{4}$. За теоремою фактора ці нулі мають множники, пов'язані з ними. Встановимо кожен множник рівним 0, а потім побудуємо вихідну квадратичну функцію без її коефіцієнта розтягування.

$альт$

Зверніть увагу, що два фактори постійного члена, 6, є двома чисельниками від початкових раціональних коренів: 2 і 3. Аналогічно два фактори від провідного коефіцієнта, 20, є двома знаменниками від початкових раціональних коренів: 5 і 4.

Можна зробити висновок, що чисельники раціональних коренів завжди будуть факторами постійного члена, а знаменники - факторами провідного коефіцієнта. Це суть теореми про раціональний нуль; це засіб, який дає нам пул можливих раціональних нулів.

ТЕОРЕМА РАЦІОНАЛЬНОГО НУЛЯ

Теорема про раціональний нуль стверджує, що якщо многочлен$f(x)=a_nx^n+a_{n−1}x^{n−1}+...+a_1x+a_0$ має цілочисельні коефіцієнти, то кожен раціональний нуль$f(x)$ має вигляд,$\frac{p}{q}$ де$p$ є коефіцієнтом постійного члена$a_0$ і$q$ є коефіцієнтом провідного коефіцієнта$a_n$.

Коли провідний коефіцієнт дорівнює 1, можливі раціональні нулі - це фактори постійного члена.

Як: Задано поліноміальну функцію$f(x)$, use the Rational Zero Theorem to find rational zeros.

Визначте всі фактори постійного терміну і всі фактори провідного коефіцієнта.
Визначте всі можливі значення$\dfrac{p}{q}$, де$p$ коефіцієнт постійного члена і$q$ є коефіцієнтом провідного коефіцієнта. Обов'язково включайте як позитивних, так і негативних кандидатів.
Визначте, які можливі нулі є фактичними нулями, оцінюючи кожен випадок$f(\frac{p}{q})$.

Приклад$\PageIndex{3}$: Listing All Possible Rational Zeros

Перерахуйте всі можливі раціональні нулі$f(x)=2x^4−5x^3+x^2−4$.

Рішення

Єдино можливими$f(x)$ раціональними нулями є частки факторів останнього члена, —4, а коефіцієнти провідного коефіцієнта, 2.

Постійний термін дорівнює —4; коефіцієнти —4 є$p=±1,±2,±4$.

Провідний коефіцієнт - 2; коефіцієнти 2 -$q=±1,±2$.

Якщо будь-який з чотирьох дійсних нулів є раціональними нулями, то вони будуть з одного з наступних факторів —4, поділених на один із факторів 2.

\[\dfrac{p}{q}=±\dfrac{1}{1},±\dfrac{1}{2} \; \; \; \; \; \; \frac{p}{q}=±\dfrac{2}{1},±\dfrac{2}{2} \; \; \; \; \; \; \dfrac{p}{q}=±\dfrac{4}{1},±\dfrac{4}{2} \nonumber\]

Зверніть увагу на те$\frac{4}{2}=2$, що$\frac{2}{2}=1$ і, які вже були перераховані. Таким чином, ми можемо скоротити наш список.

\[\dfrac{p}{q} = \dfrac{\text{Factors of the last}}{\text{Factors of the first}}=±1,±2,±4,±\dfrac{1}{2}\nonumber \]

Приклад$\PageIndex{4}$: Using the Rational Zero Theorem to Find Rational Zeros

Використовуйте теорему про раціональний нуль, щоб знайти раціональні нулі$f(x)=2x^3+x^2−4x+1$.

Рішення

Теорема про раціональний нуль говорить нам, що якщо$\frac{p}{q}$ дорівнює нулю$f(x)$, то$p$ є коефіцієнтом 1 і$q$ є коефіцієнтом 2.

\[ \begin{align*} \dfrac{p}{q}=\dfrac{factor\space of\space constant\space term}{factor\space of\space leading\space coefficient} \\[4pt] &=\dfrac{factor\space of\space 1}{factor\space of\space 2} \end{align*}\]

Коефіцієнти 1 становлять ± 1, а фактори 2 - ± 1 і ± 2. Можливі значення для$\frac{p}{q}$: ± 1 і$±\frac{1}{2}$. Це можливі раціональні нулі для функції. Ми можемо визначити, які з можливих нулів є фактичними нулями, підставивши ці значення на$x$ in$f(x)$.

\[f(−1)=2{(−1)}^3+{(−1)}^2−4(−1)+1=4\]

\[f(1)=1{(1)}^3+{(1)}^2−4(1)+1=0\]

\[f(−\dfrac{1}{2})=2{(−\dfrac{1}{2})}^3+{(−\dfrac{1}{2})}^2−4(−\dfrac{1}{2})+1=3\]

\[f(\dfrac{1}{2})=2{(\dfrac{1}{2})}^3+{(\dfrac{1}{2})}^2−4(\dfrac{1}{2})+1=−\dfrac{1}{2}\]

З них,$−1$$−\dfrac{1}{2}$, і не$\dfrac{1}{2}$ є нулями$f(x)$. 1 є єдиним раціональним нулем$f(x)$.

Вправа$\PageIndex{3}$

Використовуйте теорему про раціональний нуль, щоб знайти раціональні нулі$f(x)=x^3−5x^2+2x+1$.

Відповідь: Раціональних нулів немає.

Знаходження нулів поліноміальних функцій

Теорема про раціональний нуль допомагає нам звузити список можливих раціональних нулів для поліноміальної функції. Після того, як ми це зробили, ми можемо використовувати синтетичне ділення неодноразово, щоб визначити всі нулі поліноміальної функції.

Як: Задано поліноміальну функцію$f$, use synthetic division to find its zeros.

Використовуйте теорему про раціональний нуль, щоб перерахувати всі можливі раціональні нулі функції.
Використовуйте синтетичне ділення для оцінки заданого можливого нуля шляхом синтетичного ділення кандидата на многочлен. Якщо залишок дорівнює 0, кандидат дорівнює нулю. Якщо залишок не дорівнює нулю, відкиньте кандидата.
Повторіть крок другий, використовуючи частку, знайдену з синтетичним поділом. Якщо можливо, продовжуйте до тих пір, поки частка не стане квадратичною.
Знайти нулі квадратичної функції. Двома можливими методами розв'язання квадратики є факторинг і використання квадратичної формули.

Приклад$\PageIndex{5}$: Finding the Zeros of a Polynomial Function with Repeated Real Zeros

Знайти нулі$f(x)=4x^3−3x−1$.

Рішення

Теорема про раціональний нуль говорить нам$f(x)$, що якщо$\dfrac{p}{q}$ дорівнює нулю, то$p$ є коефіцієнтом —1 і$q$ є коефіцієнтом 4.

\[\begin{align*}\dfrac{p}{q}=\dfrac{factor\space of\space constant\space term}{factor\space of\space leading\space coefficient} \\[4pt] =\dfrac{factor\space of\space -1}{factor\space of\space 4} \end{align*}\]

Коефіцієнти —1 становлять ± 1, а коефіцієнти 4 - ± 1, ± 2 та ± 4. Можливі значення для$\dfrac{p}{q}$$±1$ are$±\dfrac{1}{2}$, і$±\dfrac{1}{4}$. Це можливі раціональні нулі для функції. Ми будемо використовувати синтетичне ділення для оцінки кожного можливого нуля, поки не знайдемо той, який дає залишок 0. Почнемо з 1.

Ділення на$(x−1)$ дає залишок 0, тому 1 є нулем функції. Многочлен може бути записаний як

\[(x−1)(4x^2+4x+1) \nonumber\]

Квадратичний - ідеальний квадрат. $f(x)$можна записати як

\[(x−1){(2x+1)}^2\nonumber\]

Ми вже знаємо, що 1 - це нуль. Інший нуль матиме кратність 2, оскільки коефіцієнт знаходиться в квадраті. Щоб знайти інший нуль, ми можемо встановити коефіцієнт, рівний 0.

\[ \begin{align*} 2x+1=0 \\[4pt] x &=−\dfrac{1}{2} \end{align*}\]

Нулі функції - 1 і$−\frac{1}{2}$ з кратністю 2.

Аналіз

Подивіться на графік функції$f$ на рис$\PageIndex{1}$. Зверніть увагу, в$x =−0.5$, графік відскакує від осі x, вказуючи парну кратність (2,4,6...) для нуля −0,5. В$x=1$, графік перетинає вісь х, вказуючи непарну кратність (1,3,5...) для нуля$x=1$.

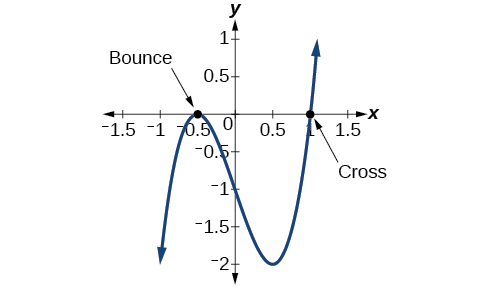
Використання фундаментальної теореми алгебри

Тепер, коли ми можемо знайти раціональні нулі для поліноміальної функції, ми розглянемо теорему, яка обговорює кількість комплексних нулів поліноміальної функції. Фундаментальна теорема алгебри говорить нам, що кожна поліноміальна функція має принаймні один комплексний нуль. Ця теорема є основою для розв'язання поліноміальних рівнянь.

Припустимо,$f$ це поліноміальна функція ступеня чотири, і$f (x)=0$. Фундаментальна теорема алгебри стверджує, що існує хоча б одне комплексне рішення, назвемо його$c_1$. За теоремою фактора ми можемо записати$f(x)$ як$x−c_1$ добуток і поліноміальний коефіцієнт. Оскільки$x−c_1$ є лінійним, частка многочлена буде третього ступеня. Тепер застосуємо фундаментальну теорему алгебри до поліноміального частки третього ступеня. У ньому буде хоча б один комплексний нуль, назвемо його$c_2$. Таким чином, ми можемо записати частку полінома як$x−c_2$ добуток і новий поліноміальний частка ступеня два. Продовжуйте застосовувати фундаментальну теорему алгебри, поки не будуть знайдені всі нулі. Їх буде чотири, і кожен з них дасть коефіцієнт$f(x)$.

ФУНДАМЕНТАЛЬНА ТЕОРЕМА АЛГЕБРИ

Фундаментальна теорема алгебри стверджує, що якщо$f(x)$ є поліномом ступеня$n > 0$, то$f(x)$ має принаймні один комплексний нуль.

Ми можемо використовувати цю теорему, щоб стверджувати,$f(x)$ що якщо поліном ступеня$n >0$, а а ненульовим дійсним числом, то$f(x)$ має точно$n$ лінійні множники

\[f(x)=a(x−c_1)(x−c_2)...(x−c_n)\]

де$c_1,c_2$,... ,$c_n$ є комплексними числами. Тому$f(x)$ має$n$ коріння, якщо ми дозволяємо множинності.

Питання і відповіді: Чи кожен многочлен має хоча б один уявний нуль?

Ні. Реальні числа - це підмножина комплексних чисел, але не навпаки. Комплексне число не обов'язково є уявним. Реальні числа також є комплексними числами.

Приклад$\PageIndex{6}$: Finding the Zeros of a Polynomial Function with Complex Zeros

Знайти нулі$f(x)=3x^3+9x^2+x+3$.

Рішення

Теорема про раціональний нуль говорить нам, що якщо$\frac{p}{q}$ дорівнює нулю$f(x)$, то$p$ є коефіцієнтом 3 і$q$ є коефіцієнтом 3.

Коефіцієнти 3 становлять ± 1 і ± 3. Можливими значеннями$\dfrac{p}{q}$, а отже, можливими раціональними нулями для функції є ±3, ±1, і$±\dfrac{1}{3}$. Ми будемо використовувати синтетичне ділення для оцінки кожного можливого нуля, поки не знайдемо той, який дає залишок 0. Почнемо з —3.

Ділення на$(x+3)$ дає залишок 0, тому —3 є нулем функції. Многочлен може бути записаний як

\[(x+3)(3x^2+1) \nonumber\]

Потім ми можемо встановити квадратичну рівну 0 і вирішити, щоб знайти інші нулі функції.

\[ \begin{align*} 3x^2+1=0 \\[4pt] x^2 &=−\dfrac{1}{3} \\[4pt] x&=±−\sqrt{\dfrac{1}{3}} \\[4pt] &=±\dfrac{i\sqrt{3}}{3} \end{align*}\]

Нулі$f(x)$ є$–3$ і$±\dfrac{i\sqrt{3}}{3}$.

Аналіз

Подивіться на графік функції$f$ на рис$\PageIndex{2}$. Зверніть увагу, що в$x =−3$, графік перетинає вісь x, вказуючи непарну кратність (1) для нуля$x=–3$. Також зверніть увагу на наявність двох поворотних точок. Це означає, що, оскільки є$3^{rd}$ градусний многочлен, ми дивимося на максимальну кількість поворотних точок. Отже, кінцева поведінка збільшення без прив'язки до правого і зменшення без прив'язки до лівого продовжиться. Таким чином, показані всі x-перехоплення для функції. Так що або кратність$x=−3$ є 1 і є два комплексних рішення, який є те, що ми знайшли, або$x =−3$ кратність в три. Так чи інакше, наш результат правильний.

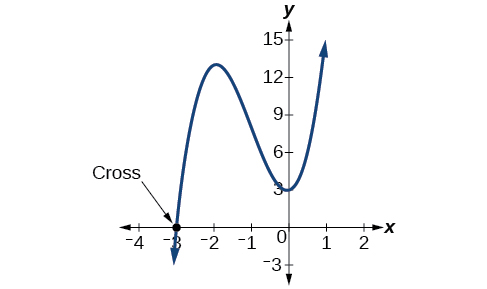
$\PageIndex{4}$

Знайти нулі$f(x)=2x^3+5x^2−11x+4$.

Рішення

Нулі є$–4$,$\frac{1}{2}$, і$1$.

Використання теореми лінійної факторизації для пошуку поліномів із заданими нулями

Життєвим наслідком фундаментальної теореми алгебри, як ми вже зазначали вище, є те, що поліноміальна функція ступеня n матиме$n$ нулі у множині комплексних чисел, якщо ми дозволимо кратності. Це означає, що ми можемо перерахувати поліноміальну функцію на$n$ фактори. Теорема про лінійну факторизацію говорить нам, що поліноміальна функція матиме таку ж кількість факторів, що і її ступінь, і що кожен множник буде у вигляді$(x−c)$, де c - комплексне число.

$f$Дозволяти поліноміальна функція з дійсними коефіцієнтами, і припустимо$a +bi$$b≠0$,, дорівнює нулю$f(x)$. Тоді, за теоремою фактора,$x−(a+bi)$ є множником$f(x)$. Для$f$ того, щоб мати реальні коефіцієнти, також$x−(a−bi)$ повинен бути коефіцієнт$f(x)$. Це вірно, тому що будь-який фактор$x−(a−bi)$, крім, при множенні на$x−(a+bi)$, залишить уявні компоненти в продукті. Тільки множення з сполученими парами усуне уявні частини і призведе до реальних коефіцієнтів. Іншими словами, якщо поліноміальна функція$f$ з дійсними коефіцієнтами має комплексний нуль$a +bi$, то комплексний сполучений також$a−bi$ повинен дорівнювати нулю$f(x)$. Це називається теоремою про складні сполучені.

ТЕОРЕМА ПРО СКЛАДНІ СПОЛУЧЕННЯ

Відповідно до Теореми про лінійну факторизацію, поліноміальна функція матиме таку ж кількість факторів, як і її ступінь, і кожен множник буде у вигляді$(x−c)$, де$c$ - комплексне число.

Якщо поліноміальна функція$f$ має дійсні коефіцієнти і комплексний нуль у вигляді$a+bi$, то комплексний спряжений нуль$a−bi$, теж дорівнює нулю.

Як

Враховуючи нулі поліноміальної функції$f$ та точку$(c, f(c))$ на графі$f$, скористайтеся теоремою лінійної факторизації, щоб знайти поліноміальну функцію.

Використовуйте нулі для побудови лінійних множників многочлена.
Помножте лінійні множники, щоб розширити многочлен.
$(c,f(c))$Підставляємо в функцію для визначення провідного коефіцієнта.
Спростити.

Приклад$\PageIndex{7}$: Using the Linear Factorization Theorem to Find a Polynomial with Given Zeros

Знайдіть поліном четвертого ступеня з дійсними коефіцієнтами, який має нулі$–3$,,,$2$$i$, такі, що$f(−2)=100$.

Рішення

Оскільки$x =i$ це нуль, за теоремою комплексного$x =–i$ спряження також дорівнює нулю. Многочлен повинен мати фактори$(x+3),(x−2),(x−i)$, і$(x+i)$. Оскільки ми шукаємо поліном 4 ступеня, і тепер маємо чотири нулі, у нас є всі чотири множники. Почнемо з множення цих факторів.

\[\begin{align} f(x) & =a(x+3)(x−2)(x−i)(x+i) \\ f(x) & =a(x^2+x−6)(x^2+1) \\ f(x) & =a(x^4+x^3−5x^2+x−6) \end{align} \]

Нам потрібно знайти,$a$ щоб забезпечити$f(–2)=100$. $f (-2)=100$Підставляємо$x=–2$ і в$f (x)$.

\[\begin{align} 100=a({(−2)}^4+{(−2)}^3−5{(−2)}^2+(−2)−6) \\ 100=a(−20) \\ −5=a \end{align} \]

Таким чином, функція полінома є

\[f(x)=−5(x^4+x^3−5x^2+x−6)\]

або

\[f(x)=−5x^4−5x^3+25x^2−5x+30\] Аналіз

Ми виявили, що обидва$i$ і$−i$ були нулями, але тільки один з цих нулів потрібно було задати. Якщо$i$ є нулем многочлена з дійсними коефіцієнтами, то також$−i$ повинен бути нулем многочлена, оскільки$−i$ є комплексним сполученим$i$.

Q&A

$2+3i$Якби були задані як нуль многочлена з дійсними коефіцієнтами,$2−3i$ також потрібно було б дорівнювати нулю?

Так. Коли будь-яке комплексне число з уявною складовою задається як нуль многочлена з дійсними коефіцієнтами, сполучений також повинен бути нулем многочлена.

$\PageIndex{5}$

Знайдіть многочлен третього ступеня з дійсними коефіцієнтами, що має нулі$5$ і$−2i$ такі, що$f (1)=10$.

Рішення

$f(x)=−\frac{1}{2}x^3+\frac{5}{2}x^2−2x+10$

Використання правила знаків Декарта

Існує простий спосіб визначити можливі числа позитивних і від'ємних дійсних нулів для будь-якої поліноміальної функції. Якщо многочлен записаний у порядку спадання, Правило знаків Декарта повідомляє нам про зв'язок між кількістю змін знаків$f(x)$ та кількістю позитивних дійсних нулів. Наприклад, функція полінома нижче має одну зміну знака.

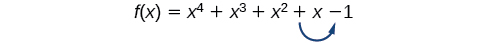
$CNX_Precalc_Figure_03_06_003.jpg$

Це говорить нам про те, що функція повинна мати 1 позитивний реальний нуль.

Існує подібна залежність між кількістю змін знаків$f(−x)$ і кількістю негативних дійсних нулів.

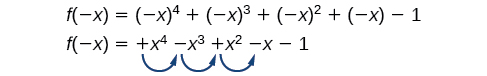
$CNX_Precalc_Figure_03_06_004.jpg$

В даному випадку$f(−x)$ має 3 знакові зміни. Це говорить нам, що$f(x)$ може мати 3 або 1 негативні реальні нулі.

ПРАВИЛО ДЕКАРТА ЗНАКІВ

Згідно з Правилом знаків Декарта, якщо ми дозволимо$f(x)=a_nx^n+a_{n−1}x^{n−1}+...+a_1x+a_0$ бути поліноміальною функцією з дійсними коефіцієнтами:

Кількість позитивних дійсних нулів або дорівнює кількості змін знаків$f(x)$ або менше кількості змін знаків на парне ціле число.
Кількість від'ємних дійсних нулів або дорівнює кількості змін знаків$f(−x)$ або менше кількості змін знаків на парне ціле число.

Приклад$\PageIndex{8}$: Using Descartes’ Rule of Signs

Скористайтеся Правилом знаків Декарта, щоб визначити можливі числа позитивних та негативних дійсних нулів для$f(x)=−x^4−3x^3+6x^2−4x−12$.

Рішення

Почніть з визначення кількості знакових змін.

Є дві зміни знаків, тому є або 2, або 0 позитивних реальних коренів. Далі оглядаємо,$f(−x)$ щоб визначити кількість негативних реальних коренів.

\[ \begin{align} f(−x) & =−{(−x)}^4−3{(−x)}^3+6{(−x)}^2−4(−x)−12 \\ f(−x) & =−x^4+3x^3+6x^2+4x−12 \end{align} \]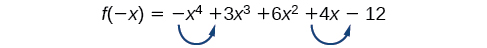

$Функція, f (-x) =-x^4+3x^3+6x^2+4x-12, має дві зміни знаків між -х ^ 4 і 3x^3, і 4x і -12. `$

Знову ж таки, є дві зміни знаків, тому є або 2, або 0 негативних реальних коренів.

Є чотири можливості, як ми бачимо в табл$\PageIndex{1}$.

Таблиця$\PageIndex{1}$
Позитивні реальні нулі	Негативні реальні нулі	Складні нулі	Всього нулів
2	2	0	4
2	0	2	4
0	2	2	4
0	0	4	4

Аналіз

Ми можемо підтвердити числа позитивних і негативних дійсних коренів, вивчивши графік функції. Див$\PageIndex{3}$. Малюнок. З графіка видно, що функція має 0 позитивних дійсних коренів і 2 негативних дійсних коренів.

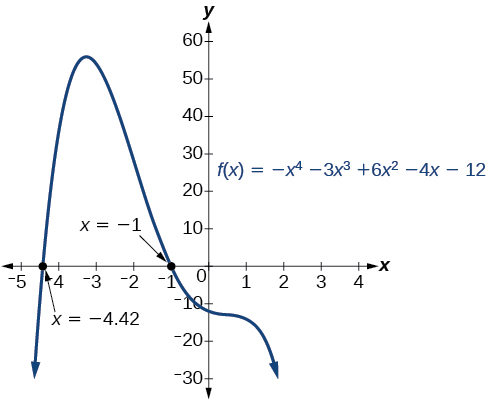
Графік f (x) =-x^4-3x^3+6x^2-4x-12 з х-перехопленнями при -4.42 та -1. — Малюнок$\PageIndex{3}$.

$\PageIndex{6}$

Скористайтеся Правилом знаків Декарта, щоб визначити максимально можливі числа позитивних та негативних дійсних нулів для$f(x)=2x^4−10x^3+11x^2−15x+12$. Використовуйте графік для перевірки чисел позитивних та від'ємних дійсних нулів для функції.

Рішення

Повинні бути 4, 2 або 0 позитивних реальних коренів і 0 негативних реальних коренів. Графік показує, що існує 2 позитивних дійсних нулів і 0 негативних дійсних нулів.

Рішення реальних додатків

Зараз ми ввели різноманітні інструменти для розв'язання поліноміальних рівнянь. Давайте використаємо ці інструменти для вирішення проблеми хлібопекарні з початку розділу.

Приклад$\PageIndex{9}$

Розв'язування поліноміальних рівнянь

Рішення

Почніть з написання рівняння для обсягу торта. Обсяг прямокутного твердого тіла задається за допомогою$V=lwh$. Нам дали, що довжина повинна бути на чотири дюйми більше ширини, так що ми можемо висловити довжину торта як$l=w+4$. Нам дали, що висота торта становить одну третину ширини, тому ми можемо висловити висоту торта як$h=\dfrac{1}{3}w$. Запишемо обсяг торта в перерахунку на ширину коржа.

\[V=(w+4)(w)(\dfrac{1}{3}w)\] \[V=\dfrac{1}{3}w^3+\dfrac{4}{3}w^2\]

Підставте заданий обсяг в це рівняння.

$351=13w^3+43w^2$Замініть 351 на V. $1053=w^3+4w^2$ помножте обидві сторони на 3. $0=w^3+7w^2−1053$Відніміть 1053 з обох сторін.

Правило знаків Декарта говорить нам, що є одне позитивне рішення. Теорема про раціональний нуль говорить нам, що можливі раціональні нулі є$\pm 1,±3,±9,±13,±27,±39,±81,±117,±351,$ і$±1053$. Ми можемо використовувати синтетичне ділення для перевірки цих можливих нулів. Тільки позитивні числа мають сенс як розміри для торта, тому нам не потрібно перевіряти будь-які негативні значення. Почнемо з тестування значень, які мають найбільший сенс як розміри для невеликого листового торта. Використовуйте синтетичне поділ для перевірки$x=1$.

$альт$

Оскільки 1 не є рішенням, ми перевіримо$x=3$.

$альт$

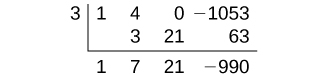
Оскільки 3 теж не є рішенням, ми будемо тестувати$x=9$.

$альт$

Синтетичне ділення дає залишок 0, тому 9 - це рішення рівняння. Ми можемо використовувати співвідношення між шириною та іншими розмірами для визначення довжини та висоти форми для торта.

$l=w+4=9+4=13$і$h=\dfrac{1}{3}w=\dfrac{1}{3}(9)=3$

Форма для торта повинна мати розміри 13 дюймів на 9 дюймів на 3 дюйми

$\PageIndex{7}$

Транспортний контейнер у формі прямокутного твердого тіла повинен мати обсяг 84 кубічних метра. Клієнт повідомляє виробнику, що через вміст довжина контейнера повинна бути на один метр більше ширини, а висота повинна бути на один метр більше, ніж в два рази більше ширини. Якими повинні бути розміри контейнера?

Рішення

3 метри на 4 метри на 7 метрів

Медіа

Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики з нулями поліноміальних функцій.

Ключові поняття

Щоб знайти$f(k)$, визначте залишок многочлена$f(x)$ при його діленні на$x−k$. Це відоме як теорема про залишок. Див$\PageIndex{1}$. Приклад.
Відповідно до Теореми Фактора,$k$ є нулем$f(x)$ if і тільки якщо$(x−k)$ є коефіцієнтом$f(x)$. Див$\PageIndex{2}$. Приклад.
Відповідно до теореми про раціональний нуль, кожен раціональний нуль поліноміальної функції з цілими коефіцієнтами дорівнюватиме множнику постійного члена, поділеному на коефіцієнт провідного коефіцієнта. Див. Приклад$\PageIndex{3}$ і Приклад$\PageIndex{4}$.
Коли провідний коефіцієнт дорівнює 1, можливі раціональні нулі - це фактори постійного члена.
Синтетичне ділення може бути використано для знаходження нулів поліноміальної функції. Див$\PageIndex{5}$. Приклад.
Відповідно до фундаментальної теореми, кожна поліноміальна функція зі ступенем більше 0 має щонайменше один комплексний нуль. Див$\PageIndex{6}$. Приклад.
Допускаючи кратність, поліноміальна функція матиме таку ж кількість факторів, як і її ступінь. Кожен коефіцієнт буде у вигляді$(x−c)$, де$c$ - комплексне число. Див$\PageIndex{7}$. Приклад.
Число додатних дійсних нулів поліноміальної функції - це або кількість знакових змін функції, або менша за кількість змін знаків на парне ціле число.
Число від'ємних дійсних нулів поліноміальної функції - це або кількість змін знаків,$f(−x)$ або менша за кількість змін знаків на парне ціле число. Див$\PageIndex{8}$. Приклад.
Поліноміальні рівняння моделюють багато реальних сценаріїв. Рішення рівнянь найпростіше зробити синтетичним діленням. Див$\PageIndex{9}$. Приклад.

Глосарій

Правило знаків Декарта

правило, яке визначає максимально можливі числа позитивних і негативних дійсних нулів на основі кількості знакових змін$f(x)$ і$f(−x)$

Теорема про коефіцієнт

$k$є нулем поліноміальної функції тоді і тільки$f(x)$ тоді, коли$(x−k)$ є множником$f(x)$

Фундаментальна теорема алгебри

поліноміальна функція зі ступенем більше 0 має щонайменше один комплексний нуль

Теорема лінійної факторизації

допускаючи кратність, поліноміальна функція матиме таку ж кількість факторів, як і її ступінь, і кожен множник буде у вигляді$(x−c)$, де$c$ - комплексне число

Теорема про раціональний нуль

можливі раціональні нулі поліноміальної функції мають вигляд,$\frac{p}{q}$ де$p$ є множником постійного члена і$q$ є коефіцієнтом провідного коефіцієнта.

Теорема про залишок

якщо многочлен$f(x)$ ділиться на$x−k$, то залишок дорівнює значенню$f(k)$