5.4: Графіки поліноміальних функцій

Last updated
Save as PDF

Page ID: 59620

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Розпізнавати характеристики графіків поліноміальних функцій.
Використовуйте факторинг, щоб знайти нулі поліноміальних функцій.
Визначте нулі і їх кратності.
Визначте поведінку кінця.
Зрозумійте взаємозв'язок між ступенем і поворотними моментами.
Функції поліномів графа.
Використовуйте теорему про проміжні значення.

Виручка в мільйоні доларів для вигаданої кабельної компанії з 2006 по 2013 рік показана в табл$\PageIndex{1}$.

Таблиця$\PageIndex{1}$
Рік	2006	2007	2008	2009	2010	2011	2012	2013
Доходи	52.4	52.8	51.2	49.5	48.6	48.6	48.7	47.1

Виручка може бути змодельована поліноміальною функцією

\[R(t)=−0.037t^4+1.414t^3−19.777t^2+118.696t−205.332\]

де$R$ представляє дохід у мільйоні доларів і$t$ представляє рік,$t=6$ що відповідає 2006. За які проміжки часу збільшується дохід компанії? За які проміжки часу знижується дохід компанії? На ці питання, поряд з багатьма іншими, можна відповісти, вивчивши графік функції полінома. Ми вже досліджували локальну поведінку квадратиків, окремий випадок поліномів. У цьому розділі ми розглянемо локальну поведінку поліномів загалом.

Розпізнавання характеристик графів поліноміальних функцій

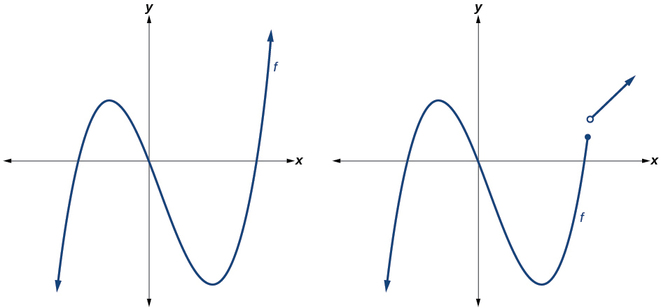
Поліноміальні функції ступеня 2 і більше мають графіки, які не мають гострих кутів; нагадаємо, що ці типи графіків називаються плавними кривими. Поліноміальні функції також відображають графіки, які не мають розривів. Криві без розривів називаються безперервними. На малюнку$\PageIndex{1}$ показаний графік, який представляє поліноміальну функцію, і графік, який представляє функцію, яка не є поліномом.

Графік f (x) = x^3-0.01x — Малюнок$\PageIndex{1}$: Графік$f(x)=x^3-0.01x$.

Приклад$\PageIndex{1}$: Recognizing Polynomial Functions

Який з графіків на малюнку$\PageIndex{2}$ представляє поліноміальну функцію?

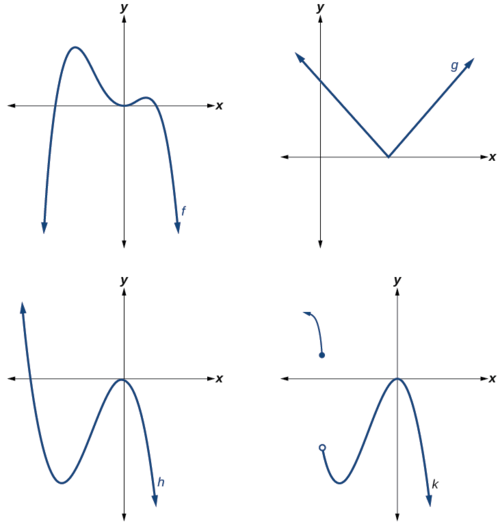
$Два графіки, в яких один має поліноміальну функцію, а інший має функцію, що нагадує многочлен, але не є. Два графіки, в яких один має поліноміальну функцію, а інший має функцію, що нагадує многочлен, але не є.$
Малюнок$\PageIndex{2}$

Рішення

Графіки$f$ і$h$ є графами поліноміальних функцій. Вони бувають гладкими і суцільними.
Графіки$g$ і$k$ є графіками функцій, які не є поліномами. Графік функції$g$ має гострий кут. Графік функції не$k$ є безперервним.

Q&A

Чи всі поліноміальні функції мають як свою область всі дійсні числа?

Так. Будь-яке дійсне число є дійсним входом для поліноміальної функції.

Використання факторингу для пошуку нулів поліноміальних функцій

Нагадаємо, що if$f$ - поліноміальна функція, значення$x$ for якої$f(x)=0$ називаються нулями$f$. Якщо рівняння поліноміальної функції може бути враховано, ми можемо встановити кожен множник рівним нулю і вирішити для нулів.

Ми можемо використовувати цей метод, щоб знайти x-перехоплення, тому що на x-перехоплення ми знаходимо вхідні значення, коли вихідне значення дорівнює нулю. Для загальних поліномів це може бути складною перспективою. Хоча квадратики можуть бути вирішені за допомогою відносно простої квадратичної формули, відповідні формули для кубічних і четвертих поліномів недостатньо прості для запам'ятовування, а формул не існує для загальних поліномів вищого ступеня. Отже, ми обмежимося трьома випадками в цьому розділі:

Багаточлен може бути врахований відомими методами: найбільший загальний фактор і триноміальний факторинг.
Многочлен задається в факторованій формі.
Для визначення перехоплень використовується технологія.

HowTo: Задано поліноміальну функцію$f$, find the x-intercepts by factoring

Набір$f(x)=0$.
Якщо поліноміальна функція не задана в факторованому вигляді:
1. Фактор будь-яких загальних мономіальних факторів.
2. Фактор будь-яких факторних біноміалів або триноміалів.
Встановіть кожен коефіцієнт рівним нулю і вирішуйте, щоб знайти x-перехоплення.

Приклад$\PageIndex{2}$: Finding the x-Intercepts of a Polynomial Function by Factoring

Знайдіть х-перехоплення$f(x)=x^6−3x^4+2x^2$.

Рішення

Ми можемо спробувати факторинг цього многочлена, щоб знайти розв'язки для$f(x)=0$.

\[\begin{align*} x^6−3x^4+2x^2&=0 & &\text{Factor out the greatest common factor.} \\ x^2(x^4−3x^2+2)&=0 & &\text{Factor the trinomial.} \\ x^2(x^2−1)(x^2−2)&=0 & &\text{Set each factor equal to zero.} \end{align*}\]

\[\begin{align*} x^2&=0 & & & (x^2−1)&=0 & & & (x^2−2)&=0 \\ x^2&=0 & &\text{ or } & x^2&=1 & &\text{ or } & x^2&=2 \\ x&=0 &&& x&={\pm}1 &&& x&={\pm}\sqrt{2} \end{align*}\].

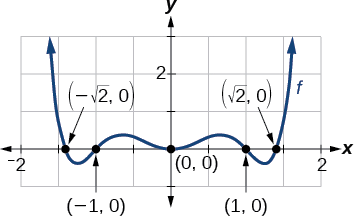
Це дає нам п'ять х-перехоплень:$(0,0)$,$(1,0)$,$(−1,0)$,$(\sqrt{2},0)$, і$(−\sqrt{2},0)$ (рис.$\PageIndex{3}$). Ми бачимо, що це рівномірна функція.

Приклад$\PageIndex{3}$: Finding the x-Intercepts of a Polynomial Function by Factoring

Знайдіть х-перехоплення$f(x)=x^3−5x^2−x+5$.

Рішення

Знайти рішення для$f(x)=0$ факторингу.

\[\begin{align*} x^3−5x^2−x+5&=0 &\text{Factor by grouping.} \\ x^2(x−5)−(x−5)&=0 &\text{Factor out the common factor.} \\ (x^2−1)(x−5)&=0 &\text{Factor the difference of squares.} \\ (x+1)(x−1)(x−5)&=0 &\text{Set each factor equal to zero.} \end{align*}\]

\[\begin{align*} x+1&=0 & &\text{or} & x−1&=0 & &\text{or} & x−5&=0 \\ x&=−1 &&& x&=1 &&& x&=5\end{align*}\]

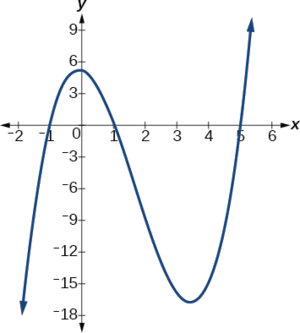
Існує три х-перехоплення:$(−1,0)$,$(1,0)$, і$(5,0)$ (рис.$\PageIndex{4}$).

Графік f (x) =x^3-5x^2-x+5 з трьома перехопленнями (-1, 0), (1, 0) та (5, 0). — Малюнок$\PageIndex{4}$: Графік$f(x)$.

Приклад$\PageIndex{4}$: Finding the y- and x-Intercepts of a Polynomial in Factored Form

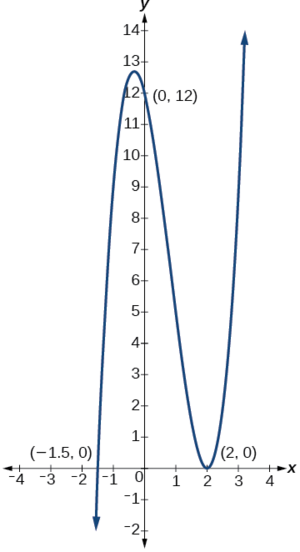
Знайдіть y- і x-перехоплення$g(x)=(x−2)^2(2x+3)$.

Рішення

Y-перехоплення можна знайти шляхом оцінки$g(0)$.

\[\begin{align*} g(0)&=(0−2)^2(2(0)+3) \\ &=12 \end{align*}\]

Таким чином, y-перехоплення є$(0,12)$.

X-перехоплення можна знайти, вирішивши$g(x)=0$.

\[(x−2)^2(2x+3)=0\]

\[\begin{align*} (x−2)^2&=0 & & & (2x+3)&=0 \\ x−2&=0 & &\text{or} & x&=−\dfrac{3}{2} \\ x&=2 \end{align*}\]

Таким чином, Х-перехоплення є$(2,0)$ і$\left(−\dfrac{3}{2},0\right)$.

Аналіз

Ми завжди можемо перевірити, чи наші відповіді є розумними, використовуючи графічний калькулятор для графічного графіка полінома, як показано на малюнку$\PageIndex{5}$.

Графік g (x) = (x-2) ^2 (2x+3) з двома його x-перехопленнями (2, 0) і (-3/2, 0) і його y-перехопленням (0, 12). — Малюнок$\PageIndex{5}$: Графік$g(x)$.

Приклад$\PageIndex{5}$: Finding the x-Intercepts of a Polynomial Function Using a Graph

Знайдіть х-перехоплення$h(x)=x^3+4x^2+x−6$.

Рішення

Цей многочлен не має факторної форми, не має загальних факторів і, здається, не може бути факторним за допомогою методів, обговорюваних раніше. На щастя, ми можемо використовувати технології для пошуку перехоплень. Майте на увазі, що деякі значення ускладнюють графіку вручну. У цих випадках ми можемо скористатися перевагами графічних утиліт.

Дивлячись на графік цієї функції, як показано на малюнку$\PageIndex{6}$, виявляється, що існують x-перехоплення на$x=−3,−2, \text{ and }1$.

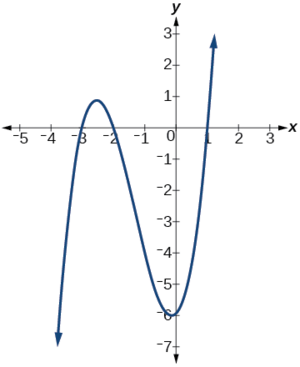
Графік h (x) =x^3+4x^2+x-6. — Малюнок$\PageIndex{6}$: Графік$h(x)$.

Ми можемо перевірити, чи є вони правильними, підставивши ці значення для$x$ і перевіривши, що
\[h(−3)=h(−2)=h(1)=0. \nonumber\]

З тих пір$h(x)=x^3+4x^2+x−6$, у нас є:

\[ \begin{align*} h(−3)&=(−3)^3+4(−3)^2+(−3)−6=−27+36−3−6=0 \\[4pt] h(−2) &=(−2)^3+4(−2)^2+(−2)−6 =−8+16−2−6=0 \\[4pt] h(1)&=(1)^3+4(1)^2+(1)−6=1+4+1−6=0 \end{align*}\]

Кожне перехоплення x відповідає нулю поліноміальної функції, а кожен нуль дає множник, тому тепер ми можемо записати многочлен у факторованій формі.

\[\begin{align*} h(x)&=x^3+4x^2+x−6 \\ &=(x+3)(x+2)(x−1) \end{align*}\]

Вправа$\PageIndex{1}$

Знайдіть y-і x-перехоплення функції$f(x)=x^4−19x^2+30x$.

Відповідь

y-перехоплення$(0,0)$;
x-перехоплює$(0,0)$$(–5,0)$,$(2,0)$,, і$(3,0)$

Визначення нулів та їх кратності

Графіки поводяться по-різному при різних х-перехопленнях. Іноді графік перетинається над горизонтальною віссю на перехопленні. Інший раз графік торкнеться горизонтальної осі і відскакує. Припустимо, наприклад, графуємо функцію

\[f(x)=(x+3)(x−2)^2(x+1)^3.\]

Зверніть увагу на малюнку$\PageIndex{7}$, що поведінка функції на кожному з x-перехоплень відрізняється.

Графік f (x) = (х+3) (x-2) ^2 (х+1) ^3. — Малюнок$\PageIndex{7}$: Виявлення поведінки графіка при х-перехопленні шляхом вивчення кратності нуля.

X-перехоплення −3 є розв'язком рівняння$(x+3)=0$. Графік проходить безпосередньо через екс-перехоплення в$x=−3$. Коефіцієнт лінійний (має ступінь 1), тому поведінка біля перехоплення подібна до поведінки лінії - вона проходить безпосередньо через перехоплення. Ми називаємо це єдиним нулем, тому що нуль відповідає одному множнику функції.

X-перехоплення 2 - повторне рішення рівняння$(x−2)^2=0$. Графік торкається осі на перехопленні і змінює напрямок. Коефіцієнт квадратичний (ступінь 2), тому поведінка біля перехоплення схожа на поведінку квадратичного - він відскакує від горизонтальної осі на перехопленні.

\[(x−2)^2=(x−2)(x−2)\]

Фактор повторюється, тобто фактор$(x−2)$ з'являється двічі. Кількість разів, коли даний коефіцієнт з'являється в факторованому вигляді рівняння многочлена, називається кратністю. Нуль, пов'язаний з цим фактором$x=2$, має кратність 2, оскільки коефіцієнт$(x−2)$ зустрічається двічі.

X-перехоплення −1 є повторним розв'язком множника$(x+1)^3=0$. Графік проходить через вісь на перехопленні, але спочатку трохи згладжується. Цей коефіцієнт є кубічним (ступінь 3), тому поведінка біля перехоплення подібна до поведінки кубічного - з тією ж S-формою біля перехоплення, що і функція інструментарію$f(x)=x^3$. Ми називаємо це потрійним нулем, або нулем з кратністю 3.

Для нулів з парними кратностями графіки торкаються або є дотичними до осі x. Для нулів з непарною кратністю графіки перетинають або перетинають вісь x. Приклади графіків поліноміальних функцій з кратністю 1, 2 та 3 див. на малюнку$\PageIndex{8}$.

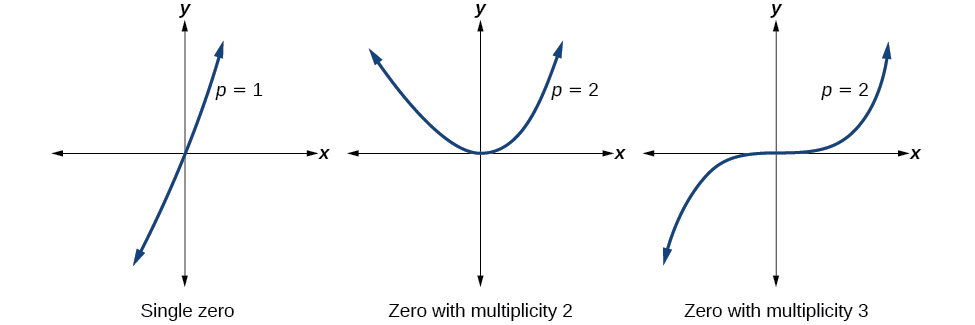
Малюнок$\PageIndex{8}$: Три графіки, що показують три різні поліноміальні функції з кратністю 1, 2 та 3.

Для більш високих рівних потужностей, таких як 4, 6 і 8, графік все одно буде торкатися і відскакувати від горизонтальної осі, але для кожного збільшення рівної потужності графік буде виглядати більш плоским, коли він наближається і залишає вісь x.

Для вищих непарних потужностей, таких як 5, 7 та 9, графік все одно перетинається через горизонтальну вісь, але для кожного збільшення непарної потужності графік буде виглядати більш плоским, коли він наближається і залишає вісь x.

Графічна поведінка многочленів при Х-перехопленнях

Якщо многочлен містить множник форми$(x−h)^p$, то поведінка біля х-перехоплення визначається степенем$p$. Ми говоримо, що$x=h$ це нуль кратності$p$.

Графік поліноміальної функції буде торкатися осі x при нулів з парними кратностями. Графік перетинає вісь x на нулі з непарною кратністю.

Сума кратностей - це ступінь поліноміальної функції.

HOWTO: Задано графік поліноміальної функції ступеня$n$, identify the zeros and their multiplicities

Якщо графік перетинає вісь x і виглядає майже лінійним на перехопленні, то це єдиний нуль.
Якщо графік торкається осі x і відскакує від осі, то це нуль з парною кратністю.
Якщо графік перетинає вісь x при нулі, то це нуль з непарною кратністю.
Сума кратностей дорівнює$n$.

Приклад$\PageIndex{6}$: Identifying Zeros and Their Multiplicities

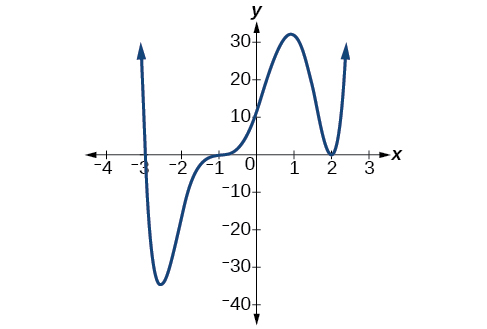
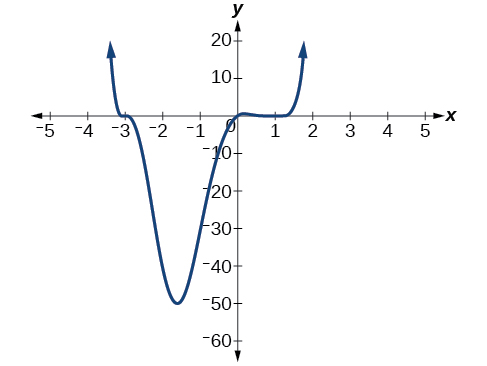
Використовуйте графік функції ступеня 6 на малюнку$\PageIndex{9}$ для ідентифікації нулів функції та їх можливих кратностей.

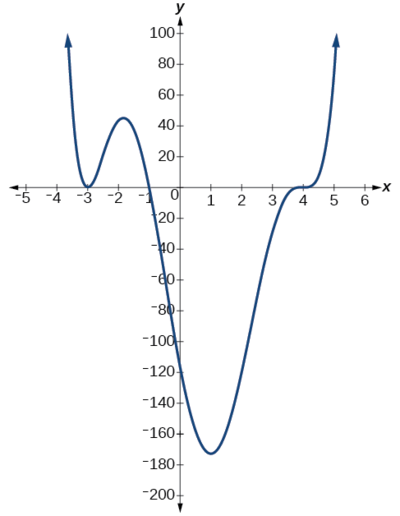
Графік парного полінома зі ступенем 6. — Малюнок$\PageIndex{9}$: Графік поліноміальної функції зі ступенем 5.

Рішення

Функція полінома має ступінь$n$. Сума кратностей повинна бути$n$.

Починаючи з лівого, перший нуль відбувається при$x=−3$. Графік стосується осі х, тому кратність нуля повинна бути парною. Нуль −3 має кратність 2.

Наступний нуль відбувається при$x=−1$. Графік виглядає майже лінійним у цій точці. Це єдиний нуль кратності 1.

Останній нуль виникає на$x=4$ .Графік перетинає вісь x, тому кратність нуля повинна бути непарною. Ми знаємо, що кратність, ймовірно, 3 і що сума кратностей, ймовірно, 6.

Вправа$\PageIndex{2}$

Використовуйте графік функції ступеня 5 на малюнку$\PageIndex{10}$ для ідентифікації нулів функції та їх кратності.

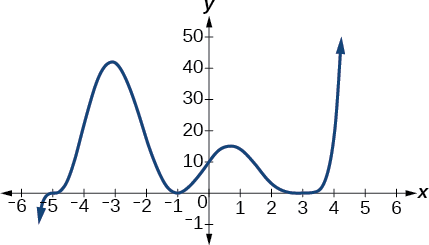
$Графік поліноміальної функції зі ступенем 5.$

Малюнок$\PageIndex{10}$: Графік поліноміальної функції зі ступенем 5.

Відповідь: Графік має нуль —5 з кратністю 1, нуль —1 з кратністю 2 і нуль 3 з парною кратністю.

Визначення кінцевої поведінки

Як ми вже дізналися, поведінка графа поліноміальної функції виду

\[f(x)=a_nx^n+a_{n−1}x^{n−1}+...+a_1x+a_0\]

буде або в кінцевому підсумку підніматися або падати, як$x$ збільшується без зв'язки і буде або підніматися, або падати, як$x$ зменшується без прив'язки. Це пов'язано з тим, що для дуже великих входів, скажімо, 100 або 1000, провідний термін домінує над розміром вихідних даних. Те ж саме стосується дуже малих входів, скажімо —100 або —1,000.

Нагадаємо, що ми називаємо цю поведінку кінцевою поведінкою функції. Як ми вказували при обговоренні квадратних рівнянь, коли провідний член поліноміальної функції$a_nx^n$, є парною степеневою функцією, оскільки$x$ збільшується або зменшується без обмежень,$f(x)$ збільшується без обмежень. Коли провідний член є непарною силовою функцією, як$x$ зменшується без зв'язки,$f(x)$ також зменшується без зв'язки; як$x$ збільшується без зв'язки,$f(x)$ також збільшується без зв'язки. Якщо провідний термін негативний, він змінить напрямок кінцевої поведінки. Малюнок$\PageIndex{11}$ підсумовує всі чотири випадки.

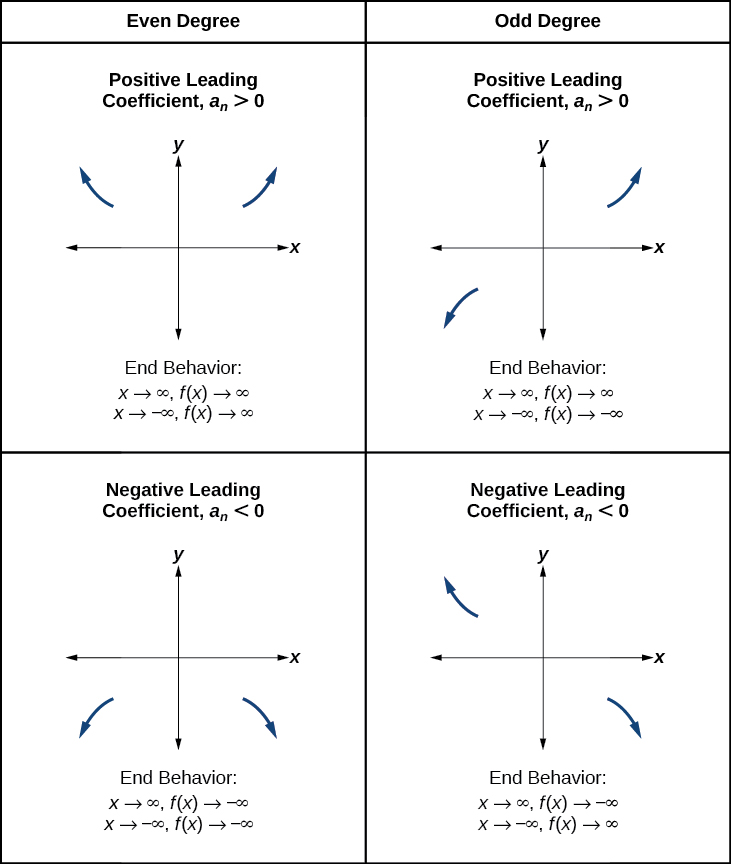
Таблиця, що показує кінцеву поведінку непарних і парних многочленів з додатними і негативними коефіцієнтами — Малюнок$\PageIndex{11}$.

Розуміння взаємозв'язку між ступенем і поворотними точками

На додаток до кінцевої поведінки, нагадаємо, що ми можемо проаналізувати локальну поведінку поліноміальної функції. Він може мати поворотний момент, коли графік змінюється від збільшення до зменшення (від зростання до падіння) або зменшення до збільшення (падіння до зростання). Подивіться на графік функції полінома на$f(x)=x^4−x^3−4x^2+4x$ малюнку$\PageIndex{12}$. Графік має три поворотні точки.

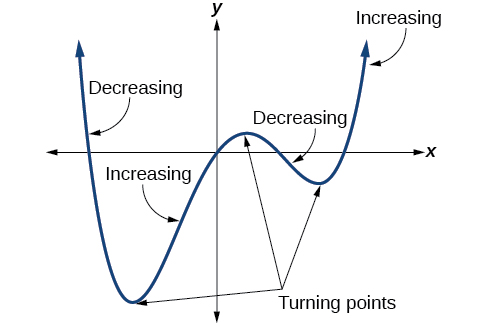
Графік f (x) =x^4-x^3-4x^2+4x, який позначає, де функція збільшується і зменшується та її поворотні точки. — Малюнок$\PageIndex{12}$: Графік$f(x)=x^4-x^3-4x^2+4x$

Ця функція$f$ є поліноміальною функцією 4-го ступеня і має 3 точки повороту. Максимальна кількість точок повороту поліноміальної функції завжди на одиницю менше ступеня функції.

Визначення: Інтерпретація поворотних точок

Поворотним моментом є точка графіка, де графік змінюється від збільшення до зменшення (від зростання до падіння) або зменшення до збільшення (падіння до зростання). Поліном ступеня$n$ буде мати в більшості$n−1$ поворотних точок.

Приклад$\PageIndex{7}$: Finding the Maximum Number of Turning Points Using the Degree of a Polynomial Function

Знайти максимальну кількість точок повороту кожної поліноміальної функції.

$f(x)=−x^3+4x^5−3x^2+1$
$f(x)=−(x−1)^2(1+2x^2)$

Рішення

а.$f(x)=−x^3+4x^5−3x^2+1$

Спочатку перепишіть поліноміальну функцію в порядку спадання:$f(x)=4x^5−x^3−3x^2+1$

Визначте ступінь поліноміальної функції. Ця поліноміальна функція має ступінь 5.

Максимальна кількість поворотних точок -$5−1=4$.

б.$f(x)=−(x−1)^2(1+2x^2)$

Спочатку визначте провідний член поліноміальної функції, якщо функція була розширена.

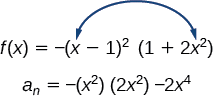
$imageedit_33_3540887475.png$

Потім визначають ступінь поліноміальної функції. Ця поліноміальна функція має ступінь 4.

Максимальна кількість поворотних точок -$4−1=3$.

Графічні поліноміальні функції

Ми можемо використовувати те, що ми дізналися про множинності, кінцеву поведінку та поворотні точки, щоб намалювати графіки поліноміальних функцій. Давайте складемо це все разом і розглянемо кроки, необхідні для графування поліноміальних функцій.

Howto: З огляду на поліноміальну функцію, намалюйте графік

Знайдіть перехоплення.
Перевірте на симетрію. Якщо функція є парною функцією, її графік симетричний щодо осі y, тобто$f(−x)=f(x)$. Якщо функція є непарною функцією, її графік симетричний щодо походження, тобто$f(−x)=−f(x)$.
Використовуйте кратності нулів, щоб визначити поведінку полінома при х-перехопленнях.
Визначте кінцеву поведінку, вивчивши провідний термін.
Використовуйте поведінку кінця та поведінку при перехопленнях для ескізу графіка.
Слідкуйте за тим, щоб число точок повороту не перевищувало на одиницю менше ступеня многочлена.
За бажанням використовуйте технологію перевірки графіка.

Приклад$\PageIndex{8}$: Sketching the Graph of a Polynomial Function

Намалюйте графік$f(x)=−2(x+3)^2(x−5)$.

Рішення

Цей графік має два x-перехоплення. При$x=−3$, коефіцієнт зводиться в квадрат, вказуючи кратність 2. Графік буде відскакувати на цьому перехопленні. В$x=5$, функція має кратність одиниці, що вказує на те, що графік буде перетинатися через вісь при цьому перехопленні.

Y-перехоплення знаходять шляхом оцінки$f(0)$.

\[\begin{align*} f(0)&=−2(0+3)^2(0−5) \\ &=−2⋅9⋅(−5) \\ &=90 \end{align*}\]

Y-перехоплення є$(0,90)$.

Крім того, ми можемо побачити провідний термін, якби цей многочлен був помножений, було б, так що кінцева поведінка полягає у вертикально відображеній кубічній$−2x3$, при цьому виходи зменшуються, коли входи наближаються до нескінченності, а виходи збільшуються, коли входи наближаються до негативної нескінченності. Див$\PageIndex{13}$. Малюнок.

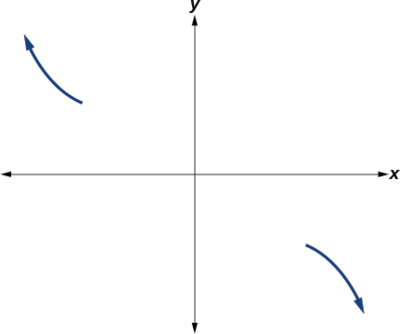
Показано розподіл за провідний термін. — Малюнок$\PageIndex{13}$: Показано розподіл за провідним терміном.

Щоб намалювати це, ми вважаємо, що:

Як$x{\rightarrow}−{\infty}$ функція$f(x){\rightarrow}{\infty}$, так ми знаємо, що графік починається в другому квадранті і зменшується до осі х.
Оскільки не$f(−x)=−2(−x+3)^2(−x–5)$ дорівнює$f(x)$, графік не відображає симетрію.
При$(−3,0)$, графік відскакує від X-осі, тому функція повинна почати збільшуватися.
В$(0,90)$, графік перетинає вісь y на перехопленні y. Див$\PageIndex{14}$. Малюнок.

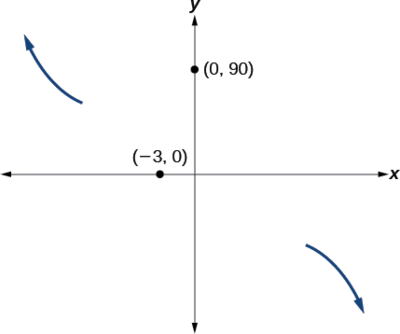
Графік поведінки кінця та перехоплення (-3, 0) та (0, 90) для функції f (x) =-2 (x+3) ^2 (x-5). — Рисунок$\PageIndex{14}$: Графік поведінки кінця і перехоплення$(0, 90)$,$(-3, 0)$ і, для функції$f(x)=-2(x+3)^2(x-5)$.

Десь після цієї точки графік повинен повернутися назад вниз або почати зменшуватися до горизонтальної осі, оскільки графік проходить через наступний перехоплення в$(5,0)$. Див$\PageIndex{15}$. Малюнок.

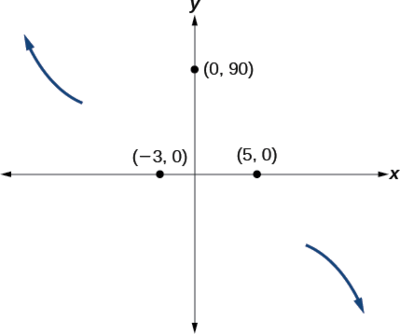
Графік поведінки кінця та перехоплення (-3, 0), (0, 90) та (5, 0) для функції f (x) =-2 (x+3) ^2 (x-5). — Рисунок$\PageIndex{15}$: Графік поведінки кінця і перехоплення$(-3, 0)$$(5, 0)$,$(0, 90)$ і, для функції$f(x)=-2(x+3)^2(x-5)$.

Як$x{\rightarrow}{\infty}$ функція$f(x){\rightarrow}−{\infty}$,

тому ми знаємо, що графік продовжує зменшуватися, і ми можемо припинити малювати графік у четвертому квадранті.

Використовуючи технологію, ми можемо створити графік для функції полінома, показаний на малюнку$\PageIndex{16}$, і переконатися, що отриманий графік виглядає як наш ескіз на малюнку$\PageIndex{15}$.

$Повний графік функції полінома f (x) =−2 (x+3) ^2 (x−5)$
Малюнок$\PageIndex{16}$: Повний графік функції полінома$f(x)=−2(x+3)^2(x−5)$.

Вправа$\PageIndex{8}$

Намалюйте графік$f(x)=\dfrac{1}{4}x(x−1)^4(x+3)^3$.

Відповідь: $альт$
Малюнок$\PageIndex{17}$: Графік$f(x)=\frac{1}{4}x(x−1)^4(x+3)^3$

Використання теореми про проміжні значення

У деяких ситуаціях ми можемо знати дві точки на графіку, але не нулі. Якщо ці дві точки знаходяться з протилежних сторін осі х, ми можемо підтвердити, що між ними є нуль. Розглянемо поліноміальну функцію, графік$f$ якої гладкий і неперервний. Теорема проміжних значень стверджує, що для двох чисел$a$ і$b$ в області$f$$f(a){\neq}f(b)$, якщо$a<b$ і, то функція$f$ приймає кожне значення між$f(a)$ і$f(b)$. Ми можемо застосувати цю теорему до окремого випадку, який корисний при графічному графіку поліноміальних функцій. Якщо точка на графіку безперервної функції$f$$x=a$ знаходиться над віссю x, а інша точка$x=b$ знаходиться нижче осі X, повинна існувати третя точка між$x=a$ і$x=b$ де графік перетинає вісь x. Називайте$(c,f(c))$ цей пункт. Це означає, що ми впевнені, що є рішення$c$ де$f(c)=0$.

Іншими словами, теорема про проміжні значення говорить нам, що коли поліноміальна функція змінюється від від'ємного значення до позитивного значення, функція повинна перетинати вісь x. $\PageIndex{18}$На малюнку видно, що між$a$ і є нуль$b$.

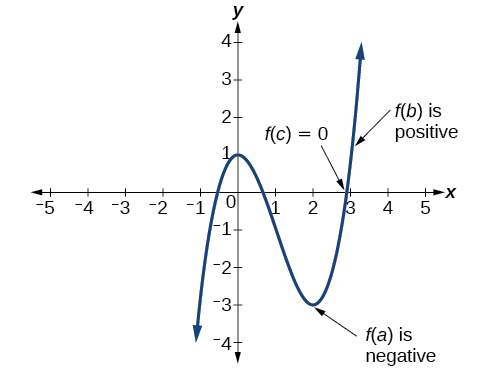
Графік непарного ступеня полінома функція, яка показує точку f (a), що негативний, f (b), що позитивний, і f (c) це 0. — Малюнок$\PageIndex{18}$: Використання теореми проміжних значень, щоб показати, що існує нуль.

Визначення: Теорема проміжних значень

$f$Дозволяти бути поліноміальною функцією. Теорема проміжних значень стверджує, що якщо$f(a)$ і$f(b)$ мають протилежні знаки, то існує принаймні одне значення$c$ між$a$ і$b$ для яких$f(c)=0$.

Приклад$\PageIndex{9}$: Using the Intermediate Value Theorem

Показати, що функція$f(x)=x^3−5x^2+3x+6$ має принаймні два дійсні нулі між$x=1$ і$x=4$.

Рішення

Для початку оцінюємо$f(x)$ за цілими значеннями$x=1,\;2,\;3,\; \text{and }4$ (Таблиця$\PageIndex{2}$).

Таблиця$\PageIndex{2}$
$x$	1	2	3	4
$f(x)$	5	0	-3	2

Ми бачимо, що один нуль відбувається при$x=2$. Крім того, оскільки$f(3)$ є негативним і$f(4)$ позитивним, за теоремою проміжного значення має бути принаймні один реальний нуль між 3 і 4.

Ми показали, що між$x=1$ і є принаймні два реальні нулі$x=4$.

Аналіз

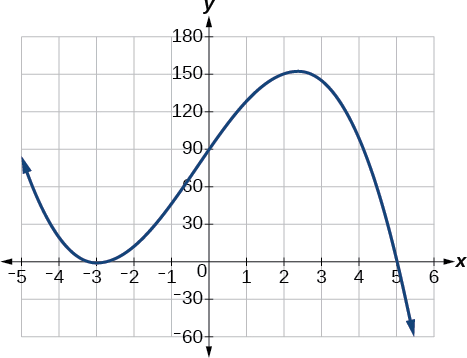
Ми також можемо побачити на графіку функції на малюнку$\PageIndex{19}$, що між$x=1$ і є два дійсні нулі$x=4$.

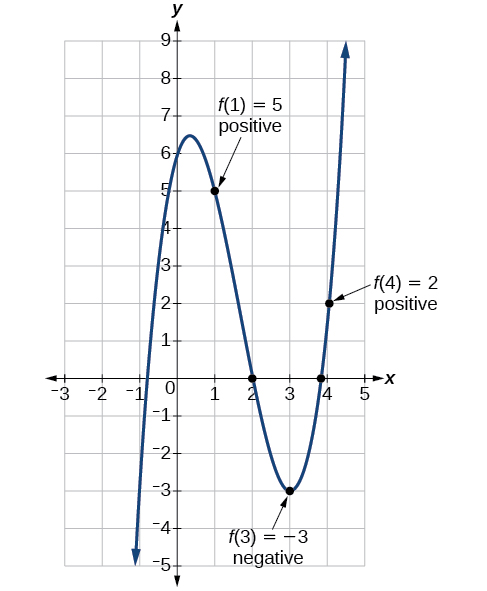
Графік f (x) =x^3-5x^2+3x+6 і показує теоремою проміжних значень, що існує два нулі, оскільки f (1) =5 і f (4) =2 є додатними, а f (3) = -3 є від'ємними. — Малюнок$\PageIndex{19}$.

Вправа$\PageIndex{4}$

Показати, що функція$f(x)=7x^5−9x^4−x^2$ має принаймні один реальний нуль між$x=1$ і$x=2$.

Відповідь: Оскільки$f$ є поліноміальною функцією, а оскільки$f(1)$ є негативним і$f(2)$ позитивним, між$x=1$ і є принаймні один реальний нуль$x=2$.

Написання формул для поліноміальних функцій

Тепер, коли ми знаємо, як знайти нулі поліноміальних функцій, ми можемо використовувати їх для написання формул на основі графіків. Оскільки поліноміальна функція, записана у факторованій формі, матиме перехоплення x, де кожен множник дорівнює нулю, ми можемо сформувати функцію, яка буде проходити через набір x-перехоплень шляхом введення відповідного набору факторів.

Примітка: Факторна форма многочленів

Якщо многочлен нижчого ступеня$p$ має горизонтальні перехоплення в$x=x_1,x_2,…,x_n$, то многочлен можна записати в факторованном вигляді:$f(x)=a(x−x_1)^{p_1}(x−x_2)^{p_2}⋯(x−x_n)^{p_n}$ де степені$p_i$ по кожному фактору можна визначити поведінкою графа при відповідному перехопленні, і коефіцієнтом розтягування$a$ може бути визначено за значенням функції, відмінної від x-перехоплення.

$альт$ Задано графік поліноміальної функції, напишіть формулу для функції.

Визначте х-перехоплення графіка, щоб знайти фактори полінома.
Вивчіть поведінку графіка при х-перехопленнях, щоб визначити кратність кожного фактора.
Знайдіть многочлен найменшого ступеня, що містить усі фактори, знайдені на попередньому кроці.
Використовуйте будь-яку іншу точку на графіку (y-перехоплення може бути найпростішим) для визначення коефіцієнта розтягування.

Приклад$\PageIndex{10}$: Writing a Formula for a Polynomial Function from the Graph

Напишіть формулу для поліноміальної функції, наведеної на малюнку$\PageIndex{20}$.

Графік додатного парного полінома з нулями при x=-3, 2, 5 та y=-2. — Малюнок$\PageIndex{20}$.

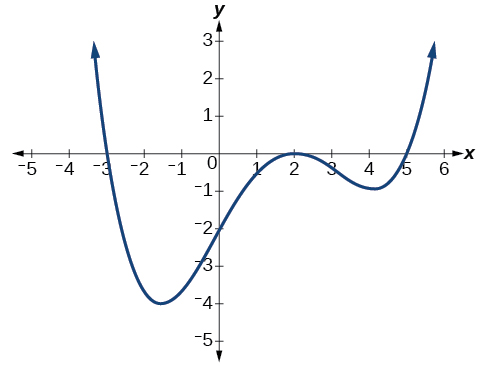
Рішення

Цей графік має три x-перехоплення:$x=−3,\;2,\text{ and }5$. Y-перехоплення розташовується за$(0,2)$ адресою .At$x=−3$ і$ x=5$, графік проходить через вісь лінійно, припускаючи, що відповідні множники многочлена будуть лінійними. При$x=2$, графік відскакує на перехопленні, припускаючи, що відповідний множник многочлена буде другого ступеня (квадратичного). Разом це дає нам

\[f(x)=a(x+3)(x−2)^2(x−5)\]

Для визначення коефіцієнта розтягування використовуємо іншу точку на графіку. Ми будемо використовувати y-перехоплення$(0,–2)$, щоб вирішити для$a$.

\[\begin{align*} f(0)&=a(0+3)(0−2)^2(0−5) \\ −2&=a(0+3)(0−2)^2(0−5) \\ −2&=−60a \\ a&=\dfrac{1}{30} \end{align*}\]

Здається, що графічний многочлен представляє функцію$f(x)=\dfrac{1}{30}(x+3)(x−2)^2(x−5)$.

Вправа$\PageIndex{5}$

З огляду на графік, показаний на малюнку$\PageIndex{21}$, напишіть формулу для показаної функції.

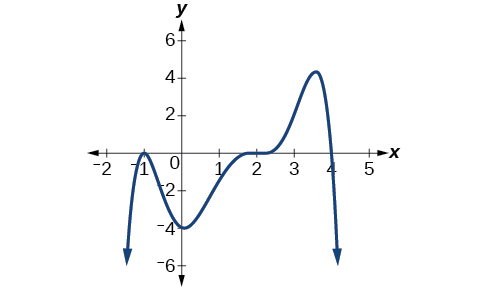
Графік від'ємного парного полінома з нулями при x=-1, 2, 4 та y=-4. — Малюнок$\PageIndex{21}$.

Відповідь: $f(x)=−\frac{1}{8}(x−2)^3(x+1)^2(x−4)$

Використання локальних і глобальних екстрем

За допомогою квадратики ми змогли алгебраїчно знайти максимальне або мінімальне значення функції, знайшовши вершину. Для загальних поліномів знаходження цих поворотних точок неможливо без більш просунутих методик з числення. Навіть тоді знайти, де відбуваються екстремуми, все ще може бути алгебраїчно складним завданням. Поки ми будемо оцінювати місця поворотних точок, використовуючи технологію для створення графіка.

Кожен поворотний момент являє собою локальний мінімум або максимум. Іноді точкою повороту є найвища або найнижча точка на всьому графіку. У цих випадках ми говоримо, що переломним моментом є глобальний максимум або глобальний мінімум. Вони також називаються абсолютними максимальними і абсолютними мінімальними значеннями функції.

Примітка: Локальні та глобальні екстреми

Локальний максимум або локальний мінімум в$x=a$ (іноді називається відносним максимумом або мінімумом відповідно) - це вихід у найвищій або найнижчій точці на графіку у відкритому інтервалі навколо$x=a$ .Якщо функція має локальний максимум at$a$, то$f(a){\geq}f(x)$ для всіх $x$у відкритому проміжку навколо$x=a$. Якщо функція має локальний мінімум at$a$, то$f(a){\leq}f(x)$ для всіх$x$ у відкритому інтервалі навколо$x=a$.

Глобальний максимум або глобальний мінімум - це вихід у найвищій або найнижчій точці функції. Якщо функція має глобальний максимум at$a$, то$f(a){\geq}f(x)$ для всіх$x$. Якщо функція має глобальний мінімум at$a$, то$f(a){\leq}f(x)$ для всіх$x$.

Ми можемо побачити різницю між локальними та глобальними екстремами на малюнку$\PageIndex{22}$.

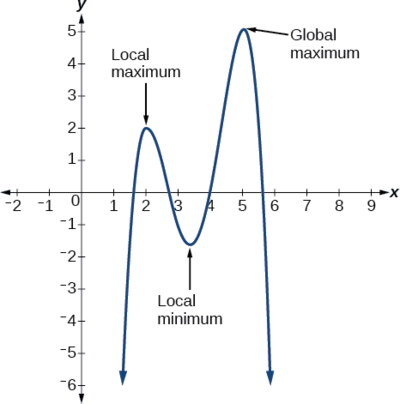
Рисунок$\PageIndex{22}$: Графік парного полінома, який позначає локальний максимум і мінімум і глобальний максимум.

$альт$ Чи всі поліноміальні функції мають глобальний мінімум або максимум?

Ні. Тільки поліноміальні функції парного ступеня мають глобальний мінімум або максимум. Наприклад, не$f(x)=x$ має ні глобального максимуму, ні глобального мінімуму.

Приклад$\PageIndex{11}$: Using Local Extrema to Solve Applications

Коробка з відкритим верхом повинна бути побудована шляхом вирізання квадратів з кожного кута 14 см на 20 см листа пластику, а потім склавши вгору по сторонам. Знайдіть розмір квадратів, які слід вирізати, щоб максимально збільшити обсяг, укладений коробкою.

Рішення

Ми почнемо цю проблему з малювання такої картинки на малюнку$\PageIndex{23}$, що позначає ширину вирізаних квадратів змінною,$w$.

Малюнок$\PageIndex{23}$: Схема прямокутника з чотирма квадратами по кутах.

Зверніть увагу, що після того, як з кожного кінця вирізається квадрат, він залишає прямокутник$a(14−2w)$$(20−2w)$ см на см для основи ящика, а коробка буде висотою$w$ см. Це надає обсяг

\[\begin{align*} V(w)&=(20−2w)(14−2w)w \\ &=280w−68w^2+4w^3 \end{align*}\]

Зверніть увагу, оскільки множники є$20–2w$$14–2w$, і$w$, три нулі є$10, \,7,$ і$0,) respectively. Because a height of \(0$ см не є розумним, ми вважаємо тільки нулі$10$ і$7.$ Найкоротша сторона,$14$ і ми відрізаємо два квадрати, так що значення$w$ можуть приймати на є більше нуля або менше, ніж$7.$ Це означає, що ми обмежимо область цієї функції до$0<w<7$ .Використовуючи технологію для ескізу графіка$V(w)$ на цій розумній області, ми отримуємо такий графік на малюнку$\PageIndex{24}$. Ми можемо використовувати цей графік, щоб оцінити максимальне значення для обсягу, обмежене значеннями,$w$ які є розумними для цієї задачі - значеннями від 0 до 7.

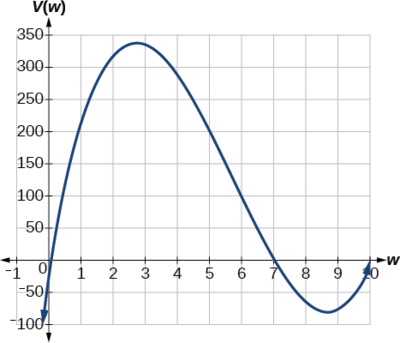
Графік V (w) = (20-2w) (14-2w) w, де вісь x позначена w, а вісь y позначена V (w). — Малюнок$\PageIndex{24}$: Графік$V(w)=(20-2w)(14-2w)w$

З цього графіка ми звернемо увагу лише на частину розумного домену,$[0, 7]$. Ми можемо оцінити максимальне значення приблизно 340 кубічних см, що відбувається, коли квадрати становлять близько 2,75 см з кожного боку. Щоб покращити цю оцінку, ми могли б використовувати розширені функції нашої технології, якщо вони доступні, або просто змінити наше вікно, щоб збільшити масштаб на нашому графіку, щоб створити малюнок$\PageIndex{25}$.

Графік V (w) = (20-2w) (14-2w) w, де вісь x позначена w, а вісь y позначена V (w) на області [2.4, 3]. — Малюнок$\PageIndex{25}$: Графік$V(w)=(20-2w)(14-2w)w$.

З цієї збільшеної точки зору ми можемо уточнити нашу оцінку для максимального обсягу приблизно до 339 кубічних см, коли квадрати вимірюють приблизно 2,7 см з кожного боку.

Вправа$\PageIndex{1}$

Використовуйте технологію, щоб знайти максимальне і мінімальне значення на інтервалі$[−1,4]$ функції$f(x)=−0.2(x−2)^3(x+1)^2(x−4)$.

Відповідь: Мінімум відбувається приблизно в точці$(0,−6.5)$,
а максимум припадає приблизно в точці$(3.5,7)$.

Ключові поняття

Поліноміальні функції ступеня 2 і більше - це гладкі, безперервні функції.
Щоб знайти нулі поліноміальної функції, якщо вона може бути врахована, множник функції і встановіть кожен множник рівним нулю.
Інший спосіб знайти x-перехоплення поліноміальної функції - це графік функції та визначення точок, в яких графік перетинає вісь x.
Кратність нуля визначає, як графік поводиться при х-перехопленнях.
Графік многочлена буде перетинати горизонтальну вісь на нуль з непарною кратністю.
Графік многочлена буде стосуватися горизонтальної осі при нулі з парною кратністю.
Кінцева поведінка поліноміальної функції залежить від провідного члена.
Графік поліноміальної функції змінює напрямок у своїх поворотних точках.
Поліноміальна функція ступеня$n$ має в більшості$n−1$ поворотних точок.
Для побудови графіків поліноміальних функцій знайдіть нулі та їх кратності, визначте кінцеву поведінку та переконайтеся, що кінцевий графік має найбільше$n−1$ поворотних точок.
Графік поліноміальної функції допомагає оцінити локальні та глобальні екстремуми.
Теорема про проміжні значення говорить нам, що якщо$f(a)$ і$f(b)$ мають протилежні знаки, то існує принаймні одне значення$c$ між$a$ і$b$ для яких$f(c)=0$.

Глосарій

глобальна максимальна
найвища точка повороту на графіку;$f(a)$ де$f(a){\geq}f(x)$ для всіх$x$.

глобальна мінімальна
найнижча точка повороту на графіку;$f(a)$ де$f(a){\leq}f(x)$ для всіх$x$.

Теорема проміжних значень
для двох чисел$a$ і$b$ в області$f$, якщо$a<b$ і$f(a){\neq}f(b)$, то функціяf приймає кожне значення між$f(a)$ і$f(b)$; конкретно, коли поліноміальна функція змінюється з від'ємного значення на a додатне значення, функція повинна перетинати вісь x

кратність кількість разів заданий коефіцієнт з'являється у факторованій формі рівняння полінома; якщо многочлен містить множник виду$(x−h)^p$,$x=h$ дорівнює нулю кратності$p$.

Таблиця\(\PageIndex{2}\)
\(x\)	1	2	3	4
\(f(x)\)	5	0	-3	2