Skip to main content
LibreTexts - Ukrayinska

1.3: Основна факторизація

  1. Last updated
  2. Save as PDF
  • Page ID
    58542

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Огляд

    • Прості та складені числа
    • Основний принцип арифметики
    • Просте факторизація цілого числа

    Прості та складені числа

    Зверніть увагу, що єдиними факторами 7 є 1 і 7 самі, і що єдиними факторами 23 є 1 і 23 самі.

    Визначення: Просте число

    Ціле число більше 1, чиї тільки цілі числові множники є самим собою, а 1 називається простим числом.

    Перші сім простих чисел -

    2, 3, 5, 7, 11, 13 і 17

    Число 1 не вважається простим числом, а число 2 є першим і єдиним парним числом.
    Багато чисел мають інші фактори, ніж вони самі і 1. Наприклад, множниками 28 є 1, 2, 4, 7, 14 і 28 (так як кожне з цих цілих чисел і тільки ці цілі числа ділиться на 28 без залишку).

    Визначення: Складене число

    Ціле число, яке складається з факторів, відмінних від себе і 1, називається складеним числом. Складені числа не є простими числами.


    Деякі складові числа - 4, 6, 8, 10, 12 і 15.

    Основний принцип арифметики

    Прості числа дуже важливі при вивченні математики. Їх ми скоро будемо використовувати в нашому дослідженні дробів. Ми зараз, однак, познайомимося з важливим математичним принципом.

    Визначення: Фундаментальний принцип арифметики

    За винятком порядку множників, кожне ціле число, крім 1, може бути враховано одним і лише одним способом як добуток простих чисел.

    Визначення: Просте факторизація

    Коли число враховується так, що всі його фактори є простими числами, факторизація називається простим факторизацією числа.

    Набір зразків A

    Приклад\(\PageIndex{1}\)

    Знайдіть просте множник 10.

    \(10=2 · 5\)

    І 2, і 5 є простими числами. Таким чином, 2 · 5 - це просте факторизація 10.

    Приклад\(\PageIndex{2}\)

    Знайдіть просте факторизацію 60.

    60 = 2 · 30 30 не є простим. 30 = 2 · 15

    = 2 · 2 · 15 15 не є простим. 15 = 3 · 5

    = 2 · 2 · 3 · 5 Ми будемо використовувати експоненти. 2 · 2 =\(2^2\)

    =\(2^2\) · 3 · 5


    Числа 2, 3 і 5 є простими числами. Таким чином, 2 2 · 3 · 5 - це просте факторизація 60.

    Приклад\(\PageIndex{3}\)

    Знайдіть просте факторизацію 11.

    11 - це просте число. Просте факторизація застосовується лише до складених чисел.

    Просте факторизація цілого числа

    Наступний метод забезпечує спосіб знаходження простого факторизації цілого числа. Наступні приклади використовуватимуть метод і зроблять його більш зрозумілим.

    1. Розділіть число багаторазово на найменше просте число, яке буде ділитися на число без залишку.
    2. Коли просте число, яке використовується на кроці 1, більше не ділиться на задане число без залишку, повторіть процес з наступним найбільшим простим числом.
    3. Продовжуйте цей процес, поки частка не буде дорівнює 1.
    4. Проста факторизація заданого числа є добутком всіх цих простих дільників.

    Набір зразків B

    Приклад\(\PageIndex{4}\)

    Знайдіть просте факторизацію 60.

    Так як 60 - парне число, воно ділиться на 2. Ми будемо неодноразово ділити на 2, поки більше не зможемо (коли почнемо отримувати залишок). Розділимо наступним чином.

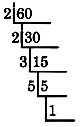
    Першочергова факторизація шістдесят. Дивіться longdesc для повного опису.

    30 знову ділиться на 2.

    15 не ділиться на 2, а ділиться на 3, наступне за величиною просте.

    5 не ділиться на 3, а ділиться на 5, наступне за величиною просте.

    Частка дорівнює 1, тому ми зупиняємо процес

    ділення Просте факторизація 60 є добутком всіх цих дільників.

    60 = 2 · 2 · 3 · 5 Ми будемо використовувати експоненти, коли це можливо

    60 =\(2^2\) · 3 · 5

    Приклад\(\PageIndex{5}\)

    Знайдіть просте факторизацію 441.

    Оскільки 441 - непарне число, воно не ділиться на 2. Ми спробуємо 3, наступний за величиною прайм.

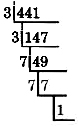
    Першочергова факторизація чотириста сорок одна. Дивіться longdesc для повного опису.

    147 ділиться на 3.

    49 ділиться не на 3 ні на 5, а на 7.

    7 ділиться на 7.

    Частка дорівнює 1, тому ми зупиняємо процес поділу.

    Просте факторизація 441 є добутком всіх дільників.

    441 = 3 · 3 · 7 · 7 Ми будемо використовувати експоненти, коли це можливо.

    441 =\(3^2\) · \(7^2\)

    Вправи

    Для наступних задач визначте, які цілі числа є простими, а які складовими.

    Вправа\(\PageIndex{1}\)

    23

    Відповідь

    прем'єр

    Вправа\(\PageIndex{2}\)

    25

    Відповідь

    композитних

    Вправа\(\PageIndex{3}\)

    27

    Відповідь

    композитних

    Вправа\(\PageIndex{4}\)

    2

    Відповідь

    прем'єр

    Вправа\(\PageIndex{5}\)

    3

    Відповідь

    прем'єр

    Вправа\(\PageIndex{6}\)

    5

    Відповідь

    прем'єр

    Вправа\(\PageIndex{7}\)

    7

    Відповідь

    прем'єр

    Вправа\(\PageIndex{8}\)

    9

    Відповідь

    композитних

    Вправа\(\PageIndex{9}\)

    11

    Відповідь

    прем'єр

    Вправа\(\PageIndex{10}\)

    34

    Відповідь

    композитних

    Вправа\(\PageIndex{11}\)

    55

    Відповідь

    композитних

    Вправа\(\PageIndex{12}\)

    63

    Відповідь

    композитних

    Вправа\(\PageIndex{13}\)

    1044

    Відповідь

    композитних

    Вправа\(\PageIndex{14}\)

    339

    Відповідь

    композитних

    Вправа\(\PageIndex{15}\)

    209

    Відповідь

    композитних

    Для наступних задач знайдіть просте факторизацію кожного цілого числа. Використовуйте показники на повторюваних факторах.

    Вправа\(\PageIndex{16}\)

    26

    Вправа\(\PageIndex{17}\)

    38

    Відповідь

    2 · 19

    Вправа\(\PageIndex{18}\)

    54

    Вправа\(\PageIndex{19}\)

    62

    Відповідь

    2 · 31

    Вправа\(\PageIndex{20}\)

    56

    Вправа\(\PageIndex{21}\)

    176

    Відповідь

    \(2^4\)·\(11\)

    Вправа\(\PageIndex{22}\)

    480

    Вправа\(\PageIndex{23}\)

    819

    Відповідь

    \(3^2\)·\(7\) · \(13\)

    Вправа\(\PageIndex{24}\)

    2025

    Вправа\(\PageIndex{25}\)

    148 225

    Відповідь

    \(5^2\)·\(7^2\) · \(11^2\)