19.5: Вправи

Last updated
Save as PDF

Page ID: 64370

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

1

Намалюйте схему решітки для набору потужності$X = \{ a, b, c, d \}$ з встановленим співвідношенням включення,$\subset\text{.}$

2

Намалюйте діаграму для множини натуральних чисел, які є дільниками чи$30\text{.}$ є ця позиція булевою алгеброю?

3

Намалюйте схему решітки підгруп${\mathbb Z}_{12}\text{.}$

4

$B$Дозволяти бути безліч натуральних чисел, які є дільниками$210\text{.}$ Визначити порядок на$B$,$a \preceq b$ якщо$a \mid b\text{.}$ Доведіть, що$B$ це логічна алгебра. Знайдіть набір$X$ такий, який$B$ є ізоморфним до${\mathcal P}(X)\text{.}$

5

Довести або спростувати:${\mathbb Z}$ є poset під відношення,$a \preceq b$ якщо$a \mid b\text{.}$

6

Намалюйте схему перемикання для кожного з наступних логічних виразів.

$\displaystyle (a \vee b \vee a') \wedge a$
$\displaystyle (a \vee b)' \wedge (a \vee b)$
$\displaystyle a \vee (a \wedge b)$
$\displaystyle (c \vee a \vee b) \wedge c' \wedge (a \vee b)'$

7

Намалюйте схему, яка буде замкнута рівно тоді, коли тільки один з трьох вимикачів$a\text{,}$$b\text{,}$ і$c$ замикається.

8

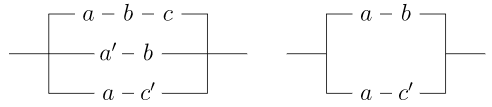
Довести або спростувати, що дві схеми показані еквівалентні.

$clipboard_e5662dbc2f7ce018ed67a8d7fd8774ac7.png$

9

$X$Дозволяти бути скінченним множиною, що містить$n$ елементи. Доведіть, що$|{\cal P}(X)| = 2^n\text{.}$ зробити висновок, що порядок будь-якої скінченної булевої алгебри повинен бути$2^n$ для деяких$n \in {\mathbb N}\text{.}$

10

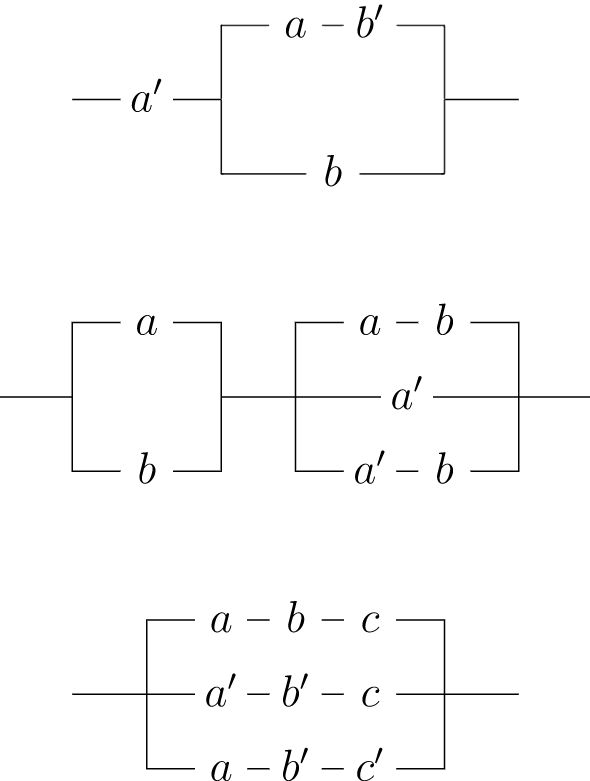
Для кожної з наведених схем напишіть логічне вираз. Якщо схема може бути замінена на одну з меншою кількістю перемикачів, дайте логічне вираз і намалюйте схему для нової схеми.

$clipboard_e71296a28342c24abfd0d3d8babc75aa2.png$

11

Довести або спростувати: множина всіх ненульових цілих чисел є решіткою, де$a \preceq b$ визначається$a \mid b\text{.}$

12

$L$Дозволяти бути непорожнім множиною з двома бінарними операціями$\vee$ і$\wedge$ задовольняє комутативний, асоціативний, ідемпотентний і поглинання законів. Ми можемо визначити частковий порядок на$L\text{,}$ як в теоремі$19.14$,$a \preceq b$ якщо$a \vee b = b\text{.}$ Довести, що найбільша нижня$a$ межа і$b$ є$a \wedge b\text{.}$

13

$G$Дозволяти бути групою і$X$ бути множиною підгруп$G$ упорядкованих множинно-теоретичного включення. Якщо$H$ і$K$ є підгрупами$G\text{,}$ показати, що найменша верхня$H$ межа і$K$ є підгрупою, що генерується$H \cup K\text{.}$

14

Дозвольте$R$ бути кільцем і припустимо, що$X$ це сукупність ідеалів$R\text{.}$ Шоу,$X$ тобто поза, упорядкована множинно-теоретичним включенням,$\subset\text{.}$ Визначте зустріч двох ідеалів$I$$I \cap J$ і$J$ в$X$ і об'єднання$I$ і$J$ шляхом $I + J\text{.}$Доведіть, що сукупність ідеалів$R$ є решіткою під цими операціями.

15

$B$Дозволяти булева алгебра. Доведіть кожну з наступних ідентичностей.

$a \vee I = I$і$a \wedge O = O$ для всіх$a \in B\text{.}$
Якщо$a \vee b = I$ і$a \wedge b = O\text{,}$ тоді$b = a'\text{.}$
$(a')'=a$для всіх$a \in B\text{.}$
$I' = O$і$O' = I\text{.}$
$(a \vee b)' = a' \wedge b'$і$(a \wedge b)' = a' \vee b'$ (закони Де Моргана).

16

Намалювавши відповідні діаграми, завершіть доказ теореми,$19.30$ щоб показати, що функції перемикання утворюють булеву алгебру.

17

$B$Дозволяти булева алгебра. Визначте бінарні операції$+$ і$\cdot$$B$ на

\ begin {align*} a + b & = (a\ клин b')\ vee (a'\ клин b)\\ a\ cdot b & = a\ клин b\ текст {.} \ end {вирівнювати*}

Доведіть, що$B$ це комутативне кільце при цих операціях задовольняє$a^2 = a$ для всіх$a \in B\text{.}$

18

$X$Дозволяти бути poset таким, що для кожного$a$ і$b$ в$X\text{,}$ будь-якому$a \preceq b$ або$b \preceq a\text{.}$ Тоді кажуть, що$X$ це повністю впорядкований набір.

Є$a \mid b$ загальним замовленням на${\mathbb N}\text{?}$
Доведіть, що${\mathbb N}\text{,}$${\mathbb Z}\text{,}$${\mathbb Q}\text{,}$ і${\mathbb R}$ повністю впорядковані набори за звичайним замовленням$\leq\text{.}$

19

Нехай$X$ і$Y$ бути посетами. Карта зберігає$\phi : X \rightarrow Y$ порядок, якщо$a \preceq b$ означає, що$\phi(a) \preceq \phi(b)\text{.}$ Let$L$ and$M$ be решітки. Карта$\psi: L \rightarrow M$ - це гратчастий гомоморфізм, якщо$\psi( a \vee b ) = \psi(a) \vee \psi(b)$ і$\psi( a \wedge b ) = \psi(a) \wedge \psi(b)\text{.}$ Показати, що кожен гомоморфізм решітки зберігає порядок, але це не так, що кожен гомоморфізм, що зберігає порядок, є гратчастим гомоморфізмом.

20

$B$Дозволяти булева алгебра. Доведіть, що$a = b$ якщо і тільки якщо$(a \wedge b') \vee ( a' \wedge b) = O$ для$a, b \in B\text{.}$

21

$B$Дозволяти булева алгебра. Доведіть, що$a = O$ якщо і тільки якщо$(a \wedge b') \vee ( a' \wedge b) = b$ для всіх$b \in B\text{.}$

22

$L$$M$Дозволяти і бути решітки. Визначте відношення порядку за$L \times M$ допомогою$( a, b) \preceq (c, d)$ if$a \preceq c$ і$b \preceq d\text{.}$ Показати, що$L \times M$ це решітка в цьому частковому порядку.