19.3: Алгебра електричних кіл

Last updated
Save as PDF

Page ID: 64363

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Корисність булевих алгебр стає все більш очевидною протягом останніх кількох десятиліть з розвитком сучасного комп'ютера. Схемотехніка комп'ютерних мікросхем може бути виражена термінами булевих алгебр. У цьому розділі ми розробимо булеву алгебру електричних схем та вимикачів; однак ці результати можна легко узагальнити до проектування інтегральної комп'ютерної схеми.

Вимикач - це пристрій, розташований в якійсь точці електричного кола, що управляє протіканням струму по ланцюгу. Кожен вимикач має два можливих стану: він може бути розімкнутим, і не допускати проходження струму по ланцюгу, або ж він може бути замкнутий, і допускати проходження струму. Ці держави є взаємовиключними. Ми вимагаємо, щоб кожен перемикач знаходився в тому чи іншому стані - вимикач не може бути відкритий і закритий одночасно. Крім того, якщо один вимикач завжди знаходиться в тому ж стані, що і інший, ми позначимо обидва однією буквою; тобто два перемикача, які обидва позначені однією буквою, завжди$a$ будуть відкриті одночасно і закриті одночасно.

З огляду на два перемикача, ми можемо побудувати два основних типи схем. Два вимикача$a$ і$b$ знаходяться послідовно, якщо вони складають схему типу, яка проілюстрована на малюнку$19.25$. Струм може проходити між клемами$A$ і$B$ в послідовному ланцюзі тільки в тому випадку, якщо обидва вимикача$a$ і$b$ замкнуті. Ми позначимо цю комбінацію вимикачів$a \wedge b\text{.}$ двома вимикачами$a$ і$b$ знаходяться паралельно, якщо вони утворюють схему типу, яка фігурує на малюнку$19.26$. У разі паралельної ланцюга струм може проходити між$A$ і в тому випадку,$B$ якщо будь-який з вимикачів замкнутий. Позначимо паралельне поєднання ланцюгів$a$ і$b$ по$a \vee b\text{.}$

$clipboard_ee55a276b702a98ed11ce74a6a9ec4214.png$

$Figure \text { } 19.25.$$a \wedge b$

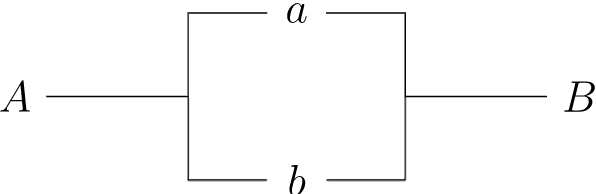
$clipboard_e14a7991a53145add6a510c6b72201807.png$

$Figure \text { } 19.26.$$a \vee b$

Ми можемо побудувати більш складні електричні схеми з послідовних та паралельних ланцюгів, замінивши будь-який вимикач у ланцюзі одним із цих двох основних типів схем. Схеми, побудовані таким чином, називаються послідовно-паралельними схемами.

Ми розглянемо дві схеми еквівалентними, якщо вони діють однаково. Тобто, якщо встановити вимикачі в еквівалентних схемах точно так само, ми отримаємо той же результат. Наприклад, в послідовному ланцюзі точно$a \wedge b$ так само, як$b \wedge a\text{.}$ Зверніть увагу, що це саме комутативний закон для булевих алгебр. Насправді множина всіх послідовно-паралельних схем утворює булеву алгебру під операціями$\vee$ і$\wedge\text{.}$ Ми можемо використовувати діаграми для перевірки різних аксіом булевої алгебри. Розподільний закон,$a \wedge ( b \vee c ) = (a \wedge b ) \vee ( a \wedge c )\text{,}$ проілюстрований на рис$19.27$. Якщо$a$ це вимикач, то$a'$ це вимикач, який завжди відкритий, коли$a$ закритий і завжди закритий, коли$a$ відкритий. Ланцюг, який завжди замкнутий, знаходиться$I$ в нашій алгебрі; ланцюг, який завжди відкритий є$O\text{.}$ Закони для$a \wedge a' = O$ і$a \vee a' = I$ показані в$Figure 19.28$.

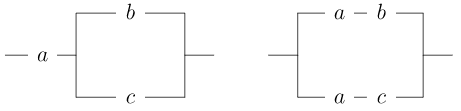
$clipboard_e6e2296c11fcd655712024cbcd49ffc0d.png$

$Figure \text { } 19.27.$$a \wedge ( b \vee c ) = (a \wedge b ) \vee ( a \wedge c )$

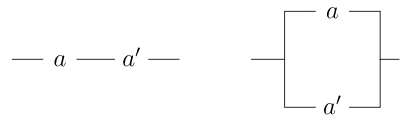
$clipboard_e4168dd26e32fbe6020dd1fb7ed27b4e9.png$

$Figure \text { } 19.28.$$a \wedge a' = O$і$a \vee a' = I$

Приклад$19.29$

Кожен логічний вираз являє собою схему перемикання. Наприклад, з огляду на вираз$(a \vee b) \wedge (a \vee b') \wedge (a \vee b)\text{,}$

Рішення

ми можемо побудувати схему на малюнку$19.32$.

Теорема$19.30$

Безліч всіх схем є булевою алгеброю

Ми залишаємо як вправу доказ цієї теореми для аксіом булевої алгебри ще не перевірений. Тепер ми можемо застосувати методи булевих алгебр до теорії перемикання.

Приклад$19.31$

З огляду на складну схему, тепер ми можемо застосувати методи булевої алгебри, щоб звести її до більш простого. Розглянемо схему на рис$19.32$. Так як

\ begin {align*} (a\ vee b)\ клин (a\ vee b')\ клин (a\ vee b) & = (a\ vee b)\ клин (a\ vee b)\ клин (a\ vee b)\\ vee b)\\ vee b)\\ vee b ')\\ & = a\ vee O\\ & = a\ текст {,}\ end {вирівнювати*}

Рішення

ми можемо замінити більш складну схему схемою, що містить один вимикач$a$ і досягти тієї ж функції.

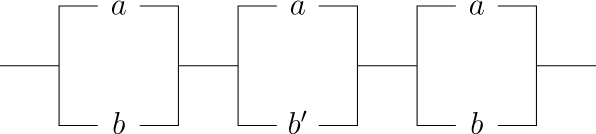
$clipboard_ebfde87e273368f1bbf2a962d8856b70e.png$

$Figure \text { } 19.32.$$(a \vee b) \wedge (a \vee b') \wedge (a \vee b)$

Історична записка

Джордж Бул (1815—1864) був першою людиною, яка вивчала решітки. У 1847 році він опублікував «Дослідження законів думки», книгу, в якій використовував решітки для формалізації логіки та обчислення пропозицій. Бул вважав, що математика - це вивчення форми, а не змісту; тобто він був не стільки стурбований тим, що він обчислює, скільки тим, як він його обчислює. Роботу Буля продовжив його друг Август Де Морган (1806—1871). Де Морган зауважив, що принцип подвійності часто тримається в теорії множин, як це ілюструють закони Де Моргана для теорії множин. Він вважав, як і Буль, що математика - це вивчення символів і абстрактних операцій.

Теорія множин і логіка надалі розвивалися такими математиками, як Альфред Норт Уайтхед (1861—1947), Бертран Рассел (1872—1970) та Девід Гільберт (1862—1943). У Principia Mathematica Уайтхед і Рассел намагалися показати зв'язок між математикою і логікою шляхом вирахування натуральної системи числення з правил формальної логіки. Якби натуральні числа можна було визначити з самої логіки, то так може і більша частина решти існуючої математики. Гільберт намагався побудувати математику, використовуючи символічну логіку таким чином, щоб довести послідовність математики. Його підходу завдав смертельний удар Куртом Геделем (1906—1978), який довів, що завжди будуть «невирішувані» проблеми в будь-якій досить багатій аксіоматичній системі; тобто, що в будь-якій математичній системі будь-якого слідства завжди знайдуться твердження, які ніколи не можуть бути доведені ні правдивими, ні помилковими.

Як часто трапляється, це фундаментальне дослідження чистої математики згодом стало незамінним у найрізноманітніших додатках. Булеві алгебри та логіка стали важливими при проектуванні великомасштабної інтегральної схеми, знайденої на сучасних комп'ютерних чіпах. Соціологи використовували решітки та булеві алгебри для моделювання соціальних ієрархій; біологи використовували їх для опису біосистем.