19.1: Грати

Last updated
Save as PDF

Page ID: 64367

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Частково впорядковані набори

Почнемо вивчення решіток і булевих алгебр з узагальнення ідеї нерівності. Нагадаємо, що відношення на множині$X$ є підмножиною$X \times X\text{.}$ A відношення$P$ на$X$ називається частковим порядком,$X$ якщо воно задовольняє наступним аксіомам.

Відношення рефлексивне:$(a, a) \in P$ для всіх$a \in X\text{.}$
Відношення антисиметричне: якщо$(a,b) \in P$ і$(b,a) \in P\text{,}$ тоді$a = b\text{.}$
Відношення є перехідним: якщо$(a, b) \in P$ і$(b, c) \in P\text{,}$ тоді$(a, c) \in P\text{.}$

Ми зазвичай$a \preceq b$ пишемо означає,$(a, b) \in P$ якщо якийсь символ природно пов'язаний з певним частковим порядком, наприклад,$a \leq b$ з цілими числами$a$$b\text{,}$ і/або$A \subset B$ з множинами,$A$$B\text{.}$ а множина$X$ разом з частковим порядком$\preceq$ є називається частково впорядкованим набором, або poset.

Приклад$19.1$

Множина цілих чисел (або раціональних або реалів) - це позиція, де

Рішення

$a \leq b$має звичайне значення для двох цілих чисел$a$ і$b$ в${\mathbb Z}\text{.}$

Приклад$19.2$

Нехай$X$ буде будь-який набір. Ми визначимо потужність набір$X$ бути множиною всіх підмножин$X\text{.}$ Ми позначимо потужність набір$X$${\mathcal P}(X)\text{.}$ за Наприклад, нехай$X = \{ a, b, c \}\text{.}$ Тоді

Рішення

${\mathcal P}(X)$є множиною всіх підмножин множини$\{ a, b, c \}\text{:}$

\ begin {align*} &\\ порожній набір &\ {a\} &\ {b\} &\ {c\} &\\\ &\ {a, b\} &\ {a, c\} &\ {b, c\} &\ {a, b, c\} &\ {a, b, c\}. &\ end {вирівнювати*}

На будь-якому силовому комплекті$X\text{,}$ встановлюють включення,$\subset\text{,}$ є частковим порядком. Ми можемо зобразити порядок на$\{ a, b, c \}$ схематично за схемою, такою, як на малюнку$19.3$.

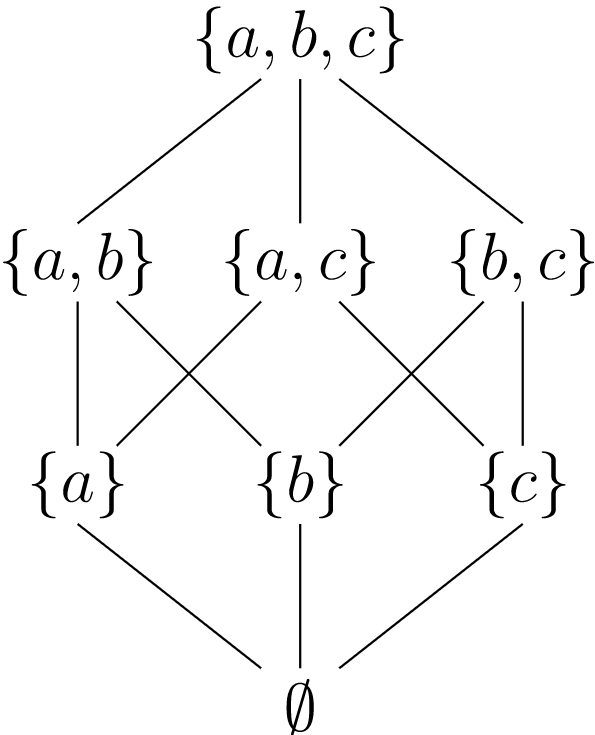
$clipboard_e1d09ee3865d3306295195b4aba0056b1.png$

$Figure \text { } 19.3.$Часткове замовлення на$\mathcal P( \{ a, b, c \})$

Приклад$19.4$

$G$Дозволяти бути групою. Множиною підгруп$G$ є a

Рішення

poset, де встановлюється частковий порядок включення.

Приклад$19.5$

На конкретному наборі може бути більше одного часткового порядку. Ми можемо сформувати частковий порядок,$a \preceq b$ якщо відношення$a \mid b\text{.}$, безумовно, є рефлексивним, оскільки$a \mid a$ для всіх$a \in {\mathbb N}\text{.}$ Якщо$m \mid n$ і$n \mid m\text{,}$ тоді.${\mathbb N}$

Рішення

$m = n\text{;}$отже, відношення також антисиметричне. Відношення є перехідним, тому що якщо$m \mid n$ і$n \mid p\text{,}$ тоді$m \mid p\text{.}$

Приклад$19.6$

$X = \{ 1, 2, 3, 4, 6, 8, 12, 24 \}$Дозволяти множина дільників$24$ з частковим порядком, визначеним у прикладі$19.5$.

Рішення

На малюнку$19.7$ показаний частковий порядок$X\text{.}$

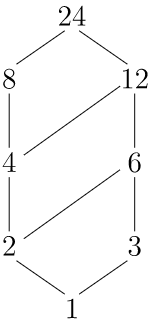
$clipboard_e099c47b3f4c6fc4ff388d9f18863e5bc.png$

$Figure \text { } 19.7.$Частковий порядок на дільники$24$

$Y$Дозволяти бути підмножиною poset$X\text{.}$ Елемент$u$ в$X$ є верхньою межею$Y$ if$a \preceq u$ для кожного елемента$a \in Y\text{.}$ If$u$ є верхньою межею$Y$ такого, що$u \preceq v$ для кожної іншої$v$ верхньої межі $Y\text{,}$то$u$ називається найменшою верхньою межею або supremum$Y\text{.}$ елемента$l$ в$X$ вважається нижньою межею$Y$ if$l \preceq a$ для всіх$a \in Y\text{.}$ If $l$є нижньою межею$Y$ такого, що$k \preceq l$ для кожної іншої$k$ нижньої межі$Y\text{,}$ потім$l$ називається найбільшою нижньою межею або нефімум$Y\text{.}$

Приклад$19.8$

$Y = \{ 2, 3, 4, 6 \}$Дозволяти міститися в$X$ наборі Приклад$19.6$. Тоді

Рішення

$Y$має верхні межі$12$ і$24\text{,}$ з$12$ як найменшою верхньою межею. Єдина нижня межа,$1\text{;}$ отже, вона повинна бути найбільшою нижньою мемою.

Як виявляється, найменші верхні межі і найбільші нижні межі унікальні, якщо вони існують.

Теорема$19.9$

$Y$Дозволяти бути непорожньою підмножиною poset$X\text{.}$ Якщо$Y$ має найменшу верхню межу, то$Y$ має унікальну найменшу верхню межу. Якщо$Y$ має найбільшу нижню межу, то$Y$ має унікальну найбільшу нижню межу.

Доказ: $u_1$$u_2$Дозволяти і бути найменш верхні межі для$Y\text{.}$ За визначенням найменшої верхньої межі$u$,$u_1 \preceq u$ для всіх верхніх меж$Y\text{.}$ Зокрема,$u_1 \preceq u_2\text{.}$ Аналогічно,$u_2 \preceq u_1\text{.}$ Отже,$u_1 = u_2$ антисиметрія. Подібний аргумент показує, що найбільша нижня межа унікальна.

На багатьох постах можна визначити бінарні операції, використовуючи найбільшу нижню межу та найменшу верхню межу двох елементів. Решітка - це$L$ така позиція, що кожна пара елементів$L$ має найменшу верхню межу та найбільшу нижню межу. Найменша верхня межа$a, b \in L$ називається$a$ з'єднанням$b$ і і позначається$a \vee b\text{.}$ Найбільша нижня межа$a, b \in L$ називається $a$зустріччю$b$ і і позначається$a \wedge b\text{.}$

Приклад$19.10$

Нехай$X$ буде набір. Тоді набір потужності$X\text{,}$${\mathcal P}(X)\text{,}$ - це решітка. На два комплекти

Рішення

$A$і$B$ в${\mathcal P}(X)\text{,}$ найменшій верхній межі$A$ і$B$ є$A \cup B\text{.}$ Звичайно,$A \cup B$ є верхньою межею$A$ і$B\text{,}$ так$A \subset A \cup B$ і$B \subset A \cup B\text{.}$ Якщо$C$ якийсь інший набір, що містить обидва,$A$ а$B\text{,}$ потім $C$повинен містити,$A \cup B\text{;}$ отже,$A \cup B$ є найменшою верхньою межею$A$ і$B\text{.}$ Аналогічно, найбільша нижня$A$ межа і$B$ є$A \cap B\text{.}$

Приклад$19.11$

$G$Дозволяти бути групою і припустимо, що$X$ це множина підгруп$G\text{.}$ Тоді

Рішення

$X$це посада, упорядкована множинно-теоретичним$\subset\text{.}$ включенням, множина підгруп також$G$ є решіткою. Якщо$H$ і$K$ є підгрупами найбільшої нижньої межі$H$ і$K$ є$H \cap K\text{.}$ Множина не$H \cup K$ може бути підгрупою$G\text{.}$ Ми залишаємо це як вправу, щоб показати, що найменша верхня$H$ межа і$K$ є підгрупою, що генерується$G\text{,}$ $H \cup K\text{.}$

У теорії множин ми маємо певні умови подвійності. Наприклад, згідно із законами Де Моргана, будь-яке твердження про множини, яке є правдою, також$(A \cup B)'$ має бути правдою щодо$A' \cap B'\text{.}$ Ми також маємо принцип подвійності для решіток.

Аксіома$19.12$. Principle of Duality

Будь-яке твердження, яке є істинним для всіх решіток, залишається істинним, коли$\preceq$$\succeq$ його замінюють$\vee$ і$\wedge$ змінюються у всьому твердженні.

Наступна теорема говорить нам, що решітка - це алгебраїчна структура з двома бінарними операціями, які задовольняють певним аксіомам.

Теорема$19.13$

Якщо$L$ є решіткою, то двійкові операції$\vee$ і$\wedge$ задовольняють наступні властивості для$a, b, c \in L\text{.}$

Комутативні$a \vee b = b \vee a$ закони: і$a \wedge b = b \wedge a\text{.}$
Асоціативні$a \vee ( b \vee c) = (a \vee b) \vee c$ закони: і$a \wedge (b \wedge c) = (a \wedge b) \wedge c\text{.}$
Ідемпотентні$a \vee a = a$ закони: і$a \wedge a = a\text{.}$
Закони поглинання:$a \vee (a \wedge b) = a$ і$a \wedge ( a \vee b ) =a\text{.}$

Доказ

За принципом подвійності нам потрібно лише довести перше твердження в кожній частині.

(1) За визначенням$a \vee b$ є найменшою верхньою межею$\{ a, b\}\text{,}$ і$b \vee a$ є найменшою верхньою межею$\{ b, a \}\text{;}$ проте,$\{ a, b\} = \{ b, a \}\text{.}$

(2) Ми покажемо, що$a \vee ( b \vee c)$ і$(a \vee b) \vee c$ є найменшими верхніми межами$\{ a, b, c \}\text{.}$ Нехай$d = a \vee b\text{.}$ тоді$c \preceq d \vee c = (a \vee b) \vee c\text{.}$ Ми також знаємо, що

\[ a \preceq a \vee b =d \preceq d \vee c = (a \vee b) \vee c\text{.} \nonumber \]

Аналогічний аргумент демонструє, що$b \preceq (a \vee b) \vee c\text{.}$ Отже,$(a \vee b) \vee c$ є верхньою межею$\{ a, b, c \}\text{.}$ Ми тепер повинні показати, що$(a \vee b) \vee c$ є найменшою верхньою межею$\{ a, b, c\}\text{.}$$u$ Дозволяти бути деякою іншою верхньою межею$\{ a, b, c \}\text{.}$ Тоді$a \preceq u$ і,$b \preceq u\text{;}$ отже,$d = a \vee b \preceq u\text{.}$ Так як$c \preceq u\text{,}$ вона випливає, що$(a \vee b) \vee c = d \vee c \preceq u\text{.}$ Отже,$(a \vee b) \vee c$ повинна бути найменшою верхньою$\{ a, b, c\}\text{.}$ межею аргументу, який показує,$a \vee ( b \vee c)$ є найменшою верхньою$\{ a, b, c \}$ межею того ж. Отже,$a \vee ( b \vee c) = (a \vee b) \vee c\text{.}$

(3) З'єднання$a$ і$a$ є найменшою верхньою межею$\{ a \}\text{;}$ звідси,$a \vee a = a\text{.}$

(4) Нехай$d = a \wedge b\text{.}$ Тоді$a \preceq a \vee d\text{.}$ З іншого боку,$d = a \wedge b \preceq a\text{,}$ і$a \vee d \preceq a\text{.}$ тому,$a \vee ( a \wedge b) = a\text{.}$

З огляду на будь-яку довільну множину$L$ з операціями$\vee$ і$\wedge\text{,}$ задовольняє умовам попередньої теореми, закономірно запитати, чи походить ця множина з якоїсь решітки. Наступна теорема говорить про те, що це завжди так.

Теорема$19.14$

$L$Дозволяти бути непорожнім множиною з двома бінарними операціями$\vee$ і$\wedge$ задовольняє комутативний, асоціативний, ідемпотентний і поглинання законів. Ми можемо визначити частковий порядок$L$ на,$a \preceq b$ якщо$a \vee b = b\text{.}$ Крім того,$L$ є решіткою щодо$\preceq$ якщо для всіх$a, b \in L\text{,}$ ми визначаємо найменшу верхню межу та найбільшу нижню межу. від$a$ $a \vee b$і$b$$a \wedge b\text{,}$ відповідно.

Доказ

Ми спочатку показуємо, що$L$ є poset під$\preceq\text{.}$ Since$a \vee a = a\text{,}$$a \preceq a$ і$\preceq$ є рефлексивним. Щоб показати, що$\preceq$ є антисиметричним, нехай$a \preceq b$ і$b \preceq a\text{.}$ тоді$a \vee b = b$ і$b \vee a = a\text{.}$ за комутативним законом,$b = a \vee b = b \vee a = a\text{.}$ Нарешті, ми повинні показати, що$\preceq$ є перехідним. Нехай$a \preceq b$ і$b \preceq c\text{.}$ тоді$a \vee b = b$ і$b \vee c = c\text{.}$ таким чином,

\[ a \vee c = a \vee (b \vee c ) = ( a \vee b) \vee c = b \vee c = c\text{,} \nonumber \]

або$a \preceq c\text{.}$

Щоб показати, що$L$ це решітка, ми повинні довести, що$a \vee b$ і$a \wedge b$ є, відповідно, найменшою верхньою і найбільшою нижньою межею$a$ і$b\text{.}$ Оскільки$a=(a \vee b) \wedge a = a \wedge (a \vee b)\text{,}$ випливає, що$a \preceq a \vee b\text{.}$ Аналогічно,$b \preceq a \vee b\text{.}$ Отже,$a \vee b$ є верхньою межею для$a$ і $b\text{.}$$u$Дозволяти будь-яка інша верхня межа обох$a$ і$b\text{.}$ Тоді$a \preceq u$ і$b \preceq u\text{.}$ Але$a \vee b \preceq u$ так як

\[ (a \vee b) \vee u = a \vee (b \vee u) = a \vee u = u\text{.} \nonumber \]

Доказ того, що$a \wedge b$ є найбільшою нижньою$a$$b$ межею і залишається як вправа.