8.2: Виявлення помилок та виправлення кодів

Розберемо просту модель системи зв'язку для передачі і прийому кодованих повідомлень (рис.\(8.1\)).

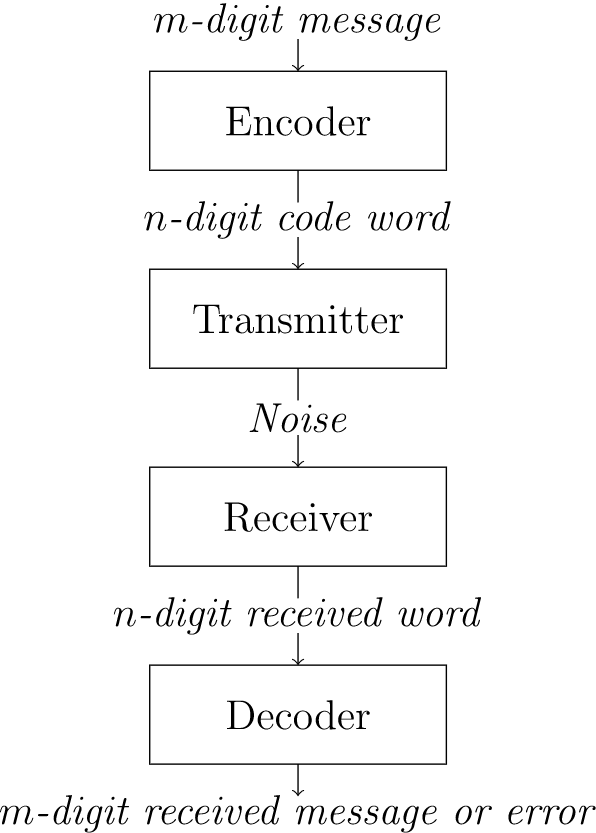
\(Figure \text { } 8.1.\)Кодування і декодування повідомлень

Некодовані повідомлення можуть складатися з букв або символів, але зазвичай вони складаються з двійкових\(m\) -кортежів. Ці повідомлення кодуються в кодові слова, що складаються з двійкових\(n\) -кортежів, пристроєм, званим кодером. Повідомлення передається, а потім декодується. Ми розглянемо виникнення помилок при передачі. Помилка виникає при зміні одного або декількох бітів в кодовому слові. Схема декодування - це метод, який або перетворює довільно отриманий\(n\) -кортеж у значуще декодоване повідомлення або видає повідомлення про помилку для цього\(n\) -кортежу. Якщо отримане повідомлення є кодовим словом (один зі спеціальних\(n\) -кортежів, дозволених до передачі), то декодованим повідомленням має бути унікальне повідомлення, яке було закодовано в кодове слово. Для отриманих некодових слів схема декодування дасть вказівку на помилку, або, якщо ми більш розумні, насправді спробуємо виправити помилку і реконструювати вихідне повідомлення. Наша мета - максимально дешево і швидко передавати повідомлення без помилок.

Приклад\(8.2\)

Однією з можливих схем кодування було б відправити повідомлення кілька разів і порівняти отримані копії один з одним. Припустимо, що кодується повідомлення є двійковим\(n\)\((x_{1}, x_{2}, \ldots, x_{n})\text{.}\) -кортежем. Повідомлення кодується в двійковий\(3n\) -кортеж простим повторенням повідомлення тричі:

\[ (x_{1}, x_{2}, \ldots, x_{n}) \mapsto (x_{1}, x_{2}, \ldots, x_{n}, x_{1}, x_{2}, \ldots, x_{n}, x_{1}, x_{2}, \ldots, x_{n})\text{.} \nonumber \]

Рішення

Щоб розшифрувати повідомлення, вибираємо в якості\(i\) ї цифри ту, яка з'являється в\(i\) -му місці хоча б в двох з трьох передач. Наприклад, якщо вихідне повідомлення,\((0110)\text{,}\) то передане повідомлення буде\((0110\; 0110\; 0110)\text{.}\) Якщо є помилка передачі в п'ятій цифрі, то отримане кодове слово буде,\((0110\; 1110\; 0110)\text{,}\) яке буде коректно декодовано як\((0110)\text{.}\) ³ Цей метод потрійного повторення буде автоматично виявити і виправити всі поодинокі помилки, але це повільно і неефективно: для відправки повідомлення, що складається з\(n\) бітів, потрібні\(2n\) зайві біти, і ми можемо тільки виявити і виправити поодинокі помилки. Ми побачимо, що можна знайти схему кодування, яка буде кодувати повідомлення\(n\) бітів в\(m\) біти з\(m\) набагато меншими ніж\(3n\text{.}\)

Приклад\(8.3\)

Навіть парність, часто використовувана схема кодування, набагато ефективніше, ніж проста схема повторення. Система кодування ASCII (Американський стандартний код обміну інформацією) використовує двійкові\(8\) -кортежі, що дає\(2^{8} = 256\) можливі\(8\) -кортежі. Однак потрібні лише сім біт, оскільки є лише символи\(2^7 = 128\) ASCII. Що можна або потрібно зробити з додатковим бітом?

Рішення

Використовуючи повні вісім біт, ми можемо виявити помилки одиночної передачі. Наприклад, ASCII коди для A, B і C є

\ почати {вирівнювати*}\ текст {A} & = 65_ {10} = 01000001_ {2},\\ текст {B} & = 66_ {10} = 01000010_ {2},\\ текст {C} & = 67_ {10} = 01000011_ {2}\ текст {.} \ end {вирівнювати*}

Зверніть увагу, що крайній лівий біт завжди встановлений на 0; тобто символи\(128\) ASCII мають коди

\ почати {вирівнювати*} 00000000_ {2} & = 0_ {10},\\ &\ vdots\\ 01111111_ {2} & = 127_ {10}\ текст {.} \ end {вирівнювати*}

Біт можна використовувати для перевірки помилок на інших семи бітах. Встановлюється\(0\) або\(1\) так, щоб загальна кількість\(1\) бітів у поданні символу була парною. Використовуючи парність парності, коди для A, B і C тепер стають

\ почати {вирівнювати*}\ текст {A} & = 01000001_ {2},\\ текст {B} & = 01000010_ {2},\\ текст {C} & = 11000011_ {2}\ текст {.} \ end {вирівнювати*}

Припустимо, відправляється A і помилка передачі в шостому біті викликана шумом над каналом зв'язку так, що\((0100\; 0101)\) приймається. Ми знаємо, що сталася помилка, оскільки отримане слово має непарну кількість\(1\) s, і тепер ми можемо вимагати, щоб кодове слово було передано знову. При використанні для перевірки помилок крайній лівий біт називається бітом перевірки парності.

На сьогоднішній день найпоширеніші коди виявлення помилок, що використовуються в комп'ютерах, засновані на додаванні біта парності. Як правило, комп'ютер зберігає інформацію в\(m\) -кортежах, званих словами. Загальні довжини слів є\(8\text{,}\)\(16\text{,}\) і\(32\) біти. Один біт у слові відводиться як біт перевірки парності, і не використовується для зберігання інформації. Цей біт встановлюється\(0\) або в\(1\text{,}\) залежності від кількості\(1\) s у слові.

Додавання біта перевірки парності дозволяє виявити всі поодинокі помилки, оскільки зміна одного біта або збільшує або зменшує кількість\(1\) s на одиницю, і в будь-якому випадку парність була змінена з парної на непарну, тому нове слово не є кодовим словом. (Ми також могли б побудувати схему виявлення помилок на основі непарної парності; тобто ми могли б встановити біт перевірки парності так, що кодове слово завжди має непарну кількість\(1\) s.)

Рівна система парності проста в реалізації, але має два недоліки. По-перше, множинні помилки не виявляються. Припустимо, відправляється A і перший і сьомий біти змінені з\(0\) на Отримане слово є кодовим словом, але буде декодовано в C замість A. Second, у нас немає можливості виправити помилки.\(1\text{.}\) Якщо\((1001\; 1000)\) 8-кортеж отримано, ми знаємо, що сталася помилка, але ми поняття не маємо, який біт був змінений. Зараз ми будемо досліджувати схему кодування, яка не тільки дозволить нам виявити помилки передачі, але й фактично виправити помилки.

Приклад\(8.4\)

Припустимо, що наше оригінальне повідомлення є\(0\) або a,\(1\text{,}\) і яке\(0\) кодує\((000)\) і\(1\) кодує в\((111)\text{.}\)

Рішення

Якщо під час передачі виникає лише одна помилка, ми можемо виявити та виправити помилку. Наприклад, якщо отримано a\((101)\), то другий біт повинен бути змінений з a на a\(1\) Первісно передане кодове слово повинно бути.\((111)\text{.}\) Цей метод виявить і виправляє всі поодинокі помилки.\(0\text{.}\)

\(Table \text { } 8.5\). Код повторення

Передано	Отримане слово
Кодове слово	\(000\)	\(001\)	\(010\)	\(011\)	\(100\)	\(101\)	\(110\)	\(111\)
\(000\)	\(0\)	\(1\)	\(1\)	\(2\)	\(1\)	\(2\)	\(2\)	\(3\)
\(111\)	\(3\)	\(2\)	\(2\)	\(1\)	\(2\)	\(1\)	\(1\)	\(0\)

У таблиці ми представляємо всі можливі слова\(8.5\), які можуть бути отримані для переданих кодових слів,\((000)\) а\((111)\text{.}\) Таблиця\(8.5\) також показує кількість бітів, якими кожен отриманий\(3\) -кортеж відрізняється від кожного вихідного кодового слова.

Розшифровка з максимальною ймовірністю

Схема кодування, представлена в прикладі, не\(8.4\) є повноцінним рішенням проблеми, оскільки вона не враховує можливість множинних помилок. Наприклад, або (000) або (111) може бути відправлений і (001) отриманий. У нас немає засобів вирішити з отриманого слова, чи була одна помилка в третьому біті або дві помилки, одна в першому біті і одна в другому. Незалежно від того, яка схема кодування використовується, може бути отримано некоректне повідомлення. Ми могли б передати (000), мати помилки у всіх трьох бітах, і отримати кодове слово (111). Важливо зробити явні припущення щодо ймовірності та розподілу помилок передачі, щоб в конкретному додатку було відомо, чи підходить дана схема виявлення помилок. Будемо вважати, що помилки передачі рідкісні, і, що коли вони відбуваються, вони відбуваються незалежно в кожному біті;\(p\) тобто якщо ймовірність помилки в одному біті і\(q\) є ймовірність помилки в іншому біті, то ймовірність виникнення помилок в обох цих бітах в той же час є\(pq\text{.}\) Ми також будемо вважати, що отриманий\(n\) -кортеж декодується в кодове слово, яке найближче до нього; тобто ми припускаємо, що приймач використовує декодування з максимальною ймовірністю. ⁴

Цей розділ вимагає знання ймовірності, але його можна пропустити без втрати безперервності.

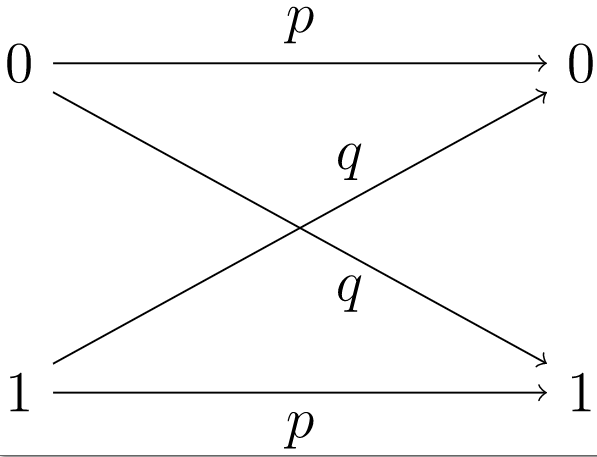
\(Figure \text { } 8.6.\)Двійковий симетричний канал

Двійковий симетричний канал - це модель, яка складається з передавача, здатного надсилати двійковий сигнал,\(0\) або a\(1\text{,}\) разом з приймачем. \(p\)Дозволяти ймовірність того, що сигнал правильно прийнятий. Тоді\(q = 1 - p\) є ймовірність неправильного прийому. Якщо\(1\) відправляється a, то ймовірність того, що a\(1\) отримано, є\(p\) і ймовірність того, що a отримано\(0\) дорівнює\(q\) (рис.\(8.6\)). Імовірність того, що ніяких помилок при передачі двійкового кодового слова довжини\(n\) не виникає.\(p^{n}\text{.}\) Наприклад, якщо\(p=0.999\) і відправляється повідомлення, що складається з 10 000 біт, то ймовірність ідеальної передачі дорівнює

\[ (0.999)^{10,000} \approx 0.00005\text{.} \nonumber \]

Теорема\(8.7\)

Якщо двійковий\(n\) -кортеж\((x_{1}, \ldots, x_{n})\) передається по двійковому симетричному каналу з ймовірністю\(p\), що в кожній координаті не виникне помилки, то ймовірність того, що в точності\(k\) координати є помилки, дорівнює

\[ \binom{n}{k} q^kp^{n - k}\text{.} \nonumber \]

Доказ

Виправте\(k\) різні координати. Спочатку обчислюємо ймовірність того, що сталася помилка в цьому фіксованому наборі координат. Імовірність помилки, що виникає в певній одній з цих\(k\) координат, - це\(q\text{;}\) ймовірність того, що помилка не відбудеться ні в одній з інших\(n-k\) координат є\(p\text{.}\) Імовірність кожного з цих\(n\) незалежних подій\(q^{k}p^{n-k}\text{.}\) дорівнює числу можливі шаблони\(k\) помилок з точно виникаючими помилками дорівнює

\[ \binom{n}{k} = \frac{n!}{k!(n - k)!}\text{,} \nonumber \]

кількість комбінацій\(n\) речей, прийнятих\(k\) за один раз. Кожен з цих шаблонів помилок має ймовірність\(q^{k}p^{n-k}\) виникнення; отже, ймовірність всіх цих шаблонів помилок є

\[ \binom{n}{k} q^{k}p^{n - k}\text{.} \nonumber \]

Приклад\(8.8\)

Припустимо, що\(p = 0.995\) і\(500\) -bit повідомлення надіслано.

Рішення

Імовірність того, що повідомлення було надіслано без помилок, становить

\[ p^{n} = (0.995)^{500} \approx 0.082\text{.} \nonumber \]

Імовірність виникнення рівно однієї помилки дорівнює

\[ \binom{n}{1} qp^{n - 1}= 500(0.005)(0.995)^{499} \approx 0.204\text{.} \nonumber \]

Імовірність рівно двох помилок дорівнює

\[ \binom{n}{2} q^{2}p^{n - 2}= \frac{500 \cdot 499}{2}(0.005)^{2}(0.995)^{498} \approx 0.257\text{.} \nonumber \]

Імовірність появи більше двох помилок приблизно

\[ 1 - 0.082 - 0.204 - 0.257 = 0.457\text{.} \nonumber \]

Блокові коди

Якщо ми хочемо розробити ефективні коди виявлення помилок та виправлення помилок, нам знадобляться більш складні математичні інструменти. Теорія груп дозволить прискорити методи кодування і декодування повідомлень. Кодом називається\((n, m)\) - блоковий код, якщо інформація, яка підлягає кодуванню, може бути розділена на блоки\(m\) двійкових цифр, кожен з яких може бути закодований в\(n\) двійкові цифри. Більш конкретно, код\((n, m)\) -block складається з функції кодування

\[ E:{\mathbb Z}^{m}_{2} \rightarrow {\mathbb Z}^{n}_{2} \nonumber \]

і функція декодування

\[ D:{\mathbb Z}^{n}_{2} \rightarrow {\mathbb Z}^{m}_{2}\text{.} \nonumber \]

Кодове слово - це будь-який елемент зображення\(E\text{.}\) Ми також вимагаємо, щоб\(E\) бути один-на-один, щоб два інформаційні блоки не були закодовані в одному кодовому слові. Якщо наш код буде виправляти помилки, то\(D\) повинен бути на.

Приклад\(8.9\)

Система кодування парності, розроблена для виявлення одиночних помилок в символах ASCII, є кодом\((8,7)\) -block.

Рішення

Функція кодування

\[ E(x_7, x_6, \ldots, x_1) = (x_8, x_7, \ldots, x_1)\text{,} \nonumber \]

де\(x_8 = x_7 + x_6 + \cdots + x_1\) з додаванням в\({\mathbb Z}_2\text{.}\)

\({\mathbf y} = (y_1, \ldots, y_n)\)Дозволяти\({\mathbf x} = (x_1, \ldots, x_n)\) і бути\(n\) двійковими -кортежами. Відстань Хеммінга або відстань,\(d({\mathbf x}, {\mathbf y})\text{,}\) між\({\mathbf x}\) і\({\mathbf y}\) - це кількість бітів, в яких\({\mathbf x}\) і\({\mathbf y}\) відрізняються. Відстань між двома кодовими словами - це мінімальна кількість помилок передачі, необхідних для зміни одного кодового слова в інше. Мінімальна відстань для коду\(d_{\min}\text{,}\) - це мінімум усіх відстаней,\(d({\mathbf x}, {\mathbf y})\text{,}\) де\({\mathbf x}\) і\({\mathbf y}\) є різними кодовими словами. Вага\(w({\mathbf x})\text{,}\) двійкового кодового слова\({\mathbf x}\) - це кількість\(1\) s в\({\mathbf x}\text{.}\) Ясно,\(w({\mathbf x}) = d({\mathbf x}, {\mathbf 0})\text{,}\) де\({\mathbf 0} = (00 \cdots 0)\text{.}\)

Приклад\(8.10\)

Дозвольте\({\mathbf x} = (10101)\text{,}\)\({\mathbf y} = (11010)\text{,}\) і\({\mathbf z} = (00011)\) бути всі кодові слова в якомусь коді\(C\text{.}\)

Рішення

Тоді у нас є такі відстані Хеммінга:

\[ d({\mathbf x},{\mathbf y}) = 4, \qquad d({\mathbf x},{\mathbf z}) = 3, \qquad d({\mathbf y},{\mathbf z}) = 3\text{.} \nonumber \]

Мінімальна відстань для цього коду - 3. У нас також є такі ваги:

\[ w({\mathbf x}) = 3, \qquad w({\mathbf y}) = 3, \qquad w({\mathbf z}) = 2\text{.} \nonumber \]

У наступній пропозиції перераховані деякі основні властивості щодо ваги кодового слова та відстані між двома кодовими словами. Доказ залишають як вправу.

Пропозиція\(8.11\)

\({\mathbf z}\)Дозволяти\({\mathbf x}\text{,}\)\({\mathbf y}\text{,}\) і бути\(n\) двійковими -кортежами. Тоді

1. \(w({\mathbf x}) = d( {\mathbf x}, {\mathbf 0})\text{;}\)
2. \(d( {\mathbf x}, {\mathbf y}) \geq 0\text{;}\)
3. \(d( {\mathbf x}, {\mathbf y}) = 0\)саме коли\({\mathbf x} = {\mathbf y}\text{;}\)
4. \(d( {\mathbf x}, {\mathbf y})= d( {\mathbf y}, {\mathbf x})\text{;}\)
5. \(d( {\mathbf x}, {\mathbf y}) \leq d( {\mathbf x}, {\mathbf z}) + d( {\mathbf z}, {\mathbf y})\text{.}\)

\(Table \text { } 8.12.\)Відстані між 4-бітними кодовими словами

	\(0000\)	\(0011\)	\(0101\)	\(0110\)	\(1001\)	\(1010\)	\(1100\)	\(1111\)
\(0000\)	\(0\)	\(2\)	\(2\)	\(2\)	\(2\)	\(2\)	\(2\)	\(4\)
\(0011\)	\(2\)	\(0\)	\(2\)	\(2\)	\(2\)	\(2\)	\(4 \)	\(2\)
\(0101\)	\(2\)	\(2\)	\(0\)	\(2\)	\(2\)	\(4\)	\(2\)	\(2\)
\(0110\)	\(2\)	\(2\)	\(2\)	\(0\)	\(4\)	\(2\)	\(2\)	\(2\)
\(1001\)	\(2\)	\(2\)	\(2\)	\(4\)	\(0\)	\(2\)	\(2\)	\(2\)
\(1010\)	\(2\)	\(2\)	\(4\)	\(2\)	\(2\)	\(0\)	\(2\)	\(2\)
\(1100\)	\(2\)	\(4\)	\(2\)	\(2\)	\(2\)	\(2\)	\(0\)	\(2\)
\(1111\)	\(4\)	\(2\)	\(2\)	\(2\)	\(2\)	\(2\)	\(2\)	\(0\)

Ваги в конкретному коді, як правило, набагато простіше обчислити, ніж відстані Хеммінга між усіма кодовими словами в коді. Якщо код налаштований ретельно, ми можемо використовувати цей факт на нашу користь.

Припустимо, що\({\mathbf x} = (1101)\) і\({\mathbf y} = (1100)\) є кодовими словами в якомусь коді. Якщо ми передаємо\((1101)\) і виникне помилка в крайньому правому біті, то (1100) буде отримано. Оскільки\((1100)\) це кодове слово, декодер буде декодувати\((1100)\) як передане повідомлення. Цей код явно не дуже підходить для виявлення помилок. Проблема полягає в тому, що\(d({\mathbf x}, {\mathbf y}) = 1\text{.}\) якщо\({\mathbf x} = (1100)\) і\({\mathbf y} = (1010)\) є кодовими словами, то\(d({\mathbf x}, {\mathbf y}) = 2\text{.}\) Якщо\({\mathbf x}\) передається і виникає одна помилка, то ніколи не\({\mathbf y}\) може бути отримана. Таблиця\(8.12\) дає відстані між усіма 4-бітними кодовими словами, в яких перші три біти несуть інформацію, а четвертий - парний біт перевірки парності. Ми бачимо, що мінімальна відстань тут,\(2\text{;}\) отже, код підходить як єдиний код виявлення помилок.

Щоб точно визначити, якими є можливості виявлення помилок та виправлення помилок для коду, нам потрібно проаналізувати мінімальну відстань для коду. \({\mathbf y}\)Дозволяти\({\mathbf x}\) і бути кодовими словами. Якщо\(d({\mathbf x}, {\mathbf y}) = 1\) і виникає помилка де\({\mathbf x}\) і\({\mathbf y}\) відрізняються, то\({\mathbf x}\) змінюється на\({\mathbf y}\text{.}\) Отримане кодове слово є\({\mathbf y}\) і не видається повідомлення про помилку. Тепер припустимо\(d({\mathbf x}, {\mathbf y}) = 2\text{.}\) Тоді одна помилка не може\({\mathbf x}\) змінитися на\({\mathbf y}\text{.}\) Тому, якщо у\(d_{\min} = 2\text{,}\) нас є можливість виявляти окремі помилки. Однак припустимо, що\(d({\mathbf x}, {\mathbf y}) = 2\text{,}\)\({\mathbf y}\) відправлено, і некодове слово отримано\({\mathbf z}\) таке, що

\[ d({\mathbf x}, {\mathbf z}) = d({\mathbf y}, {\mathbf z}) = 1\text{.} \nonumber \]

Тоді декодер не може вирішити між ними\({\mathbf x}\) і\({\mathbf y}\text{.}\) Незважаючи на те, що ми знаємо, що сталася помилка, ми не знаємо, що таке помилка.

Припустимо,\(d_{\min} \geq 3\text{.}\) тоді схема декодування з максимальною ймовірністю виправляє всі поодинокі помилки. Починаючи з кодового слова,\({\mathbf x}\text{,}\) помилка при передачі одного біта дає\({\mathbf y}\) з,\(d({\mathbf x}, {\mathbf y}) = 1\text{,}\) але\(d({\mathbf z}, {\mathbf y}) \geq 2\) для будь-якого іншого кодового слова.\({\mathbf z} \neq {\mathbf x}\text{.}\) Якщо ми не вимагаємо виправлення помилок, то ми можемо виявити кілька помилок, коли код має мінімальну відстань, яка більше або дорівнює до\(3\text{.}\)

Теорема\(8.13\)

\(C\)Дозволяти код з\(d_{\min} = 2n + 1\text{.}\) Потім\(C\) може виправити будь-які\(n\) або менше помилок. Крім того, будь-які\(2n\) або менше помилок можуть бути виявлені в\(C\text{.}\)

Доказ

Припустимо,\({\mathbf x}\) що надіслано кодове слово і\({\mathbf y}\) слово отримано з максимальною кількістю\(n\) помилок. Тоді\(d( {\mathbf x}, {\mathbf y}) \leq n\text{.}\) Якщо\({\mathbf z}\) є будь-яке кодове слово, крім\({\mathbf x}\text{,}\) тоді

\[ 2n+1 \leq d( {\mathbf x}, {\mathbf z}) \leq d( {\mathbf x}, {\mathbf y}) + d( {\mathbf y}, {\mathbf z}) \leq n + d( {\mathbf y}, {\mathbf z})\text{.} \nonumber \]

Отже,\(d({\mathbf y}, {\mathbf z} ) \geq n+1\) і\({\mathbf y}\) буде правильно розшифрований як\({\mathbf x}\text{.}\) Тепер припустимо, що\({\mathbf x}\) передається і отримано і що сталася хоча б одна помилка, але не більше\(2n\) помилок.\({\mathbf y}\) Тоді\(1 \leq d( {\mathbf x}, {\mathbf y} ) \leq 2n\text{.}\) оскільки мінімальна відстань між кодовими словами не\(2n +1\text{,}\)\({\mathbf y}\) може бути кодовим словом. Отже, код може виявляти між\(1\) і\(2n\) помилки.

Приклад\(\PageIndex{1}\)

У таблиці\(8.15\) кодові слова\({\mathbf c}_1 = (00000)\text{,}\)\({\mathbf c}_2 = (00111)\text{,}\)\({\mathbf c}_3 = (11100)\text{,}\) і\({\mathbf c}_4 = (11011)\) визначають єдиний код виправлення помилок.

Рішення

\(Table \text { } 8.15.\)Відстані Хеммінга для коду, що виправляє помилки

	\(00000\)	\(00111\)	\(11100\)	\(11011\)
\(00000 \)	\(0\)	\(3\)	\(3\)	\(4\)
\(00111 \)	\(3\)	\(0\)	\(4\)	\(3\)
\(11100 \)	\(3\)	\(4\)	\(0\)	\(3\)
\(11011 \)	\(4\)	\(3\)	\(3\)	\(0\)

Історична записка

Сучасна теорія кодування почалася в 1948 році з статті К.Шеннона «Математична теорія інформації» [7]. Цей документ запропонував приклад алгебраїчного коду, і теорема Шеннона проголосила, наскільки хороші коди можна очікувати. Річард Хеммінг почав працювати з лінійними кодами в Bell Labs наприкінці 1940-х і початку 1950-х років після того, як став розчарований, тому що програми, які він запускав, не могли відновити від простих помилок, породжених шумом. Теорія кодування надзвичайно зросла за останні кілька десятиліть. Теорія кодів, що виправляють помилки, МакВільямс і Слоун [5], опублікована в 1977 році, вже містила понад 1500 посилань. Лінійні коди (коди Ріда-Муллера\((32, 6)\) -блок) використовувалися на космічних зондах NASA Mariner. Більш пізні космічні зонди, такі як Voyager, використовували те, що називаються кодами згортки. В даний час проводяться дуже активні дослідження з кодами Гоппа, які сильно залежать від алгебраїчної геометрії.