1.5: Теорема Піфагора для площі та периметра
- Page ID
- 54772
Знайти відсутні сторони, щоб обчислити площу
Застосування теореми Піфагора
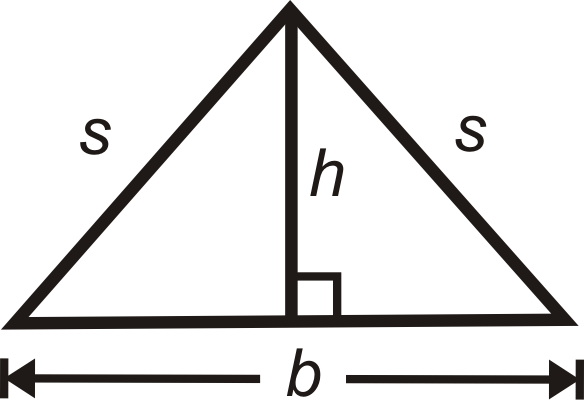
Знайти висоту рівнобедреного трикутника
Один із способів використання теореми Піфагора - знайти висоту рівнобедреного трикутника (див. Приклад 1).
Доведіть формулу відстані
Ще одним застосуванням теореми Піфагора є формула відстані. Доведемо це тут.
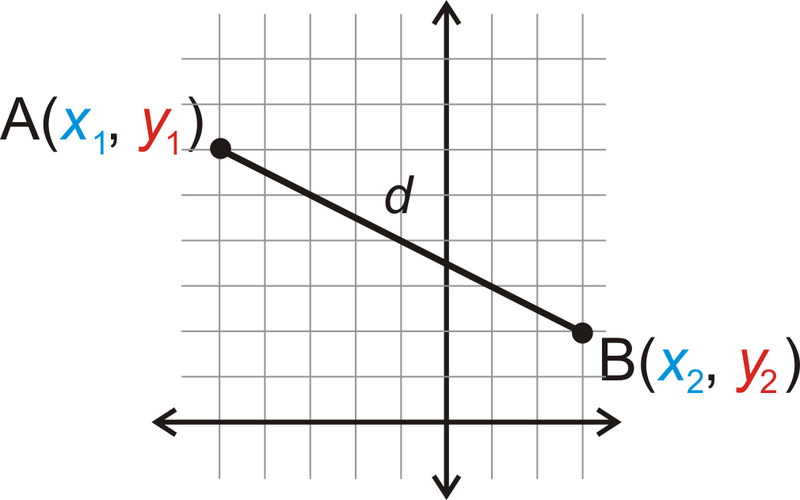
Почнемо з точки\(A(x_1, y_1)\) і точки\(B(x_2, y_2)\). Ми будемо називати відстань між A і B, d.
Намалюйте вертикальну і горизонтальну довжини, щоб вийшов прямокутний трикутник.
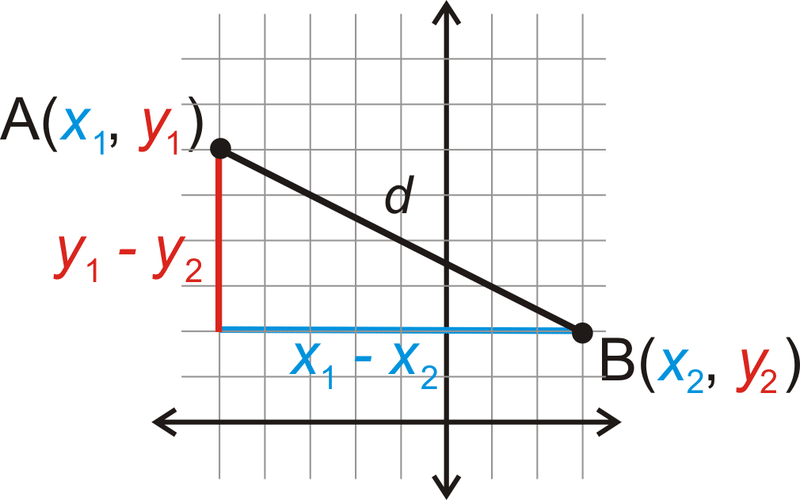
Тепер, коли у нас є прямокутний трикутник, ми можемо використовувати теорему Піфагора, щоб знайти гіпотенузу, d.
\(\begin{aligned} d^2&=\sqrt{(x_1−x_2)^2+(y_1−y_2)^2} \\ d&=(x_1−x_2)^2+(y_1−y_2)^2 \end{aligned}\)
Формула відстані: відстань між\(A(x_1,y_1)\) і\(B(x_2,y_2)\) є
\(d=\sqrt{(x_1−x_2)^2+(y_1−y_2)^2}\).
Класифікувати трикутник як гострий, правий або тупий
Ми можемо розширити зворотне теореми Піфагора, щоб визначити, чи трикутник є тупим або гострим трикутником.
Гострі трикутники: Якщо сума квадратів двох коротших сторін прямокутного трикутника більша за квадрат найдовшої сторони, то трикутник гострий.
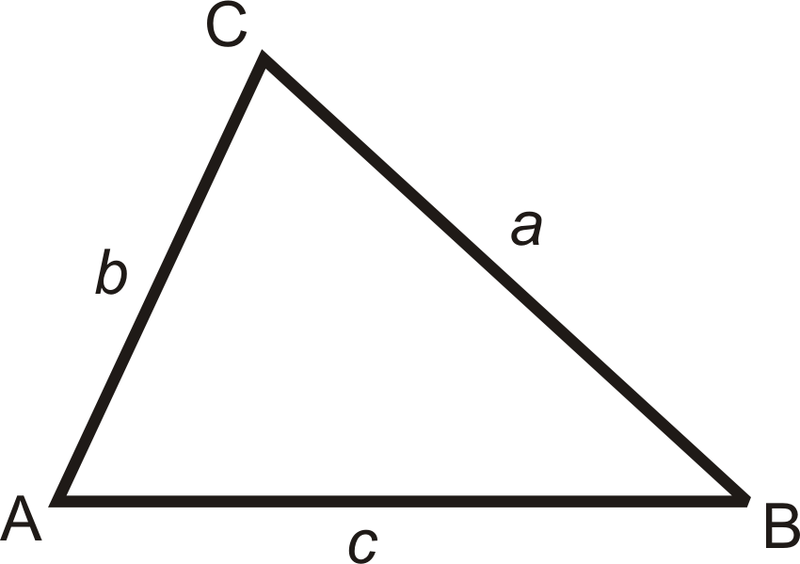
Для\(b<c\) і\(a<c\), якщо\(a^2+b^2>c^2\), то трикутник гострий.
Тупі трикутники: Якщо сума квадратів двох коротших сторін прямокутного трикутника менше квадрата найдовшої сторони, то трикутник тупий.
Для\(b<c\) і\(a<c\), якщо\(a^2+b^2<c^2\), то трикутник тупий.
Що робити, якщо вам дали рівносторонній трикутник, в якому всі сторони вимірювали 4 дюйма? Як ви могли використовувати теорему Піфагора, щоб знайти висоту трикутника?
Яка висота рівнобедреного трикутника?
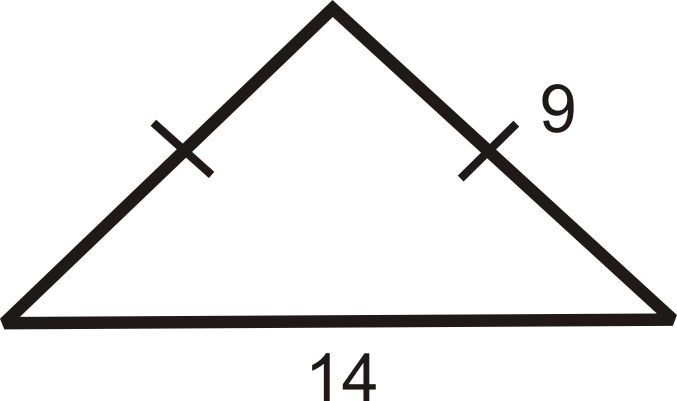
Рішення
Намалюйте висоту від вершини між конгруентними сторонами, яка буде розділяти основу.
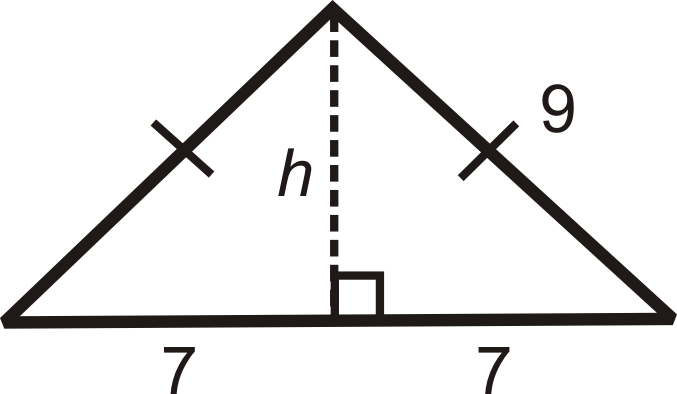
\(\begin{aligned} 7^2+h^2 &=9^2 \\ 49+h^2&=81 \\ h^2&=32 \\ h&=\sqrt{32}=\sqrt{16 \cdot 2}=4\sqrt{2}\end{aligned}\)
Знайти відстань між\((1, 5)\) і\((5, 2)\).
Рішення
Зробити\(A(1,5)\) і\(B(5,2)\). Підключіть до формули відстані.
\(\begin{aligned} d&=\sqrt{(1−5)^2+(5−2)^2} \\ &=\sqrt{(−4)^2+(3)^2}\\ &=\sqrt{16+9}=\sqrt{25}=5 \end{aligned} \)
Так само, як і довжини сторін трикутника, відстані завжди позитивні.
Графік\(A(−4,1)\),\(B(3,8)\), і\(C(9,6)\). Визначте, чи\(\Delta ABC\) є гострим, тупим, або правий.
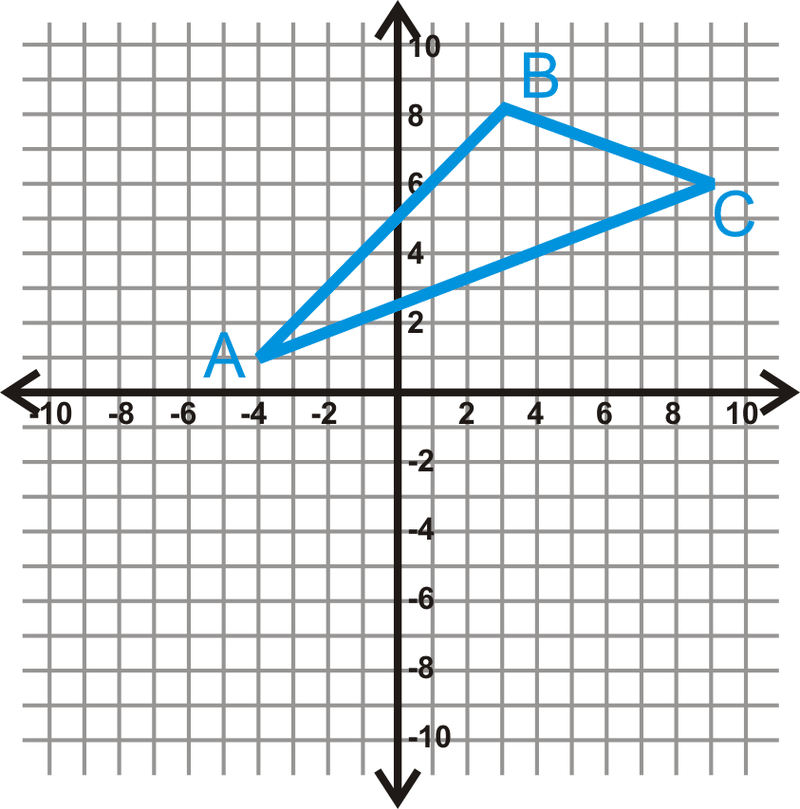
Рішення
Використовуйте формулу відстані, щоб знайти довжину кожної сторони.
\(\begin{aligned} AB&=\sqrt{(−4−3)^2+(1−8)^2}=\sqrt{49+49}=\sqrt{98} \\ BC&=\sqrt{(3−9)^2+(8−6)^2}=\sqrt{36+4}=\sqrt{40} \\ AC&=\sqrt{(−4−9)^2+(1−6)^2}=\sqrt{169+25}=\sqrt{194}\end{aligned}\)
Підключіть ці довжини до теореми Піфагора.
\(\begin{aligned} (\sqrt{98})^2+(\sqrt{40})^2 &? (\sqrt{194})^2 \\ 98+40 &? 194\\ 138 &<194 \end{aligned}\)
\(\Delta ABC\)є тупим трикутником.
Для прикладів 4 і 5 визначте, чи трикутники є гострими, правильними або тупими.
Встановіть найдовшу сторону\(c\).
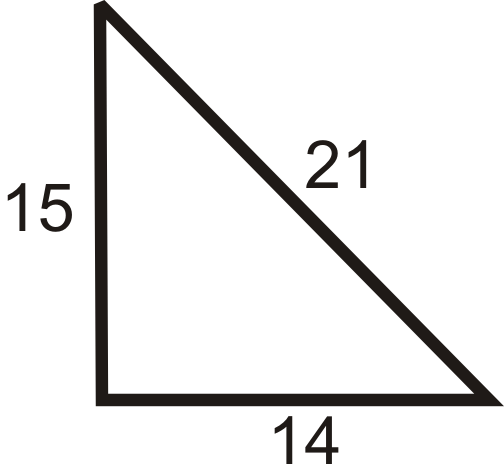
Рішення
\(\begin{aligned} 15^2+14^2 &? 21^2 \\ 225+196 &? 441 \\ 421 &<441\end{aligned}\)
Трикутник тупий.
Встановіть найдовшу сторону\(c\).
Трикутник з довжиною сторін 5, 12, 13.
Рішення
\(5^2+12^2=13^2\)так що цей трикутник є правильним.
Рецензія
Знайдіть висоту кожного рівнобедреного трикутника нижче. Спростити всі радикали.
-
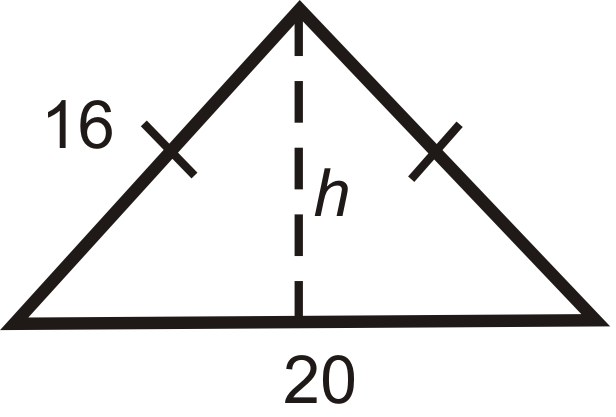
Малюнок\(\PageIndex{10}\) -
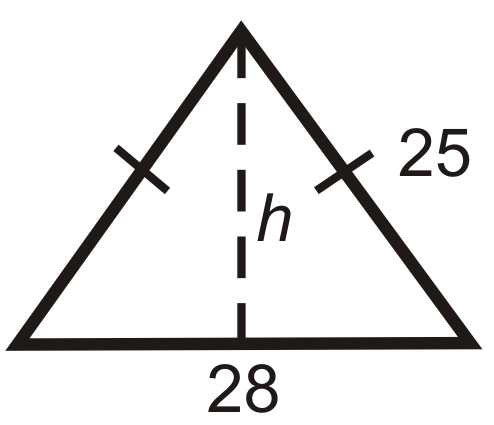
Малюнок\(\PageIndex{11}\) -
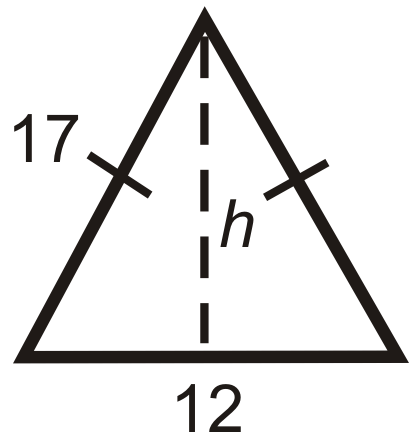
Малюнок\(\PageIndex{12}\)
Знайдіть довжину між кожною парою точок.
- (-1, 6) і (7, 2)
- (10, -3) і (-12, -6)
- (1, 3) і (-8, 16)
- Яка довжина і ширина 42-дюймового телевізора HDTV? Округлите відповідь до найближчої десятої.
- Телевізори стандартної чіткості мають співвідношення довжини і ширини 4:3. Яка довжина та ширина 42-дюймового телевізора стандартної чіткості? Округлите відповідь до найближчої десятої.
Визначте, чи є наступні трикутники гострими, правильними або тупими.
- 7, 8, 9
- 14, 48, 50
- 5, 12, 15
- 13, 84, 85
- 20, 20, 24
- 35, 40, 51
- 39, 80, 89
- 20, 21, 38
- 48, 55, 76
Графік кожної множини точок і визначити, чи\(\Delta ABC\) є гострим, правим або тупим, використовуючи формулу відстані.
- \(A(3,−5), B(−5,−8), C(−2,7)\)
- \(A(5,3),B(2,−7),C(−1,5)\)
- \(A(1,6),B(5,2),C(−2,3)\)
- \(A(−6,1),B(−4,−5),C(5,−2)\)
Огляд (Відповіді)
Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 8.3.