1.2: Конверс теореми Піфагора
- Page ID
- 54795
Визначте правильні трикутники за допомогою теореми
Вивести та використати зворотне теореми Піфагора

Брендон щойно придбав свій перший будинок і дуже прагне посадити квітник на трикутній ділянці заднього двору. Брендон успадкував металевий паркан, який його дід зробив багато років тому, і він хотів би використовувати його у своєму саду. Паркан складається з двох частин, які зварені між собою, щоб утворити прямий кут, і ще один довгий прямий шматок. Він знає, що шматки паркану впишуться в сад, якщо його трикутний сад - прямокутний трикутник.
«Якби я міг використовувати садові вимірювання 29 футів, 20 футів і 29 футів, щоб з'ясувати, чи утворює мій садовий простір прямокутний трикутник, то я міг би використовувати паркан дідуся». він подумав про себе.
У цьому понятті ви навчитеся виводити і використовувати зворотну теорему Піфагора.
Конверс теореми Піфагора
Теорема Піфагора стверджує, що для прямокутного трикутника квадрат довжини гіпотенузи дорівнює сумі квадратів довжин двох інших сторін. Ця теорема може бути змодельована рівнянням,\(c^2=a^2+b^2\) де\(c\) '' представляє довжину гіпотенузи, 'a' представляє довжину одного катета, а 'b' представляє довжину іншого катета.
Теорема Піфагора може бути використана для обчислення довжини невідомої сторони прямокутного трикутника. Конверс теореми Піфагора стверджує, що якщо квадрат довжини однієї сторони трикутника дорівнює сумі квадратів довжин двох інших сторін, то кут, протилежний найдовшій стороні, є прямим кутом. Трикутник, який містить прямий кут, - це прямокутний трикутник.
Давайте розглянемо зворотне теореми Піфагора в дії.
Визначте, чи є наступні трикутники (які не можуть бути намальовані в масштабі) є прямими трикутниками. Якщо трикутник являє собою прямокутний трикутник, внесіть будь-які необхідні зміни в трикутник і намалюйте його правильно.
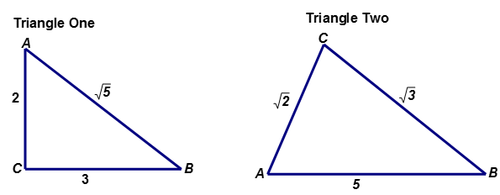
Почнемо з трикутника один.
Спочатку визначте найдовшу сторону трикутника.
Довжини сторін - 2, 3 і\(\sqrt{5}\). Довжина боку\(BC\) дорівнює\(\sqrt{5}\approx 2.24 \text{ units}\). Найдовша сторона трикутника,\(AB\) яка буде гіпотенузою трикутника, якщо\(\Delta ABC\) це прямокутний трикутник.
Далі підставляємо значення\((2,\sqrt{5},3)\)\((a,b,c) \) відповідно до рівняння c^2=a^2+b^2.
c^2&=a^2+b ^ 2\\ (3) ^2&= (2) ^2+ (\ sqrt {5}) ^2
Далі поставте квадрат кожного з членів, зазначених у рівнянні.
\(\begin{aligned} (3)^2&=(2)^2+(\sqrt{5})^2 \\ (3\times 3)&=(2 \times 2)+(\sqrt{5}\times \sqrt{5})\end{aligned}\)
Далі оцінюємо кожен з квадратів.
\(\begin{aligned} (3\times 3)&=(2\times 2)+(\sqrt{5} \times \sqrt{5}) \\ 9&=4+5 \end{aligned}\)
Потім спростіть праву частину рівняння, склавши числа.
\(\begin{aligned} 9&=4+5 \\ 9&=9 \end{aligned}\)
Обидві сторони рівняння рівні. Квадрат довжини однієї сторони трикутника дорівнює сумі квадратів довжин двох інших сторін. Трикутник Один - прямокутний трикутник. Довжина\(BC\) повинна бути 3, а довжина\(AB\) повинна бути,\(\sqrt{5}\) так як прямий кут розташований на\(C\).
Давайте подивимося на трикутник два.
Спочатку визначте найдовшу сторону трикутника.
Довжини сторін складають\(\sqrt{2}\),\(\sqrt{3}\) і 5. Довжина сторони\(AC\) становить\(\sqrt{2}\) приблизно 1,41 одиниці довжини. Довжина сторони BC становить\(\sqrt{3}\), приблизно 1,73 одиниці в довжину. Найдовша сторона трикутника - AB, яка буде гіпотенузою трикутника, якщо\(\Delta ABC\) це прямокутний трикутник.
Далі підставляємо значення\((\sqrt{2},\sqrt{3},5)\)\((a,b,c)\) відповідно в рівняння\(c^2=a^2+b^2\).
\ (\ почати {вирівняний} c^2&=a^2+b ^ 2\\ (5) 2&= (\ sqrt {2}) ^2+ (\ sqrt {3}) ^2\ кінець {вирівняний}、)
Далі поставте квадрат кожного з членів, зазначених у рівнянні.
\(\begin{aligned} (5)^2&=(\sqrt{2})^2+(\sqrt{3})^2 \\ (5\times 5)&=(\sqrt{2}\times \sqrt{2})+(\sqrt{3}\times \sqrt{3})\end{aligned}\)
Далі оцінюємо кожен з квадратів.
\(\begin{aligned} (5\times 5)&=(\sqrt{2}\times \sqrt{2})+(\sqrt{3}\times \sqrt{3}) \\ 25&=2+3 \end{aligned}\)
Потім спростіть праву частину рівняння, склавши числа.
\(\begin{aligned}25&=2+3 \\ 25&\neq 5\end{aligned}\)
Обидві сторони рівняння не рівні. Квадрат довжини однієї сторони трикутника НЕ дорівнює сумі квадратів довжин двох інших сторін. Трикутник Два - це не прямокутний трикутник.
Раніше вам давали проблему з приводу квітника Брендона і його металевого паркану. Йому потрібно розібратися, чи є його садовий простір прямокутним трикутником. Як Брендон може зрозуміти це за допомогою вимірювань простору?
Рішення
Спочатку визначте значення для (a, b, c) прямокутного трикутника за допомогою вимірювань 29, 20 і 21 футів.
Найдовша сторона буде представляти\(c\) гіпотенузу.
\(\begin{aligned} a&=20 \\ b&=21 \\ c&=29 \end{aligned}\)
Далі підставляємо задані значення в теорему Піфагора.
\(\begin{aligned} c^2=a^2+b^2 \\ (29)^2=(20)^2+(21)^2\end{aligned}\)
Далі поставте квадрат кожного з членів, зазначених у рівнянні.
\(\begin{aligned} (29)^2&=(20)^2+(21)^2 \\ (29\times 29)&=(20\times 20)+(21\times 21) \end{aligned}\)
Далі оцінюємо кожен з квадратів і спрощуємо рівняння.
\(\begin{aligned} (29\times 29)&=(20\times 20)+(21\times 21) \\ 841&=400+441 \\ 841&=841\end{aligned}\)
Квадрат довжини однієї сторони трикутника дорівнює сумі квадратів довжин двох інших сторін. Сад являє собою прямокутний трикутник.
Брендон може використовувати паркан свого дідуся для свого квітника.
Чи є множина чисел (5, 8, 10) довжинами сторін прямокутного трикутника?
Рішення
Спочатку визначте значення для кожної сторони прямокутного трикутника. Довжина найдовшої сторони буде представляти 'c, 'гіпотенузу. Інші дві довжини представлятимуть довжини ніг 'a' і 'b'.
\(\begin{aligned} a&=5 \\ b&=8 \\ c&=10 \end{aligned}\)
Далі підставляємо задані значення в теорему Піфагора.
\(\begin{aligned} c^2&=a^2+b^2 \\ (10)^2&=(5)^2+(8)^2 \end{aligned}\)
Далі поставте квадрат кожного з членів, зазначених у рівнянні.
\(\begin{aligned} (10)^2&=(5)^2+(8)^2 \\ (10\times 10)&=(5\times 5)+(8\times 8) \end{aligned}\)
Далі оцінюємо кожен з квадратів.
\(\begin{aligned} (10\times 10)&=(5\times 5)+(8\times 8) \\ 100&=25+64 \end{aligned}\)
Потім спростіть праву частину рівняння, склавши числа.
\(\begin{aligned} 100&=25+64 \\ 100&\neq 89\end{aligned}\)
Обидві сторони рівняння не рівні. Квадрат довжини однієї сторони трикутника НЕ дорівнює сумі квадратів довжин двох інших сторін.
Безліч чисел (5, 8, 10) - це не довжини сторін прямокутного трикутника.
Чи є наступний трикутник (який може бути намальований або не може бути намальований в масштабі) прямокутним трикутником?
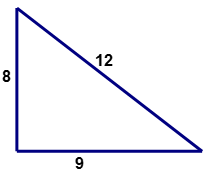
Рішення
Спочатку визначте значення для (a, b, c) прямокутного трикутника. Найдовша сторона буде представляти 'c' гіпотенузу.
\(\begin{aligned} a&=8 \\ b&=9 \\ c&=12 \end{aligned}\)
Далі підставляємо задані значення в теорему Піфагора.
\(\begin{aligned} c^2&=a^2+b^2 \\ (12)^2&=(8)^2+(9)^2 \end{aligned}\)
Далі поставте квадрат кожного з членів, зазначених у рівнянні.
\(\begin{aligned} (12)^2&=(8)^2+(9)^2 \\ (12\times 12)&=(8\times 8)+(9\times 9) \end{aligned}\)
Далі оцінюємо кожен з квадратів.
\(\begin{aligned} (12\times 12)&=(8\times 8)+(9\times 9) \\ 144&=64+81 \end{aligned}\)
Потім спростіть праву частину рівняння, склавши числа.
\(\begin{aligned}144&=64+81 \\ 144 &\neq 145\end{aligned} \)
Обидві сторони рівняння не рівні. Квадрат довжини однієї сторони трикутника НЕ дорівнює сумі квадратів довжин двох інших сторін. Трикутник - це не прямокутний трикутник.
Чи є наступний трикутник (який може бути намальований або не може бути намальований в масштабі) прямокутним трикутником?
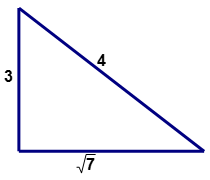
Рішення
Спочатку визначте значення для (a, b, c) прямокутного трикутника. Найдовша сторона буде представляти 'c' гіпотенузу.
\(\begin{aligned}\sqrt{7}&\approx 2.65\\ a&=3 \\ b&=\sqrt{7} \\ c&=4\end{aligned}\)
Далі підставляємо задані значення в теорему Піфагора.
\(\begin{aligned} c^2&=a^2+b^2 \\ (4)^2&=(3)^2+(\sqrt{7})^2 \end{aligned}\)
Далі поставте квадрат кожного з членів, зазначених у рівнянні.
\(\begin{aligned} (4)^2&=(3)^2+(\sqrt{7})^2 \\ (4\times 4)&=(3\times 3)+(\sqrt{7}\times \sqrt{7}) \end{aligned}\)
Далі оцінюємо кожен з квадратів.
\(\begin{aligned} (4\times 4)=(3\times 3)+(\sqrt{7}\times \sqrt{7}) \\ 16&=9+7\end{aligned}\)
Потім спростіть праву частину рівняння, склавши числа.
\(\begin{aligned} 16&=9+7 \\ 16&=16 \end{aligned}\)
Обидві сторони рівняння рівні. Квадрат довжини однієї сторони трикутника дорівнює сумі квадратів довжин двох інших сторін. Трикутник - прямокутний трикутник.
Рецензія
Подумайте про те, що ви дізналися про теорему Піфагора, і дайте відповідь істинно чи помилково на наступні питання.
1. Теорема Піфагора працюватиме для гострого трикутника з усіма кутами 60°.
2. Теорема Піфагора буде працювати для прямокутного трикутника.
3. Теорема Піфагора буде працювати тільки в тому випадку, якщо трикутник є прямокутним трикутником.
4. Ніжки прямокутного трикутника вважаються двома коротшими сторонами прямокутного трикутника.
5. Гіпотенуза - найдовша сторона прямокутного трикутника.
6. Зворотна теорема Піфагора використовується для пошуку кутових мір тупого трикутника.
7. Піфагорійська трійка - це коли ви помножуєте всі кутові заходи на три.
8. Ви можете використовувати теорему Піфагора, щоб з'ясувати, чи довжини сторін трикутника роблять його прямокутним трикутником чи ні.
Визначте, чи є кожне з наступних значень Піфагорійською трійкою. Напишіть так чи ні для вашої відповіді.
9. (4, 5, 6)
10. (6, 8, 10)
11. (5, 6, 9)
12. (9, 12, 15)
13. (30, 40, 55)
14. (21, 28, 35)
15. (12, 16, 20).
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 7.7.
Ресурси
Додаткові ресурси
Відео: Теорема Піфагора та зворотне значення теореми Піфагора
Практика: Конверс теореми Піфагора