9.5 Гіперболи
- Page ID
- 54592
Гіперболи - це відносини, які мають асимптоти. При графіку раціональних функцій ви часто створюєте гіперболу. У цій концепції гіперболи не будуть орієнтовані так само, як з раціональними функціями, але основна форма гіперболи все одно буде.
Гіперболи можна орієнтувати так, щоб вони відкривалися з боку в бік або вгору-вниз. Однією з найпоширеніших помилок, яку ви можете зробити, є забути, яким шляхом повинна відкриватися дана гіпербола. Які стратегії допоможуть?
Графічні гіперболи
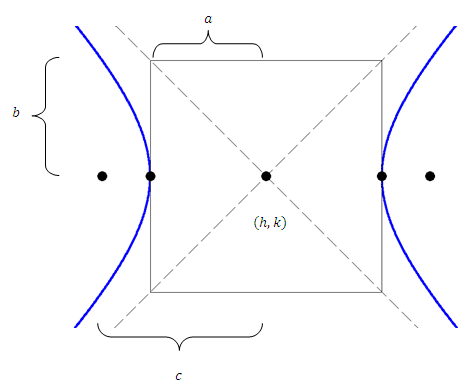
Гіпербола має два вогнища. Для кожної точки на гіперболі різниця відстаней до кожного вогнища постійна. Це те, що визначає гіперболу. Графічна форма гіперболи, яка відкривається з боку в бік, є:
\(\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1\)
Гіпербола, яка відкривається вгору і вниз, це:
\(\frac{(y-k)^{2}}{a^{2}}-\frac{(x-h)^{2}}{b^{2}}=1\)
Зверніть увагу, що для гіпербол,\(a\) йде з позитивним терміном і\(b\) йде з негативним терміном. Неважливо, яка константа більше.
При побудові графіків константи\(a\) і\(b\) дозволяють намалювати прямокутник навколо центру. Поперечна вісь рухається від вершини до вершини і має довжину\(2 a\). Сполучений вісь рухається перпендикулярно поперечній осі через центр і має довжину\(2 b\). Вогнища лежать за вершинами, тому ексцентриситет, який\(e=\frac{c}{a},\) вимірюється як більше 1 для всіх гіпербол. Гіперболи також мають дві прямі прямі, які знаходяться\(\frac{a^{2}}{c}\) далеко від центру (не показані на зображенні).
Фокусний радіус дорівнює\(a^{2}+b^{2}=c^{2}\)
Приклади
Раніше вас запитали, як визначити напрямок, яке відкриває гіпербола. Найкраща стратегія запам'ятати, в якому напрямку відкривається гіпербола, часто найпростіша. Розглянемо гіперболу\(x^{2}-y^{2}=1\). Ця гіпербола відкривається з боку в бік, тому що явно ніколи не\(x\) може дорівнювати нулю. Це основний випадок, який показує, що коли негатив зі\(y\) значенням, то гіпербола відкривається з боку в бік.
Помістіть наступну гіперболу в графічну форму, перерахуйте компоненти та намалюйте її.
\(9 x^{2}-4 y^{2}+36 x-8 y-4=0\)
\(\begin{aligned} 9\left(x^{2}+4 x\right)-4\left(y^{2}+2 y\right) &=4 \\ 9\left(x^{2}+4 x+4\right)-4\left(y^{2}+2 y+1\right) &=4+36-4 \\ 9(x+2)^{2}-4(y+1)^{2} &=36 \\ \frac{(x+2)^{2}}{4}-\frac{(y+1)^{2}}{9} &=1 \end{aligned}\)
Форма: Гіпербола, яка відкривається горизонтально.
Центр: (-2, -1)
\(a=2\)
\(b=3\)
\(c=\sqrt{13}\)
\(e=\frac{c}{a}=\frac{\sqrt{13}}{2}\)
\(d=\frac{a^{2}}{c}=\frac{4}{\sqrt{13}}\)
Вогнища:\(\left(-2+\frac{\sqrt{13}}{2},-1\right),\left(-2-\frac{\sqrt{13}}{2},-1\right)\)
Вершини: (-4, -1), (0, -1)
Рівняння асимптотів:\(\pm \frac{3}{2}(x+2)=(y+1)\)
Зауважте, що найпростіше записати рівняння асимптот у точково-схильній формі, використовуючи центр і нахил.
Рівняння директорів:\(y=-2 \pm \frac{4}{\sqrt{13}}\)
Знайдіть рівняння гіперболи з вогнищами при (-3,5) і (9,5) і асимптотах з нахилами\(\pm \frac{4}{3}\).
Центр знаходиться між вогнищами в (3,5). Фокусний радіус є\(c=6\). Нахил асимптотів - це завжди підйом над пробігом всередині коробки. У цьому випадку так як гіпербола горизонтальна і\(a\) знаходиться в\(x\) напрямку нахилу\(\frac{b}{a}\). Це робить систему рівнянь.
\(\frac{b}{a}=\pm \frac{4}{3}\)
\(a^{2}+b^{2}=6^{2}\)
Коли ви вирішуєте, ви отримуєте\(a=\sqrt{13}, b=\frac{4}{3} \sqrt{13}\).
\(\frac{(x-3)^{2}}{13}-\frac{(y-5)^{2}}{\frac{16}{9} \cdot 13}=1\)
Знайдіть рівняння конічного конуса, що має точку фокусування в (1,2), директрису в\(x=5\) і ексцентриситет рівний\(\frac{3}{2}\). Скористайтеся властивістю, що відстань від точки на гіперболі до фокусу дорівнює ексцентриситету на відстань від тієї ж точки до директриси:
\(\overline{P F}=e \overline{P D}\)
Цей зв'язок перемикає зазор між еліпсами, які мають ексцентриситет менше одиниці, і гіперболами, які мають ексцентриситет більше одиниці. Коли ексцентриситет дорівнює одиниці, то
форма - парабола.
\(\sqrt{(x-1)^{2}+(y-2)^{2}}=\frac{3}{2} \sqrt{(x-5)^{2}}\)
Квадратуйте обидві сторони і переставляйте терміни так, щоб він став гіперболою у графічній формі.
\(\begin{aligned} x^{2}-2 x+1+(y-2)^{2} &=\frac{9}{4}\left(x^{2}-10 x+25\right) \\ x^{2}-2 x+1-\frac{9}{4} x^{2}+\frac{90}{4} x-\frac{225}{4}+(y-2)^{2} &=0\\-\frac{5}{4} x^{2}+\frac{92}{4} x+(y-2)^{2} &=\frac{221}{4}\\-5 x^{2}+92 x+4(y-2)^{2} &=221\\-5\left(x^{2}-\frac{92}{5} x\right)+4(y-2)^{2} &=221 \end{aligned}\)
\(\begin{aligned}-5\left(x^{2}-\frac{92}{5} x+\frac{92^{2}}{10^{2}}\right)+4(y-2)^{2} &=221-\frac{2116}{5}\\-5\left(x-\frac{92}{10}\right)^{2}+4(y-2)^{2} &=-\frac{1011}{5} \\\left(x-\frac{92}{10}\right)^{2}-(y-2)^{2} &=\frac{1011}{100} \\ \frac{\left(x-\frac{92}{10}\right)^{2}}{\left(\frac{1011}{100}\right)}-\frac{(y-2)^{2}}{\left(\frac{1011}{100}\right)} &=1 \end{aligned}\)
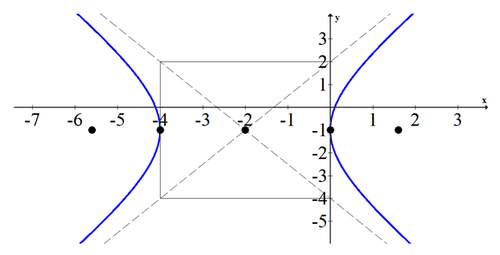
З огляду на наступний графік, оцініть рівняння конічного конуса.
Оскільки точні точки не позначені, вам потрібно буде оцінити нахил асимптотів, щоб отримати наближення для\(a\) і\(b\). Схил начебто приблизно\(\pm \frac{2}{3}\). Центр начебто знаходиться на\((-1\), -2). Поперечна вісь дорівнює 6, що означає\(a=3\).
\(\frac{(x+1)^{2}}{9}-\frac{(y+2)^{2}}{4}=1\)
Використовуйте наступне рівняння для #1 - #5:\(x^{2}+2 x-4 y^{2}-24 y-51=0\)
1. Помістіть гіперболу в графічну форму. Поясніть, як ви знаєте, що це гіпербола.
2. Визначте, чи відкривається гіпербола з боку в бік або вгору-вниз.
3. Знайдіть розташування вершин.
4. Знайдіть рівняння асимптотів.
5. Намалюйте гіперболу.
Використовуйте наступне рівняння для\(\# 6-\# 10:-9 x^{2}-36 x+16 y^{2}-32 y-164=0\)
6. Помістіть гіперболу в графічну форму. Поясніть, як ви знаєте, що це гіпербола.
7. Визначте, чи відкривається гіпербола з боку в бік або вгору-вниз.
8. Знайдіть розташування вершин.
9. Знайдіть рівняння асимптотів.
10. Намалюйте гіперболу.
Використовуйте наступне рівняння для #11 - #15:\(x^{2}-6 x-9 y^{2}-54 y-81=0\)
11. Помістіть гіперболу в графічну форму. Поясніть, як ви знаєте, що це гіпербола.
12. Визначте, чи відкривається гіпербола з боку в бік або вгору-вниз.
13. Знайдіть розташування вершин.
14. Знайдіть рівняння асимптотів.
15. Намалюйте гіперболу.