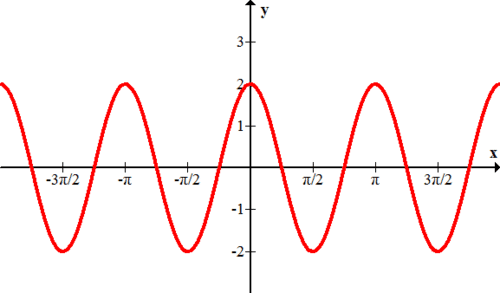
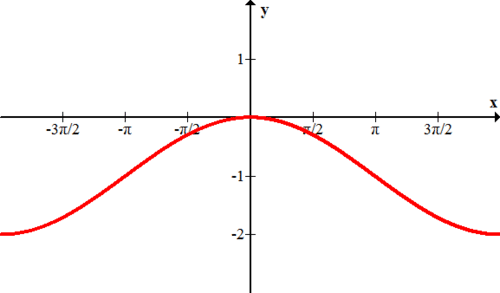
5.5: Частота і період синусоїдальних функцій

Правила перетворення щодо горизонтального розтягування та скорочення безпосередньо застосовуються до синусоїдних та косинусних графіків. Якщо синусоїдальний графік розтягується по горизонталі на коефіцієнт\(\frac{1}{2}\), це те саме, що і горизонтальне стиснення на коефіцієнт 2.

Як змінюється рівняння, коли граф синуса або косинуса розтягується в 3 рази?

Період і частота синусоїдальних функцій

Загальне рівняння для синусоїдальної функції таке:

f (x) = ± a⋅син (b (x+c)) +д

\(\pm\)Керує відображенням поперек\(x\) -осі. Коефіцієнт\(a\) контролює амплітуду. Постійна\(d\) контролює вертикальний зсув. Тут ви побачите, що коефіцієнт\(b\) керує горизонтальним розтягуванням.

Період

Горизонтальна розтяжка вимірюється для синусоїдальних функцій як їх періодів. Ось чому це сімейство функцій ще називають сімейством періодичних функцій. Період синусоїди - це довжина повного циклу. Для основних синусоїдних і косинусних функцій період дорівнює\(2 \pi\). Цю довжину можна виміряти різними способами. У проблемах зі словами та в інших складних обставин може бути найкориснішим виміряти від піку до піку.

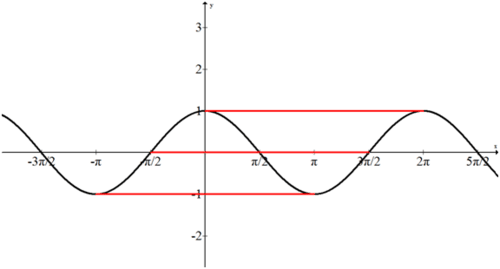
Наступні три хвилі мають різні періоди. Щоб ранжувати кожну хвилю за періодом від найкоротшої до найдовшої, подивіться на відстань між кожною вершиною.

Червона хвиля має найкоротший період.

Зелена і чорна хвилі мають рівні періоди. Незважаючи на те, що зелена хвиля має більшу амплітуду, ніж чорна хвиля, вони обидва мають однаковий період.

Блакитна хвиля має найдовший період.

Можливість вимірювати період функції кількома способами дозволяє різним рівнянням моделювати однаковий графік. На зображенні вище верхня червона лінія представляла б регулярну хвилю косинуса. Центральна червона лінія представляла б собою регулярну синусоїду з горизонтальним зсувом. Нижня червона лінія представляла б негативну косинусну хвилю з горизонтальним зсувом. Ця гнучкість у перспективі означає, що багато прикладів, керованої практики та проблем практики можуть мати кілька рішень. Наразі намагайтеся завжди вибирати функцію, яка має період, починаючи з\(x=0\).

Частота

Частота - це інший спосіб вимірювання горизонтальної розтяжки. Для звуку частота відома як висота тону. При синусоїдальних функціях частота - це кількість циклів, які відбуваються в\(2 \pi\). Більш короткий період означає, що більше циклів може вміститися\(2 \pi\) і, таким чином, більш висока частота. Період і частота обернено пов'язані рівнянням:

період\(=\frac{2 \pi}{\text { frequency }}\)

Рівняння основної синусоїдальної функції є\(f(x)=\sin x\). У цьому випадку частота\(b\), дорівнює 1, що означає, що один цикл відбувається в\(2 \pi .\) Якщо\(b=\frac{1}{2},\) період є,\(\frac{2 \pi}{\frac{1}{2}}\) що означає, що період є\(4 \pi\) і графік розтягується.

Приклади

Приклад 1

Раніше вас запитали, як змінюється рівняння, коли графік синуса або косинуса розтягується в 3 рази. Якщо синусоїдальний графік горизонтально розтягується на коефіцієнт 3, то загальне рівняння має\(b=\frac{1}{3}\). Це пов'язано з тим\(b\), що частота і підраховує кількість (або дріб) періоду, який вписується в нормальний період\(2 \pi\). Графічно синусоїда зробить повний цикл в\(6 \pi\). Аналогічно, косинус граф буде мати\(b=\frac{1}{3}\) і буде мати період\(6 \pi\).

Приклад 2

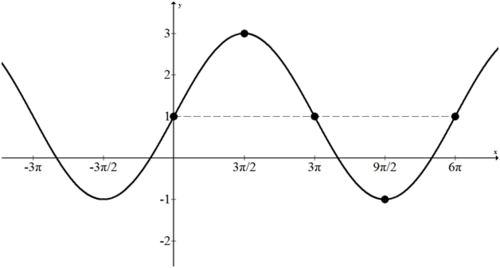
Визначте амплітуду, вертикальний зсув, період і частоту наступної функції. Потім графік функції.

\(f(x)=2 \sin \left(\frac{x}{3}\right)+1\)

\(a=2, b=\frac{1}{3}, d=1\)

Амплітуда - 2, вертикальний зсув -\(1,\) і частота -\(\frac{1}{3}\). Період був би\(\frac{2 \pi}{\frac{1}{3}}\), або\(6\pi\).

Часто найскладнішою частиною графічних періодичних функцій є маркування осей. Оскільки період\(6 \pi,\) починається з малювання синусоїдальної осі, зміщеної відповідним чином. Потім розділіть їх\(6 \pi\) на чотири частини так, щоб 5 напрямних точок синусоїдального графіка можна було побудувати з урахуванням амплітуди та відображення. Найостанніше, що потрібно зробити, це намалювати і подовжити криву.

Приклад 3

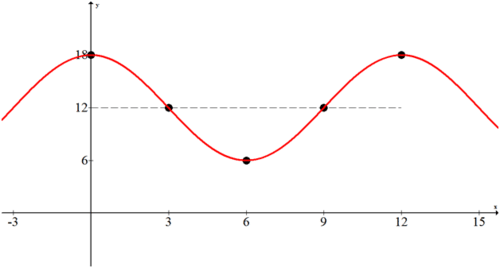
Вимірювальна палиця на доці вимірює приплив, щоб бути 18 футів, а відлив - 6 футів. Для перемикання між відливами і припливами потрібно близько 6 годин. Визначте графічну та алгебраїчну модель для припливів, знаючи, що при цьому\(t=0\) відбувається приплив.

Зазвичай найкращим способом дій для проблем зі словами є виявлення інформації, сюжетних точок, ескізу, а потім, нарешті, придумати рівняння.

З наданої інформації можна вивести наступні моменти. Зверніть увагу, як синусоїдальну вісь можна вважати середнім показником високих і відливів.

\ (
\ begin {масив} {|l|l|}
\ hline\ текст {Час (години)} &\ текст {Рівень води (фути)}
\\ hline 0 & 18
\\\ hline 6\\
\ hline 12 & 18\\
\ hline 3 &\\ frac {18+6} {2} =12\
\ hline 9 & 12 \\
\ hline
\ end {масив}
\)

Побудувавши ці точки та заповнивши синусоїдальну вісь, ви можете спостерігати графік косинусів.

Амплітуда - 6 так\(a=6\). Відсутнє вертикальне відображення. так як період 12 можна визначити частоту\(b\):

\(12=\frac{2 \pi}{b} \rightarrow b=\frac{\pi}{6}\)

Вертикальний зсув дорівнює 12 так\(d=12\). Таким чином, у вас є всі частини, щоб зробити алгебраїчну модель:

\(f(x)=6 \cdot \cos \left(\frac{\pi}{6} x\right)+12\)

Приклад 4

Графік наступної функції:\(g(x)=-\cos (8 x)+2\)

Маркування є найважливішою та складною частиною цієї проблеми. Амплітуда\(1 .\) Форма - негативний косинус. Вертикальний\(2 .\) зсув - це період\(\frac{2 \pi}{8}=\frac{\pi}{4}\)

Приклад 5

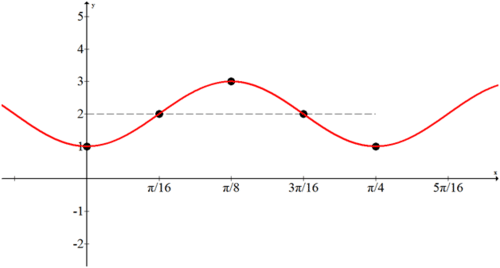
Враховуючи наступний графік, визначте амплітуду, період та частоту та створіть алгебраїчну модель.

Амплітуда\(3 .\) Форма - негативний косинус. Період - це те\(\frac{5 \pi}{2}\), що означає\(b=\frac{4}{5}\). Вертикальний зсув дорівнює 1. \(f(x)=-3 \cdot \cos \left(\frac{4}{5} x\right)+1\)

Рецензія

Нижче наведено частоту та період кожної функції.

1. \(f(x)=\sin (4 x)+1\)

2. \(g(x)=-3 \cos (2 x)\)

3. \(h(x)=\cos \left(\frac{1}{2} x\right)+2\)

4. \(k(x)=-2 \sin \left(\frac{3}{4} x\right)+1\)

5. \(j(x)=4 \cos (3 x)-1\)

Графік кожної з наступних функцій.

6. \(f(x)=3 \sin (2 x)+1\)

7. \(g(x)=2.5 \cos (\pi x)-4\)

8. \(h(x)=-\sin (4 x)-3\)

9. \(k(x)=\frac{1}{2} \cos (2 x)\)

10. \(j(x)=-2 \sin \left(\frac{3}{4} x\right)-1\)

Створіть алгебраїчну модель для кожного з наступних графіків.

11.

12.

13.

14. Під час 0 це приплив, а вода в певному місці висотою 10 футів. Під час відливу через 6 годин вода висотою 2 фути. Враховуючи, що припливи можна моделювати синусоїдальними функціями, знайдіть графік, який моделює цей сценарій.

15. Знайдіть рівняння, яке моделює сценарій у попередній задачі.

...