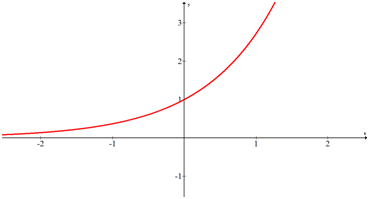
3.1: Експоненціальні функції
- Page ID
- 54449
Експоненціальне зростання - одна з найпотужніших сил в природі. Відома легенда свідчить, що винахідника шахів попросили викласти власну нагороду від короля. Чоловік попросив одне зерно рису для першого квадрата шахової дошки, два зерна рису для другого квадрата і чотири зерна рису для третього. Він попросив заповнити таким чином цілі 64 квадрати, і це було б його нагородою. Чоловік просив занадто мало, або занадто багато?
Експоненціальні функції
Експоненціальні функції набувають вигляду\(f(x)=a \cdot b^{x}\) де\(a\) і\(b\) є константами. \(a\)це стартова сума, коли\(x=0 . b\) розповідає історію про зростання. Якщо зростання подвоюється, то\(b\) дорівнює 2. Якщо зростання зменшується вдвічі (що було б розпадом), то\(b\) є\(\frac{1}{2}\). Якщо зростання збільшується на\(6 \%\)\(b\) тоді 1,06
Експоненціальне зростання є скрізь. Гроші ростуть в геометричній прогресії в банках. Популяції людей, бактерій та тварин зростають експоненціально, коли їх їжа та простір не обмежені.
Радіоактивні ізотопи, такі як Carbon 14, мають щось, що називається період напіврозпаду, який вказує, скільки часу потрібно для половини присутніх молекул розпаду на інші більш стабільні молекули. Це займає близько 5,730 років, щоб цей процес відбувся, як вчені можуть дати артефакти древніх людей.
Припустимо, муміфіковане тварина зустрічається збереженим на схилах крижаної гори. Після тестування ви бачите, що рівно одна четверта частина вуглецю-14 ще не розпалася, і ви хочете дізнатися, як давно була ця тварина жива. Як би ти це зробив?
Оскільки ця проблема не дає конкретних кількостей вуглецю, можна зробити висновок, що час не буде залежати від конкретних кількостей. Однією з методів, яка полегшує роботу з проблемою, може бути створення прикладу сценарію, який відповідає пропорції однієї четвертої. Припустимо, 60 одиниць були присутні, коли тварина була жива в той час нуль. Це означає, що сьогодні повинні бути присутніми 15 одиниць.
\(15=a \cdot\left(\frac{1}{2}\right)^{x}\)
\(60=a \cdot\left(\frac{1}{2}\right)^{0}\)
Друге рівняння дає,\(a=60\) а потім перше рівняння стає:
\(15=60 \cdot\left(\frac{1}{2}\right)^{x}\)
Хоча ви, можливо, ще не маєте алгебраїчних інструментів для вирішення\(x\), ви все одно повинні бути в змозі побачити, що\(x\) це\(2 .\) це не означає, що два роки тому тварина була жива, це означає, що два циклу напіврозпаду тому тварина була жива. Період напіввиведення вуглецю 14 становить 5730 років, тому ця тварина була жива понад 11 000 років тому.
Тепер, припустимо, ви вклали 100 доларів у день народження, і він зростав на 6% щороку, поки вам не виповнилося 100 років. Як би ви використали експоненціальну функцію, щоб визначити, скільки коштуватиме ця інвестиція?
Початкова сума становить 100, а зростання - 1,06, оскільки вона зростає\(6 \%\) з кожним роком. Цього достатньо інформації, щоб написати експоненціальну функцію. \(x\)Стенди для часу в роках і\(f(x)\) стенди для суми грошей на рахунку. Підключившись до формули для експоненціальної функції, ви отримаєте рівняння:
\(f(x)=100 \cdot 1.06^{x}\)
Потім, потрібно підставити через 100 років на\(x\).
\(f(x)=100 \cdot 1.06^{x}\)
\(f(x)=100 \cdot 1.06^{100}\)
\(f(x) \approx 33,930.21\)
Через століття на рахунку буде майже 34 000 доларів. Відсотки значно збільшили початкові інвестиції в розмірі 100 доларів.
Приклади
Раніше вас запитали, чи просив чоловік занадто мало або занадто багато рису, якщо він отримує одне зерно за перший квадрат, два зерна для другого, чотири зерна для третього і так далі. Кількість зерен рису на останньому квадраті, 64-му квадраті, становило б майже десять квінтильйонів (мільйонів мільйонів мільйонів). Тобто більше рису, ніж виробляється в світі за цілий рік.
\(2^{63}=9,223,372,036,854,775,808\)
Припустимо, сорок кроликів випускають на острів. Кролики спаровуються раз на чотири місяці і дають до 4 потомства, які також дають більше потомства через чотири місяці. Оцініть кількість кроликів на острові за 3 роки, якщо їх популяція зростає в геометричній прогресії. Припустимо, половина населення - жіноча.
Незважаючи на те, що частини цієї проблеми нереальні, вона служить для ілюстрації того, як швидко працює експоненціальне зростання. Сорок - початкова сума так\(a=40\). Наприкінці першого 4-місячного періоду 20 самок кроликів могли мати свої посліди та народитися до 80 новонароджених кроликів. Чисельність населення зросла з 40 до 120, що означає втричі. Таким чином,\(b=3\). Останнє, що потрібно пам'ятати, це те, що часовий період - це 4 місячні періоди. Три роки повинні бути 9 періодів.
\(f(x)=40 \cdot 3^{9}=787,320\)
Тож через три роки може бути до 787 320 кроликів!
Повністю проаналізуйте наступну експоненціальну функцію.
\(f(x)=e^{x}\)
Аналізувати в цьому контексті означає визначити всі характеристики функції.
Домен:\(x \in(-\infty, \infty)\)
Діапазон:\(y \in(0, \infty)\)
Збільшення:\(x \in(-\infty, \infty)\)
Зниження: NA
Нулі: Немає
Перехоплення: (0,1)
Максимуми: Немає
Мінімуми: Немає
Асимптоти:\(y=0\) як\(x\) стає нескінченно малим (горизонтальна асимптота)
Отвори: Немає
Визначте, які з наступних функцій є експоненціальними функціями, а які ні.
1. \(y=x^{6}\)
2. \(y=5^{x}\)
3. \(y=1^{x}\)
4. \(y=x^{x}\)
5. \(y=x^{\frac{1}{2}}\)
Експоненціальні функції мають вигляд\(y=a \cdot b^{x}\)
a. не\(y=x^{6}\) є експоненціальною функцією, оскільки не\(x\) знаходиться в експоненті.
б.\(y=5^{x}\) експоненціальна функція.
c\(y=1^{x}\) Не є істинною експоненціальною функцією, оскільки завжди\(y\) є 1, яка є постійною функцією.
d\(y=x^{x}\) Не є експоненціальною функцією, оскільки\(x\) є і базою, і силою показника.
е.\(y=x^{\frac{1}{2}}\) не експоненціальна функція.
Запишіть експоненціальну функцію, яка проходить через наступні точки:\((0,3),\left(1, \frac{3}{e}\right)\)
Стартовий номер -\(a=3\). Це число змінюється коефіцієнтом, від\(\frac{1}{e}\) якого є\(b\).
\(f(x)=3\left(\frac{1}{e}\right)^{x}=3 e^{-x}\)
Рецензія
1. Поясніть, що робить функцію експоненціальною функцією. Як виглядає його рівняння?
2. Чи є домен для всіх експоненціальних функцій дійсними числами?
3. Як ви можете визначити з його рівняння, чи буде збільшуватися графік експоненціальної функції?
4. Як ви можете визначити з його рівняння, чи буде граф експоненціальної функції зменшуватися?
5. Який тип асимптотів мають експоненціальні функції? Поясніть.
6. Припустимо, ви інвестували 4500 доларів, і вона росла на 4% щороку протягом 30 років. Скільки коштуватиме ця інвестиція через 30 років?
7. Припустимо, ви інвестували 10 000 доларів, і вона росла на 12% щороку протягом 40 років. Скільки коштувала б ця інвестиція через 40 років?
Запишіть експоненціальну функцію, яка проходить через наступні точки.
8. (0, 5) і (1, 25)
9. (0, 2) і (1, 8)
10. (0, 16) і (2, 144)
11. (1, 4) і (3, 36)
12. (0, 16) і (3, 2)
13. (0, 81) і (2, 9)
14. (1, 144) і (3, 12)
15. Поясніть, чому для експоненціальних функцій\(y=a \cdot b^{x}\) виду\(y\) -intercept завжди є значенням
\(a\)