8.1: Абсолютна крайність і оптимізація

Last updated
Save as PDF

Page ID: 54377

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

На цьому етапі ви знаєте, як проаналізувати функцію, щоб знайти її мінімуми та максимуми за допомогою першої та другої похідних. Пошук рішення якоїсь реальної проблеми (наприклад, у фінансах, науці та техніці) часто передбачає процес знаходження максимуму або мінімуму функції в межах прийнятного регіону значень. Такого роду завдання є задачею оптимізації, і рішення, яке є максимальним або мінімальним значенням функції в регіоні, є оптимальним рішенням. Налаштування проблеми оптимізації є важливим першим кроком. Подивіться, чи зможете ви встановити (але не вирішити) цю проблему: Які розміри зведуть до мінімуму кількість металу, необхідного для побудови накопичувального бака об'ємом 1000 м3, який має форму правого круглого циліндра і має верх, який є півсферою?

Оптимізація

У попередніх концепціях розглядалися методи знаходження максимумів і мінімумів (екстремумів) функцій, і ці методи використовуються при розв'язанні задач оптимізації. Припустимо, що f є безперервним на замкнутому інтервалі [a, b]. Нагадаємо, що ми можемо знайти абсолютний мінімум і максимум функції f, яка є безперервною на замкнутому інтервалі [a, b] наступним чином:

Знайти значення f для кожного критичного значення в (a, b);
Знайти значення функції f в кінцевих точках [a, b];
Абсолютним максимумом буде найбільше значення чисел, знайдених в 1 і 2; абсолютним мінімумом буде найменше число.

Однак реальні проблеми часто накладають обмеження, які необхідно враховувати при пошуку оптимального рішення.

Візьміть компанію, яка виготовляє високоякісні велосипедні шини як для рекреаційних, так і для гоночних гонщиків. Кількість шин, які компанія продає, є функцією ціни стягується і може бути змодельована за формулою$ T(x)=−x^3+36.5x^2+50x+250 \nonumber$, де x - ціна, що стягується за кожну шину в доларах. За якою ціною максимальна кількість проданих шин? Скільки шин буде продано за такою максимальною ціною?

У цій задачі оптимізації ми намагаємося знайти максимальне значення T (x). T (x) - первинне рівняння, яке буде оптимізовано. Давайте спочатку розглянемо графік функції шини і зробимо деякі спостереження. Встановіть діапазони вікон перегляду на графічному калькуляторі на [-10, 50] для x та [-500, 10000] для y.

Графік повинен виглядати наступним чином:

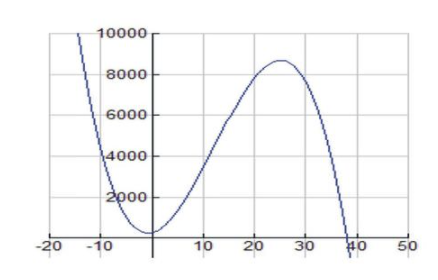
Знімок екрана 2021-01-04 в 2.24.13 PM.png

CC ЗА NC-SA

Спочатку зауважимо, що оскільки це реальне застосування, обидві величини, x і T (x), є позитивними, інакше проблема не має сенсу. Ці умови разом з тим, що нуль T (x) знаходиться на рівні x=37,9, дозволяють припустити, що фактична область цієї функції дорівнює 0<x≤37,9. Цей обмежений домен, який ми називаємо можливим доменом, ілюструє загальну рису задач оптимізації: реальні умови досліджуваної ситуації диктують значення домену.

Ми можемо скористатися графіком калькулятора або скористатися тестами Першого та Другого похідних, щоб знайти абсолютні максимуми та мінімуми на замкнутому інтервалі [0, 37,9].

^1-й похідний

\[ f′(x)=−3x^2+73x+50 \nonumber\]

f′ (х) =0:

в$x=− \frac{2}{3} \nonumber$... не в домені;

на x=25... у домені.

^2-а похідна

\[ f′′(x)=−6x+73 \nonumber\]

f′′ (25) =23

Існує функція максимум при x=25.

Ми бачимо, що функція досягає абсолютного максимуму при x = 25 в точці (25, 8687.5). Отже, стягнення ціни в 25 доларів призведе до продажу в цілому 8687 шин.

У багатьох задачах оптимізації вторинне рівняння (або більше одного) має використовуватися для зменшення кількості змінних у первинному рівнянні перед початком процедури оптимізації (використання графічного калькулятора; застосування похідних тестів).

Припустимо, що Мері бажає зробити відкриту прямокутну ручку для свого вихованця чихуахуа. Вона хотіла б, щоб перо облаштувати область на її задньому дворі з однією зі сторін прямокутника, зробленого стороною будинку Марії, як зазначено на наступному малюнку. Якщо у неї є 90 футів огорожі для роботи, які розміри пера призведуть до максимальної площі?

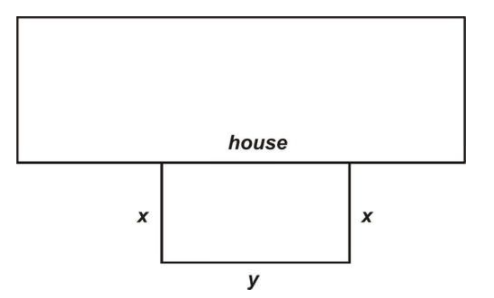
Знімок екрана 2021-01-04 в 2.26.41 PM.png

CC ЗА NC-SA

Розміри пера - х і у на малюнку. Первинне рівняння - це функція, яка моделює площу, А, пера. Бажаємо максимально:

\[ A=xy \nonumber\]

Вторинне рівняння походить від інформації, що стосується фехтування Мері повинна працювати с. Зокрема,

\[ 2x+y=90 \nonumber\]

Рішення для y у нас є

\[ y=90−2x \nonumber\]

Тепер підставляємо в первинне рівняння, щоб отримати:

$ A=xy=x(90−2x) \nonumber$, або

$ A(x)=−2x^2+90x \nonumber$

Завжди корисно переглянути графік функції, яку потрібно оптимізувати. Встановіть діапазони вікон перегляду на графічному калькуляторі на [-10, 100] для x та [-500, 1200] для y. Графік має виглядати наступним чином:

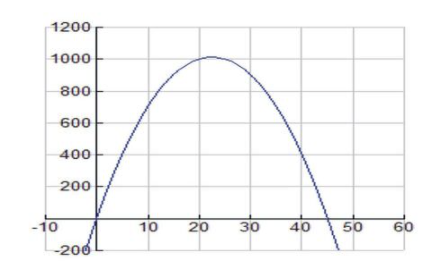
Знімок екрана 2021-01-04 в 2.34.06 PM.png

CC ЗА NC-SA

Допустима область цієї функції - 0<x<45, що має сенс, оскільки якщо x дорівнює 45 футів, то цифра буде двома огорожами довжиною 45 футів, що йдуть від будинку з 0 футами, залишеними на ширину y.

Розв'язок можна знайти за допомогою графічного калькулятора та/або першого та другого похідних тестів та методу знаходження абсолютних максимумів та мінімумів на замкнутому інтервалі (у цій задачі [0, 45]).

^1-й похідний

А′ (х) =−4x+90

A′ (х) =0:

на x=22.5... у домені.

^2-а похідна

A′′=−4

Існує функція максимум при x=22.5.

Ми бачимо, що функція досягає абсолютного максимуму в x=22,5 в точці (22,5, 1012,5).

Отже, розміри пера повинні бути x = 22,5, і y = 45; при цих розмірах перо буде охоплювати область 1012,5 футів 2.

Проблеми оптимізації за участю геометричних фігур дійсно допомагають проілюструвати процес розв'язання проблеми. Ось ще:

Певна марка лимонаду продає свій продукт у 16-унційних алюмінієвих банках, які вміщують 473 мл (1 мл = 1 см3). Знайдіть розміри циліндричної банки, яка буде використовувати найменшу кількість алюмінію.

Потрібно розробити формулу площі поверхні банки. Це складається з верхньої та нижньої областей$ πr^2 \nonumber$, кожна, і площі поверхні сторони,$ 2πrh \nonumber$ (твір окружності верхньої та висоти банки). Звідси первинне рівняння

\[ A=2πr^2+2πrh \nonumber\].

Ми спостерігаємо, що обидва наші можливі домени вимагають$r,h>0 \nonumber$.

Щоб зменшити кількість змінних в первинному рівнянні, нам знадобиться вторинне рівняння, яке дасть нам співвідношення між r і h. відзначимо, що обсяг для кругового циліндра задається тим$ V=πr^2h \nonumber$, що забезпечує зв'язок між r і h. Вторинне рівняння таке:

\[ h= \frac{V}{πr^2}= \frac{473}{πr^2} \nonumber\]

Підставляємо цей вираз для h в первинне рівняння, щоб отримати:

$ A(r)=2πr^2+2πr( \frac{473}{πr^2}) \nonumber$, або

\[ A(r)=2πr^2+\frac{946}{r} \nonumber\].

Графік функції A (r) показаний нижче:

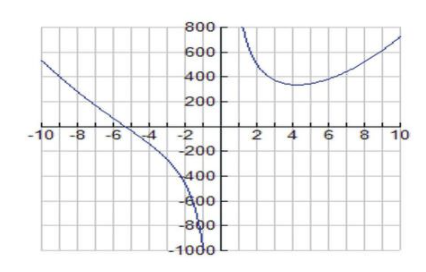
Знімок екрана 2021-01-05 о 12.19.50 PM.png

CC ЗА NC-SA

Допустимим доменом є r> 0.

^1-й похідний

\[ A′(r)=4πr− \frac{946}{r^2} \nonumber\]

A′ (r) =0:

на$ r= \frac{946}{4π}^{\frac{1}{3}}≈4.22 \nonumber$ см... в домені.

^2-а похідна

$ A′′(r)=4π+ \frac{1892}{r^3} \nonumber$

A′′ (r) > 0 для r>0

Існує функція мінімум r≈4,22 см.

Отже, ми маємо мінімальну площу поверхні 996,2 см2, коли r≈9,06 см і h≈8,44 см.

Приклади

Приклад 1

Раніше вас запитали про те, які розміри дозволять мінімізувати кількість металу, необхідного для побудови накопичувального бака об'ємом 1000 м3, який має форму правого круглого циліндра і має верх, який є півсферу.

Обсяг бака складається з обсягу циліндра і обсягу півсфери. Обсяг може бути виражений так:$ V=πr^2h+ \frac{1}{2}( \frac{4}{3}πr^3)=1000 \nonumber$ де r - радіус бака (в метрах), а h - висота циліндра (в метрах).

Ви хотіли б мінімізувати кількість використовуваного металу, що те саме, що просити мінімізувати площу бака. Це має бути постановка задачі оптимізації.

Площа може виражатися у вигляді:$ A=2πrh+ \frac{1}{2}(4πr^2) \nonumber$. Оскільки є дві змінні, r і h, ми повинні зробити h функцією r, тобто h (r), використовуючи рівняння для V.

\ [h (r) =\ frac {1000} {πr^2} −\ frac {2} {3} r\ nonumber\)

Постановка задачі оптимізації полягає в наступному:

$ \frac{dA}{dr}=0= \frac{d}{dr}[2πrh(r)+ \frac{1}{2}(4πr^2)]=2π[h(r)+r \frac{dh}{dr}+2r] \nonumber$, або

\[ h(r)+r \frac{dh}{dr}+2r=0 \nonumber\].

Наступним кроком є вирішення проблеми оптимізації, щоб побачити, чи є рішення, яке має сенс. Ви можете це зробити?

Приклад 2

Контейнер для зберігання повинен бути побудований з прямокутною основою, прямокутними сторонами та відкритим вгорі. Його ширина становить 4 метри, а обсяг - 36 кубічних метрів. Якщо будівництво бункера коштує 10 $/кв. м. за цоколь і 5 $/кв. м. для боків, то яка вартість найменш дорогого бункера? Які його розміри?

Нехай розміри бункера дорівнюють l довжині, ширині w і висоті h. Зверніть увагу, що w=4 метри.

Первинне рівняння - це функція, яка моделює вартість, C, бункера. Бажаємо мінімізувати:

\[ C=10lw+5[2lh+2wh]=10[lw+lh+wh]=10[4l+lh+wh] \nonumber\]

Вторинне рівняння виходить з інформації, що стосується обсягу бункера:

\[ V=lwh=4lh=36 \nonumber\]

Використання вторинного рівняння в первинному рівнянні:

\[ C=10[4l+lh+wh]=10[4l+\frac{36}{4}+\frac{36}{l}]=40[l+2.25+\frac{9}{l}] \nonumber\]

Розв'язок можна знайти за допомогою першого та другого похідних тестів та методу знаходження абсолютних максимумів та мінімумів на замкнутому інтервалі (у цій задачі [0, 45]).

^1-й похідний	\[ C′(l)=40(1−\frac{9}{l^2}) \nonumber\]	C′ (l) =0: при l=3 (у домені) та l = −3 (не у домені).
^2-а похідна	\[ C′′(l)=\frac{720}{l^3} \nonumber\]	КУ′ (3) ≈26.7. Функція витрат увігнута вгору. Існує функція мінімум при l=3.

^1-й похідний

\[ C′(l)=40(1−\frac{9}{l^2}) \nonumber\]

C′ (l) =0: при l=3 (у домені) та l = −3 (не у домені).

^2-а похідна

\[ C′′(l)=\frac{720}{l^3} \nonumber\]

КУ′ (3) ≈26.7. Функція витрат увігнута вгору.

Існує функція мінімум при l=3.

Отже, розміри бункера: l = 3 метри, w = 4 метри, і h = 3 метри.

Вартість побудови бункера: C (3) =40 $ (3+2.25+3) =330 $.

Рецензія

Для #1 -4 знайдіть абсолютні максимальні та абсолютні мінімальні значення, якщо вони існують.

$ f(x)=2x^2−6x+6 \mbox{ on } [0, 5] \nonumber$
$ f(x)=x^3+3x^2 \mbox{ on } [-2, 3] \nonumber$
$ f(x)=3x^{\frac{2}{3}}−6x+x \mbox{ on } [1, 8] \nonumber$
$ f(x)=x^4−x^3 \mbox{ on } [-2, 2] \nonumber$
Знайдіть розміри прямокутника, що має площу, периметр$ 2000 ft^2 \nonumber$ якого якомога менше.
Знайдіть два числа, добуток яких дорівнює 50 і сума яких мінімальна.
Джон стріляє в баскетбол з півкорту. Це приблизно 45 футів від лінії половини корту до обруча. Функція$ s(t)=−0.025x^2+x+15 \nonumber$ моделює висоту баскетболу над землею s (t) у футах, коли вона знаходиться t футів від обруча. У скільки футів від Джона м'яч досягне найвищої висоти? Що це за висота?
Висота моделі ракети t секунд у польоті задається за формулою$ h(t)=−13t^3+4t^2+25t+4 \nonumber$.
1. Скільки часу знадобиться, щоб ракета досягла своєї максимальної висоти?
2. Якої максимальної висоти досягне ракета?
3. Скільки триватиме переліт?
Показати, що з усіх прямокутників заданого периметра прямокутник з найбільшою площею є квадратом.
Показати, що з усіх прямокутників заданої області прямокутник з найменшим периметром є квадратом.
Едуардо хоче побудувати паркан, який захистить його прямокутний томатний сад від різних голодних тварюк, що бродять по ландшафту. Він купує 100 футів паркану. Якими повинні бути розміри томатного саду, якщо він повинен мати максимальну площу, яку можна містити 100 футів паркану.
Гансу було запропоновано знайти два невід'ємних числа, сума яких дорівнює 36, щоб добуток двох чисел був максимальним. Як він повинен вчинити?
Люсії потрібно знайти два невід'ємні числа, твір яких дорівнює 25 таким чином, щоб сума одного плюс квадрат іншого була зведена до мінімуму, щоб отримати членство в клубі. Які цифри вона після?
Есмеральда хоче обкласти поле прямокутним парканом, щоб утримати її кіз від втечі. Одна сторона поля впритул до будівлі, тому вона не зажадає огорожі. Вона має 50 футів огороджувального матеріалу. Які розміри максимальної площі вона може загородити?
Яка точка на графіку функції$ y=\sqrt{x} \nonumber$ найближча до точки (1, 0)?

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 4.9.

Лексика

Термін	Визначення
здійсненний домен	Допустимий домен - це підмножина області первинної функції, яка може бути використана. Цей обмежений домен визначається обмеженнями задачі оптимізації.
оптимальне значення	Оптимальне значення або рішення є найкращим рішенням проблеми оптимізації.
оптимізація	Оптимізаційна задача - це проблема пошуку найкращого рішення проблеми з усіх можливих рішень.
первинне рівняння	Первинним рівнянням задачі оптимізації є функція або рівняння, для яких шукається оптимальне значення або рішення.
вторинне рівняння	Вторинне рівняння - одне з рівнянь, яке використовується для зв'язку змінних задачі та зменшення кількості змінних у первинному рівнянні.