6.3: Похідні експоненціальних функцій

Last updated
Save as PDF

Page ID: 54334

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Експоненціальні функції та швидкість зміни використовуються для моделювання багатьох реальних ситуацій, таких як зростання населення, радіоактивний розпад періоду напіврозпаду, ослаблення електромагнітних сигналів у засобах масової інформації та фінансові операції. Чи знаєте ви, як написати загальні експоненціальні рівняння для зростання популяції, яка подвоюється кожні 5 років, та її темпи зміни?

Похідні експоненціальних функцій

Експоненціальна функція\( f(x) \nonumber\) має вигляд:

\[ f(x) = b^x \nonumber\]

де b називається базовим і є додатним, дійсним числом.

На малюнку нижче показано кілька графіків експоненціальних функцій для 0 <b≤10. Дуже зрозуміло, що знак похідної експоненціальної залежить від значення b, якщо 0<b<1, значення похідної функції (нахил дотичної лінії) буде від'ємним, оскільки функція завжди зменшується зі збільшенням x. Для b>1 похідна функції завжди буде позитивною, оскільки функція збільшується зі збільшенням x.

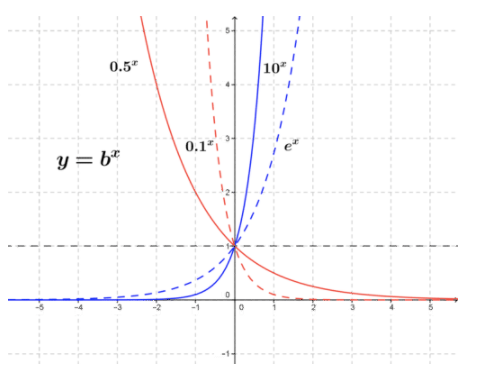
Знімок екрана 2020-11-12 о 11.45.54 PM.png

CC ЗА NC-SA

Але, що таке похідна від експоненціальної функції? Ми можемо зробити наступні кроки, щоб знайти вираз для,\( \frac{d}{dx}[bx] \nonumber\) використовуючи визначення похідної:

\( \displaystyle \frac{d}{dx}[bx]= \lim_{h \to 0} \frac{b^{x+h}−b^x}{h} \nonumber\)... Граничне визначення похідної

\( = \lim_{h \to 0} \frac{b^xb^h−b^x}{h} \nonumber\)... Властивість експоненти

\( = \lim_{h \to 0} \frac{b^h−1}{h}⋅b^x \nonumber\)... Факторинг

\( = ( \lim_{h→0} \frac{b^h−1}{h})⋅bx \nonumber\)... Обмеження властивості продукту

Результат вище показує\( \frac{d}{dx}[bx] \nonumber\) залежить від продукту\( \lim_{h→0} \frac{b^h−1}{h} \nonumber\) і вихідної функції. Але що таке\( \lim_{h→0} \frac{b^h−1}{h} \nonumber\)? Існує ряд способів оцінити цю межу, але поки давайте швидко розглянемо поведінку\( \frac{b^h−1}{h} \nonumber\). Цю функцію наведено нижче для кількості значень b , а межа у точках A−E\( h=0 \nonumber\) позначається точками A−E.

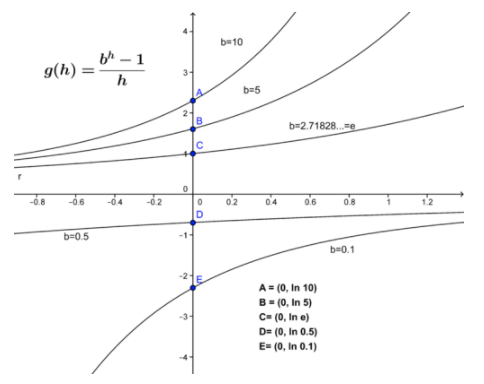
Знімок екрана 2020-11-21 о 6.04.44 PM.png

CC ЗА NC-SA

Поки це зовсім не очевидно:\( \lim_{h→0} \frac{b^h−1}{h} = ln(b) \nonumber\). Пам'ятайте функцію натурального логарифма\( y=lnx \nonumber\) на вашому калькуляторі? Натуральний логарифм - це загальна функція логарифма з основою\( b=e=2.71828 \nonumber\)...

З огляду на експоненціальну функцію\( f(x)=b^x \nonumber\), де основою b є додатне дійсне число, то загальне уявлення похідної експоненціальної функції дорівнює:

\[ \frac{d}{dx}[bx]=lnb⋅b^x \nonumber\]

Додавання правила ланцюга до визначення, заданого експоненціальною функцією f (x) =bu, де u=g (x) та g (x) є диференційованою функцією, то:

\[ \frac{d}{dx}[bu]=(lnb⋅b^u) \frac{du}{dx} \nonumber\]

Приклади

Приклад 1

Раніше вас запитали, що таке загальне експоненціальне рівняння для зростання населення, яке подвоюється кожні 5 років.

Населення\( P(t) \nonumber\), яке подвоюється кожні 5 років, може бути змодельовано як\( P(t)=P_02^{\frac{t}{5}} \nonumber\), де змінна t представляє кількість років, оскільки населення перебувало на рівні\( P_0 \nonumber] \nonumber\). Чи змогли ви визначити, що швидкість зміни\( P(t) \nonumber\) є\( P′(t) = \frac{P_0 ln2}{5}⋅2^{\frac{t}{5}} \nonumber\)?

Приклад 2

Враховуючи\( y=500⋅0.7^x \nonumber\), що таке\( \frac{dy}{dx} \nonumber\)?

\[ \frac{dy}{dx}=\frac{d}{dx}[500⋅0.7^x] \nonumber\]

\[ = 500 \frac{d}{dx}[0.7^x] \nonumber\]

\( = 500[ln(0.7)⋅0.7^x] \nonumber\)... Використовуйте калькулятор, щоб знайти ln (0.7)

\[ =−178.3⋅0.7^x \nonumber\]

Отже, і\( \frac{dy}{dx} =−178.3⋅0.7^x \nonumber\), як і очікувалося, нахили всіх дотичних ліній негативні.

Є важливий особливий випадок, про який ви повинні знати

Приклад 3

Враховуючи\( y=500⋅e^x \nonumber\), що таке\( \frac{dy}{dx} \nonumber\)?

\[ \frac{dy}{dx}= \frac{d}{dx}[500⋅ex] \nonumber\]

\[ = 500 \frac{d}{dx}[ex] \nonumber\]

\( \frac{dy}{dx}=500[ln(e)⋅ex] \nonumber\)... Використовуйте калькулятор, щоб знайти ln (e)

\[ = \frac{d}{dx}[500⋅ex] \nonumber\]

\[ =500[1⋅ex] \nonumber\]

\[ =500⋅ex \nonumber\]

Значить\( \frac{dy}{dx}=500⋅ex \nonumber\), і це тільки оригінальна функція. Ця експоненціальна функція з основою e є особливою: швидкість зміни (або нахил лінії танжета) у будь-якій точці дорівнює значенню функції в цій точці.

Приклад 4

Враховуючи\( y=10⋅2.5−3x^2 \nonumber\), що таке\( \frac{dy}{dx} \nonumber\)?

\[ \frac{dy}{dx} = \frac{d}{dx}[10⋅2.5−3x2] \nonumber\]

\[ =10 \frac{d}{dx}[2.5−3x2] \nonumber\]

\[ =10⋅ln(2.5)⋅2.5−3x2⋅ddx[−3x^2] \nonumber\]

\[ =10⋅(0.9162)⋅2.5−3x^2⋅[−6x] \nonumber\]

\[ =−55x⋅2.5−3x^2 \nonumber\]

Тому,\( \frac{dy}{dx} =−55x⋅2.5−3x^2 \nonumber\)

Приклад 5

Враховуючи\( y=500⋅e−2x⋅cos(5πx) \nonumber\), що таке\( \frac{dy}{dx} \nonumber\)?

\[ \frac{dy}{dx}= \frac{d}{dx}[500⋅e−2x⋅cos(5πx)] \nonumber\]

\( =500⋅[ \frac{d}{dx}(e−2x)⋅cos(5πx)+e−2x⋅ \frac{d}{dx}(cos(5πx))] \nonumber\)... Правило продукту

\( =500⋅[ln(e)⋅e−2x \frac{d}{dx}(−2x)⋅cos(5πx)+e−2x⋅(−sin(5πx)⋅ \frac{d}{dx}(5πx))] \nonumber\)... Використовувати правило ланцюга

\( =500⋅[(1)⋅e−2x⋅(−2)⋅cos(5πx)+e−2x⋅(−sin(5πx)⋅5π)] \nonumber\)... Спростити.

\( =−500⋅e−2x[2⋅cos(5πx)+5πsin(5πx)] \nonumber\)... Спростити

Тому,\( \frac{dy}{dx} =−500⋅e−2x[2⋅cos(5πx)+5πsin(5πx)] \nonumber\).

Рецензія

Для #1 -14 знайдіть похідну.

\( y=7^x \nonumber\)
\( y=3^{2x} \nonumber\)
\( y=5^x−3x^2 \nonumber\)
\( y=2^{x^2} \nonumber\)
\( y=e^{x^2} \nonumber\)
\(f(x)= \frac{1}{ \sqrt{πσ}}e^{−αk(x−x0)^2} \nonumber\)де σ, α, x0 і k - константи і σ 0.
\( y=e^{6x} \nonumber\)
\( y=e^{3x^3}−2x^2+6 \nonumber\)
\( y=\frac{e^x−e−x}{e^x+e−x} \nonumber\)
\( y=cos(e^x) \nonumber\)
\( y=e^{−x}3^x \nonumber\)
\( y=3^{−x^2+2x+1} \nonumber\)
\( y=2^x3^x \nonumber\)
\( y=e^{−x}sinx \nonumber\)
Знайти рівняння дотичної\( f(x)=x^3+2e^x \nonumber\) прямої до точки (0, 2).

Огляд (Відповіді)

Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 3.9.

Лексика

Термін	Визначення
похідний	Похідна функції - нахил прямої дотичної до функції в заданій точці на графіку. Позначення для похідної включають f′ (x), dydx, y′, dfdx і\ frac {df (x)} {dx}.
Експоненціальна функція	Експоненціальна функція - це функція, змінна якої знаходиться в експоненті. Загальна форма є\( y=a⋅b^{x−h}+k \nonumber\).