6.2: Супутні тарифи

У концепції неявної диференціації ви дізналися, що, враховуючи зв'язок між двома величинами, можна визначити взаємозв'язок між відповідними темпами зміни. Це часто є неоціненним інструментом у додатках, оскільки він дозволяє нам знайти швидкість зміни певної кількості, пов'язуючи її з іншими величинами, темпи зміни яких відомі (або принаймні легше знайти). Наприклад, якби ви були на місці аварії, де розлив нафти з великого танкера поширюється круговим малюнком, радіус якого, як ви визначаєте, збільшується приблизно на 1 фут в секунду, чи зможете ви сказати комусь, наскільки швидко площа розливу нафти збільшувалася, коли радіус становив близько 30 футів?

---

Пов'язані тарифи

Що ми маємо на увазі під суміжними тарифами? Це просто похідні, ставки, одного або декількох параметрів, які пов'язані один з одним за допомогою рівняння. Зв'язок між ставками виходить шляхом взяття похідної від якоїсь іншої залежності між параметрами.

Простий приклад зі знайомою геометричною формою повинен допомогти проілюструвати концепцію.

Розглянемо простий прямокутний трикутник на малюнку нижче зі сторонами x, y і z Відносини між сторонами регулюється теоремою Піфагора.

$$x^2+y^2=z^2 \nonumber$$

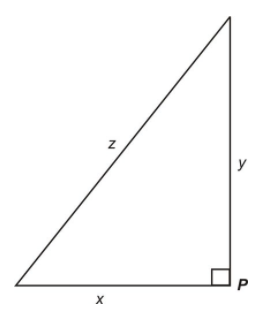
CC ЗА NC-SA

Ми могли б легко прикріпити деяку реальну ситуацію до цієї геометричної фігури. Скажімо, наприклад, що x і y представляють шляхи двох людей, починаючи з точки р і йдучи на північ і захід, відповідно, протягом двох годин. Величина z представляє відстань між ними в будь-який час t Тепер визначимо будь-які відносини між різними швидкостями зміни, які ми отримуємо, неявно диференціюючи початкове рівняння x ² +y ^{2 = z 2} щодо часу t.

$$\frac{d}{dt}[x^2+y^2]=\frac{d}{dt}[z^2] \nonumber$$

$$2x\frac{dx}{dt}+2y\frac{dy}{dt}=2z\frac{dz}{dt} \nonumber$$

$$x\frac{dx}{dt}+y\frac{dy}{dt}=z\frac{dz}{dt} \nonumber$$

... Рівняння 1

Неявна диференціація піфагора відносини між довжинами сторін дала відносини між похідними довжини сторони, і оскільки похідні є ставками, це приклад пов'язаних ставок.

Як можуть бути використані вище відносини для вирішення або відповіді на проблему?

Скажімо, що людина йде в напрямку x зі швидкістю 5 миль/год, і що інша людина йде в напрямку y зі швидкістю 3 миль/год. Відстань, z, між ходунками змінюється з часом, а часова швидкість зміни of, z, ^dz/_dt, залежить від швидкості, з якою йдуть дві людини.

Однією з проблем, яку ми могли б поставити, є:

З якою швидкістю відстань між x і y збільшується через одну годину? Тобто що таке dzdt через одну годину?

Припустимо, що вони гуляли протягом однієї години. Так х = 5 ми і у = 3.

Використовуючи теорему Піфагора, знаходимо відстань між ними через одну годину $$z=\sqrt{34}=5.83 \nonumber$$

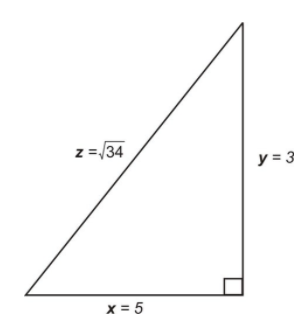
CC ЗА NC-SA

Якщо ми підставимо значення для x, y та z в Рівняння 1 разом з індивідуальними ставками, ми отримаємо

$$5(5)+3(3)=\sqrt{34}\frac{dz}{dt} \nonumber$$

$$34=\sqrt{34}\frac{dz}{dt} \nonumber$$

$$\frac{34}{\sqrt{34}}=\frac{dz}{dt} \nonumber$$

Отже, через одну годину відстань між двома людьми збільшується зі швидкістю:

$$\frac{dz}{dt}=\frac{34}{\sqrt{34}}≈5.83 mph \nonumber$$

Припустимо, у нас прямокутне поле і ми знаємо, що в один момент часу довжина змінюється зі швидкістю 8 футів/год і периметр змінюється зі швидкістю 24 футів/год. З якою швидкістю змінюється ширина в цей момент? З якою швидкістю змінюється площа в цей момент?

Ви знайомі з формулами периметра:

$$P=2l+2w \nonumber$$

Якщо ми диференціюємо рівняння периметра, ми маємо

Рівняння 2: $$\frac{dP}{dt}=2\frac{dl}{dt}+2\frac{dw}{dt} \nonumber$$

Підставляючи нашу відому інформацію в рівняння 2, ми маємо

$$24=(2×8)+2×\frac{dw}{dt} \nonumber$$

$$8=2×\frac{dw}{dt} \nonumber$$

$$4=\frac{dw}{dt} \nonumber$$

Ширина змінюється зі швидкістю 4 футів/год.

---

Приклади

Приклад 1

Раніше вас запитали про те, щоб опинитися на місці аварії, де розлив нафти з великого танкера поширюється круговим малюнком, радіус якого, як ви визначаєте, збільшується приблизно на 1 фут в секунду. Чи могли б ви сказати комусь, як швидко збільшувалася площа розливу нафти, коли радіус становив близько 30 футів?

Оскільки кругова площа розливу є $$A=πr^2 \nonumber$$ часовою швидкістю зміни площі, $$\frac{dA}{dt}=π2r\frac{dr}{dt} \nonumber$$ це означає, що $$\frac{dr}{dt}=1 \frac{ft}{s} \nonumber$$ при r=30 футів, $$\frac{dA}{dt}=60π \frac{ft^2}{s} \nonumber$$

Приклад 2

У нас є резервуар для води у формі перевернутого правого кругового конуса. Припустимо, що вода надходить в бак зі швидкістю 5 фт3/хв. З якою швидкістю піднімається рівень води, коли висота води в баку становить 6 футів?

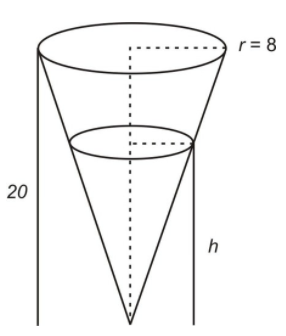
CC ЗА NC-SA

Ми знаємо, що обсяг води в резервуарі для води становить:

$$V=\frac{1}{3} \pi r^2h \nonumber$$

Коли ми диференціюємо це рівняння, ми отримуємо:

$$\frac{dV}{dt}=\frac{1}{3} \pi (h)(2r)\frac{dr}{dt}+\frac{1}{3} \pi r^2\frac{dh}{dt} \nonumber$$

Це пов'язане рівняння ставок. Швидкість ^_dV/dt пов'язана зі ставками ^dr/dt _{і ^dh /dt}.

Ми знаємо, що $$\frac{dV}{dt}=5 \frac{ft^3}{min} \nonumber$$ не знаємо ^_dr/dt, але хочете знайти ^_dh/dt. Потрібно якось знайти зв'язок між h і r.

Нехай r1 - радіус поверхні води, коли вона витікає з резервуара.

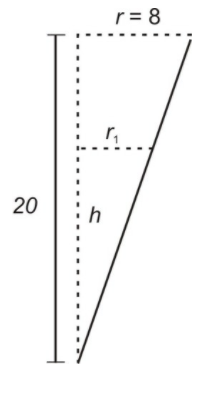
CC ЗА NC-SA

Зверніть увагу, що два трикутника схожі і, таким чином, відповідні частини пропорційні. Зокрема,

$$\frac {r_1}{h} = \frac{8}{20} \nonumber$$

$$r_1 = \frac{8h}{20} = \frac{2h}{5} \nonumber$$

Ми можемо написати це як загальний зв'язок між r і h.

$$r = \frac{2h}{5} \nonumber$$

що також означає, що

$$\frac{dr}{dt} =\frac{2}{5} \frac{dh}{dt} \nonumber$$

У нас є потрібні нам відносини.

Тепер ми можемо вирішити проблему парою способів: (а) підставити

$$r = \frac{2h}{5} \nonumber$$ у вихідне рівняння для V, або (b) заміни

$$r = \frac{2h}{5} \nonumber$$ і

$$\frac{dr}{dt} =\frac{2}{5} \frac{dh}{dt} \nonumber$$ у рівняння для $$\frac{dV}{dt} \nonumber$$

Спробуємо підхід (а).

$$V = \frac{1}{3} \pi (\frac{2h}{5})^2 h = \frac{4 \pi}{75} h^3 \nonumber$$

Звідси

$$\frac{dV}{dt} = \frac{12 \pi}{75} h^2 \frac{dh}{dt} \nonumber$$

і шляхом підміни,

$$5 = \frac{12 \pi}{75} (36) \frac{dh}{dt} \nonumber$$

$$\frac{dh}{dt} = \frac{375}{432 \pi} \approx 0.28 \frac{ft}{min} \nonumber$$

---

Рецензія

1. Складіть пов'язану задачу ставок про площу прямокутника. Проілюструйте рішення вашої проблеми.
2. Припустимо, що частинка рухається по кривій 4x ² +16y ² =32. Коли вона досягає точки (2, 1), координата x збільшується зі швидкістю 3 футів/сек. З якою швидкістю y-координата змінюється в цей момент?
3. Регулювання софтболу діамант - це квадрат з кожної сторони довжиною 60 футів. Припустимо, гравець працює від першої бази до другої бази зі швидкістю 18 футів/сек. З якою швидкістю змінюється відстань між бігуном та домашньою пластиною, коли бігун становить ^_2/3 шляху від першої до другої основи?
4. На недавньому фестивалі Hot Air Balloon був випущений повітряна куля. Досягнувши висоти 300 футів, він піднімався зі швидкістю 20 футів/сек. Містер Сміт знаходився на відстані 100 футів від місця запуску, спостерігаючи за повітряною кулею. З якою швидкістю відстань між містером Смітом і повітряною кулею змінювалася в той момент?
5. Два поїзди пішли з залізничного вокзалу Сент-Луїса пізно вранці. Перший поїзд їхав на схід з постійною швидкістю 65 км/год. Другий поїзд їхав на південь з постійною швидкістю 75 км/год. О 15:00 перший поїзд проїхав відстань 120 миль, тоді як другий поїзд проїхав відстань 130 миль. Наскільки швидко змінювалася відстань між двома поїздами в той час?
6. Припустимо, що 17 футів сходи ковзають вниз по стіні зі швидкістю -6 футів/сек. З якою швидкістю рухається низ сходів, коли верх знаходиться на відстані 8 футів від землі?
7. Припустимо, що довжина прямокутника збільшується зі швидкістю 6 футів/хв, а ширина збільшується зі швидкістю 2 футів/хв. З якою швидкістю змінюється площа прямокутника, коли його довжина становить 25 футів, а ширина 15 футів?
8. Припустимо, що кількісний попит нових 40′′ плазмових телевізорів пов'язаний з його ціною одиниці за формулою p+x ² =1200, де p вимірюється в доларах, а x вимірюється в одиницях однієї тисячі. Як змінюється попит на кількість, коли x = 20, p = 1500, а ціна за телевізор знижується зі швидкістю 10 доларів?
9. Обсяг куба зі стороною s змінюється. У певний момент сторони куба становлять 6 дюймів і збільшуються зі швидкістю ^_1/4 в/хв. Наскільки швидко збільшується обсяг куба в той час?
10. (1) Припустимо, що площа кола збільшується зі швидкістю 24 в ² /хв. Як швидко радіус збільшується, коли площа 36π в ²? (2) Наскільки швидко змінюється окружність в цей момент?
11. Радіус кола стає більше зі швидкістю 5 сантиметрів в секунду. Як швидко збільшується площа кола, коли радіус дорівнює десяти сантиметрам?
12. Площа кола розширюється зі швидкістю 100 квадратних сантиметрів в секунду в одну мить, коли його радіус розширюється зі швидкістю 50 сантиметрів в секунду. Який радіус кола в цей момент?
13. У даний момент обсяг циліндра з площею поперечного перерізу 6 квадратних сантиметрів збільшується зі швидкістю 10 кубічних сантиметрів в секунду. Яка швидкість збільшення його висоти в цей момент?
14. Висловлюйте швидкість зміни об'єму циліндра в залежності від його радіуса, висоти та швидкості зміни його радіуса, якщо його висота вважається постійною.
15. Чотиривимірний об'єкт, імпульс якого задається формулою,\[ M=sin( \pi x_1)+δx_2^3+ln(x_3x_4)x_1^5, where delta is a constant, is falling into a black hole. The resulting compression causes its x₁ value to shrink at a rate of 8 million miles a second (while the other variables remain constant.) If $$x_3= \frac{5}{x_4} \nonumber$$ яка миттєва зміна його імпульсу, коли х ₁ = 1?

---

Огляд (Відповіді)

Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 4.1.

---

Лексика

Термін	Визначення
похідний	Похідна функції - нахил прямої дотичної до функції в заданій точці на графіку. Позначення для похідної включають f′ (x), dydx, y′, dfdx і\ frac {df (x)} {dx}.
пов'язані тарифи	Пов'язані ставки - це похідні змінних, які є загальними (пов'язаними) з одним або декількома пов'язаними рівняннями.

---

Додатковий ресурс

Відео - Проблема швидкості зміни сходів

Практика - Пов'язані тарифи

Реальний світ - ланцюгова реакція