3.1: Неперервність функції
- Page ID
- 54371
Неперервність функції пов'язана з концептуальним поняттям функції, яка не має перерв або раптових стрибків, оскільки незалежна змінна приймає всі значення протягом деякого інтервалу. Немає прогалин діапазону або раптових стрибків через цікаву область. Маючи це на увазі, подивіться, чи зможете ви визначити, що з наступного можна вважати неперервною функцією:
- щоденна зміна температури зовнішнього повітря
- вага візка, як на неї завантажуються 10 фунтів мішки піску
- підйом і падіння рівня водойми
- сума грошей, зібраних в кінотеатрі за конкретний показ.
Безперервність
Неперервність функції концептуально є характеристикою кривої функції, яка має значення діапазону «потоку» безперервно без перерви протягом деякого інтервалу, як ніби ніколи не потрібно піднімати олівець з паперу під час малювання кривої. Це інтуїтивне поняття потрібно формалізувати математично.
Розглянемо графік функції f (x) =x 2. Функція визначається для будь-якого дійсного значення незалежної змінної.
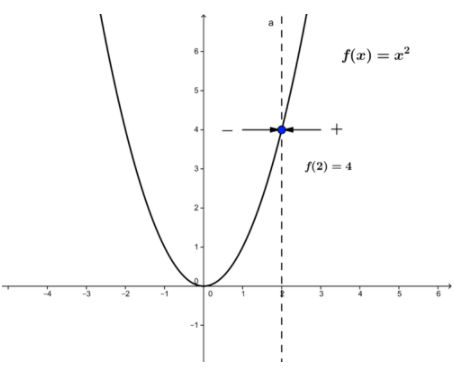
Фонд CK-12 - CC BY-NC-SA
Наприклад, для x=2 функція має значення f (2) =4. Зверніть увагу, що коли х наближається до значення 2 або зліва, або справа, значення функції наближається до 4, тобто
\[\lim _{x \rightarrow 2} f(x)=f(2)=4\]
Концептуально застосування лівої та правої односторонніх меж, коли х наблизився до 2, призвело до того ж значення, значення функції при x=2.
Наведені вище результати ілюструють ключові властивості неперервної функції. Вони формалізовані в наступному визначенні, яке забезпечує тест на визначення того, коли ми маємо безперервну функцію.
Функція f (x) є неперервною при x = a, якщо всі умови виконуються:

Зауважте, що можна мати функції, де виконуються дві з цих умов, а третя - ні. Коли функція не є безперервною при x = a, то вона переривається в a, а є точкою розриву.
Розглянемо кускову функцію
\ [f (x) =\ лівий\ {\ begin {масив} {l}
x,\ текст {якщо} x\ neq 1\\
3,\ текст {якщо} x=1
\ end {масив}\ справа.\]
з графіком, показаним нижче.
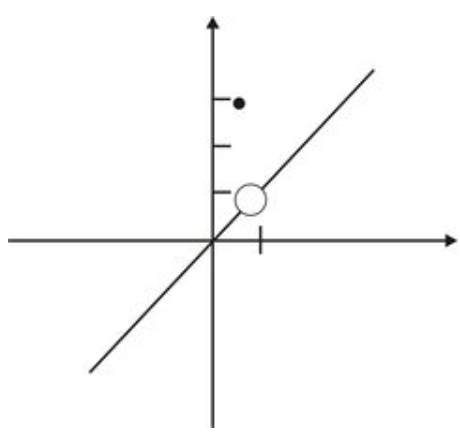
Фонд CK-12 - CC BY-NC-SA
У цьому прикладі ми маємо
\[\lim _{x \rightarrow 1} f(x)\]
існує! Значення x=1 знаходиться в області f (x), але
\[\lim _{x \rightarrow 1} f(x) \neq f(1)\]
Тому функція не є безперервною при x = 1.
Це приклад знімного розриву, тобто розриву, при якому межа функції існує, але не дорівнює значенню функції в цій точці.
Розглянемо наступну функцію:
\[f(x)=\frac{(x+1)}{\left(x^{2}-1\right)}\]
Чи є якісь розриви?
З нашого дослідження доменів ми знаємо, що для того, щоб функція була визначена, ми повинні мати x−1,1. Але коли ми генеруємо графік функції (за допомогою стандартного вікна перегляду), ми отримуємо наступну картинку, яка, здається, визначається у x=−1:
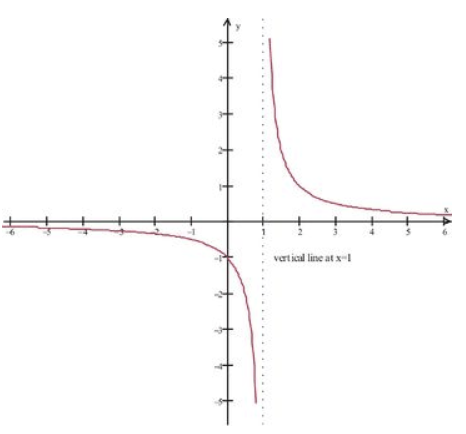
Фонд CK-12 - CC BY-NC-SA
Очевидне протиріччя пов'язано з тим, що наша вихідна функція мала x+1 як загальний коефіцієнт у чисельнику та знаменнику, який скасував і дав нам картину, яка здається графіком
\[f(x)=\frac{1}{(x-1)}\]
Але те, що ми насправді є оригінальною функцією,
\[f(x)=\frac{(x+1)}{\left(x^{2}-1\right)}\]
що, як ми знаємо, не визначено у x=−1. У x=−1 ми маємо дірку у графі, або розрив функції при x=−1. Тобто функція визначається для всіх інших значень x, близьких до x=−1.
Крім того, при x=1 значення функції доходять до ±∞ залежно від того, яка сторона x=1 використовується. Правий і лівий односторонні межі не будуть однаковими, а функція переривається при x = 1. Розрив при x=1 називається нескінченним розривом і пов'язаний з вертикальною асимптотою x=1.
Вільно кажучи, якби ми вручну намалювали графік, нам потрібно було б зняти олівець зі сторінки, коли ми дісталися до цього отвору, залишивши прогалину в графіку, як зазначено:
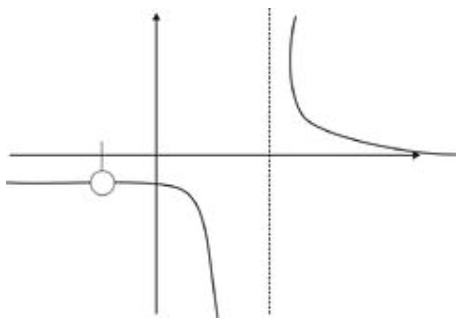
Фонд CK-12 - CC BY-NC-SA
Приклади
Приклад 1
Раніше вас запитали, що з наведених нижче можна вважати неперервною функцією:
- щоденна зміна температури зовнішнього повітря
- вага візка при завантаженні 10 фунтів мішків з піском
- підйом і падіння рівня води у водоймі
- сума грошей, зібраних в кінотеатрі за конкретний показ
Щоденну зміну температури на відкритому повітрі можна вважати безперервною функцією часу, оскільки всі значення температури відбуваються в діапазоні змін.
Вага візка, оскільки завантажуються мішки піску 10 фунтів, не буде вважатися безперервною функцією кількості мішків, оскільки можливі лише цілі числа мішків, а загальна вага змінюється з кроком 10 фунтів, тому є зазори.
Підйом і падіння рівня води у водоймі можна вважати безперервною функцією часу, оскільки всі рівні відбуваються в діапазоні варіацій.
Сума грошей, зібраних у кінотеатрі для конкретного показу, не вважатиметься безперервною функцією, оскільки кількість людей, які купують та ціна за квиток, є цілими числами, так що можливі лише певні загальні суми в доларах.
Приклад 2
Знайдіть значення k, яке робить наступну функцію неперервною:
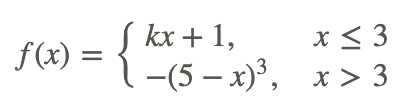
Якщо f (x) слід вважати безперервним скрізь, він повинен бути безперервним при x = 3. Це означає, що:

Тоді
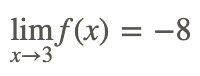
З вищенаведеним результатом ми маємо
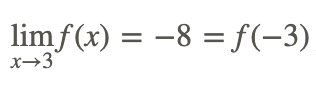
Тому функція
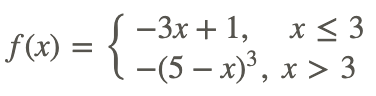
є безперервним при x = 3.
Приклад 3
Згадаймо нашу основну функцію квадратного кореня, f (x) = x 0.5, показану нижче. Це безперервно при x = 0?
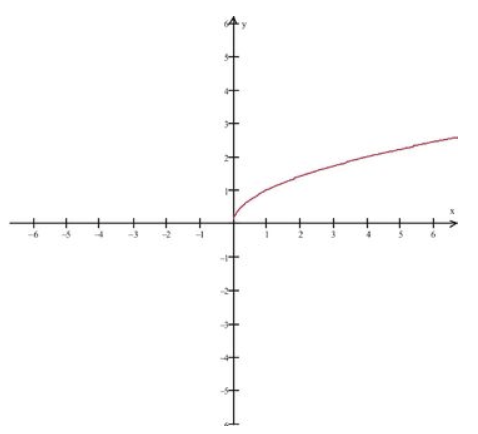
Фонд CK-12 - CC BY-NC-SA
Оскільки домен f (x) = x 0.5 дорівнює x≥0, ми бачимо, що
\[\lim _{x \rightarrow 0} \sqrt{x}\]
не існує. Зокрема, ми не можемо знайти відкриті інтервали навколо\(x=0\), які задовольняють визначенню межі. Тому функція не є безперервною при\(x=0\). Однак ми зауважимо, що коли ми наближаємося до x = 0 з правого боку, ми бачимо послідовні значення, що прагнуть до\(x=0\).
Рецензія


Огляд (Відповіді)
Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 2.9.
Лексика
| Термін | Визначення |
|---|---|
| Безперервний | Безперервність для точки існує, коли ліві та праві межі збігаються з функцією, оціненою в цій точці. Щоб функція була неперервною, функція повинна бути неперервною в кожній точці нерозривної області. |
| Безперервна функція | Безперервна функція - це функція без розривів або зазорів. Він містить нескінченну, незліченну кількість значень. |
| розривів | Точками розриву функції є вхідні значення функції, де функція є переривчастою. |
| переривчастий | Функція є переривчастою, якщо функція виявляє розриви або дірки при графіку. |
| переривчастий в точці | Функція є переривчастою в точці a, якщо функція не визначена в x = a. |
| Нескінченні розриви | Нескінченні розриви виникають, коли функція має вертикальну асимптоту з однієї або обох сторін. Це станеться, коли коефіцієнт в знаменнику функції дорівнює нулю. |
| Нескінченний розрив | Нескінченні розриви виникають, коли функція має вертикальну асимптоту з однієї або обох сторін. Це станеться, коли коефіцієнт в знаменнику функції дорівнює нулю. |
| точки розриву | Точками розриву функції є вхідні значення функції, де функція є переривчастою. |
| Знімні розриви | Знімні розриви також відомі як отвори. Вони виникають, коли фактори можуть бути алгебраїчно скасовані від раціональних функцій. |
| Знімний розрив | Знімні розриви також відомі як отвори. Вони виникають, коли фактори можуть бути алгебраїчно скасовані від раціональних функцій. |
Додаткові ресурси
PLIX: Грайте, вчіться, взаємодійте, досліджуйте - безперервність
Відео: Безперервність за допомогою лімітів
Практика: Неперервність функції
Реальний світ: Мітохондріальна ДНК