9.27: Обсяг сфер
- Page ID
- 54488

У Марії є прес-пап'є, що представляє собою скляну сферу. Сфера наповнена рідиною. Якщо діаметр прес-пап'є становить 6 дюймів, скільки рідини воно містить?
У цьому понятті ви навчитеся обчислювати обсяг сфер.
Обсяг
Об'єм - це міра тривимірного простору, який займає фігура. Ви також можете думати про це як про те, скільки місця «тримає» фігура.
Щоб знайти обсяг сфер, можна використовувати піраміди. Уявіть собі піраміду з її основою на поверхні сфери та її точкою як центром сфери. Радіус сфери буде висотою піраміди.
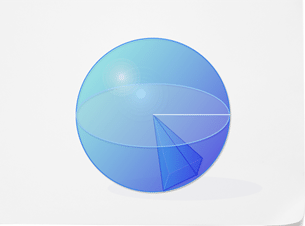
Піраміда становить частину обсягу сфери. Якщо ви можете заповнити всю сферу такими пірамідами, ви б знали обсяг сфери. Вона дорівнювала б обсягам всіх пірамід, зібраних разом. Скільки пірамід потрібно, щоб заповнити сферу? Це залежить від площі поверхні сфери.
Ви можете об'єднати площу поверхні сфери з формулою об'єму для піраміди, щоб обчислити об'єм усіх пірамід, що містяться в сфері.
Формула для обсягу піраміди є\(V=\dfrac{1}{3}Bh\).
Ви знаєте, що висота піраміди - це радіус (r) сфери, а основа піраміди - площа поверхні сфери (\(SA=4\pi r^2\)). Якщо ви підставите цю інформацію в формулу для обсягу піраміди, ви отримаєте наступне.
\(\begin{aligned}V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(4\pi r^{2})r \\ V&=\dfrac{4}{3} \pi r^{3}\end{aligned}\)
Обсяг сфери можна знайти за формулою
\(V=\dfrac{4}{3}\pi r^{3}\)
Знову ж таки, все, що вам потрібно знати, це радіус сфери. Ви ставите значення в for r у формулі і вирішуєте for\(V\), обсяг.
Давайте розглянемо приклад.
Знайдіть обсяг сфери нижче.
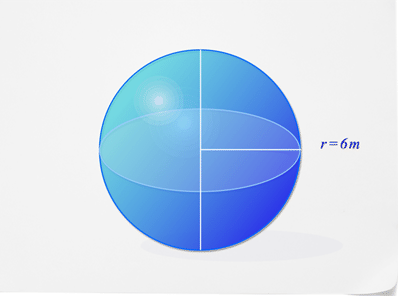
По-перше, підставляйте те, що ви знаєте, у формулу обсягу.
\(\begin{aligned} V&=\dfrac{4}{3}\pi r^{3} \\ V&=\dfrac{4}{3}\pi (6)^{3}\end{aligned}\)
Далі використовуйте алгебру для обчислення обсягу.
\(\begin{aligned} V&=\dfrac{4}{3}\pi (6)^{3} \\ V&=\dfrac{4}{3}\pi (216) \\ V&=288\pi \\ V&=904.78\end{aligned}\)
Відповідь - 904,78.
Обсяг сфери - це\(904.78 \text{ m}^{3}\).
Якщо ви хотіли зробити своє вимірювання більш точним, ви могли б сказати, що обсяг є\(288\pi m^{3}\).
Приклад\(\PageIndex{1}\)
Раніше вам давали проблему з приводу рідкого прес-пап'є Марії.
У Марії є прес-пап'є діаметром 6 дюймів, яка наповнена водою, і вона хоче дізнатися, скільки рідини всередині.
Рішення
Спочатку знайдіть радіус сфери. Пам'ятайте, що радіус дорівнює половині діаметра.
\(\begin{aligned}r&=\dfrac{d}{2} \\ r&=\dfrac{6}{2} \\ r&=3 \end{aligned}\)
Далі підставте те, що ви знаєте, в формулу обсягу.
\(\begin{aligned}V&=\dfrac{4}{3}\pi r^{3} \\ V&=\dfrac{4}{3}\pi (3)^{3}\end{aligned}\)
Потім використовуйте алгебру для обчислення обсягу.
\(\begin{aligned} V&=\dfrac{4}{3}\pi (3)^{3} \\ V&=\dfrac{4}{3}\pi \\ V&=(27)^{3}6\pi \\ V&=113.10v\end{aligned}\)
Відповідь - 113.10.
Обсяг, що міститься в прес-пап'є Марії, є\(113.10 \text{ in}^{3}\) або\(36\pi \text{ in}^{3}\).
Приклад\(\PageIndex{2}\)
Знайдіть обсяг наступної сфери.

Рішення
По-перше, підставляйте те, що ви знаєте, у формулу обсягу.
\(\begin{aligned}V&=\dfrac{4}{3}\pi r^{3} \\ V&=\dfrac{4}{3}\pi (8)^{3}\end{aligned}\)
Далі використовуйте алгебру для обчислення обсягу.
\(\begin{aligned}V&=\dfrac{4}{3}\pi (8)^{3} \\ V&=\dfrac{4}{3}\pi (512) \\ V&=682.67\pi \\ V&=2144.66\end{aligned}\)
Відповідь - 2144.66. Обсяг сфери - це\(2144.66 cm^{3}\).
Якщо ви хотіли зробити своє вимірювання більш точним, ви могли б сказати, що обсяг є\(682.67\pi cm^3\).
Приклад\(\PageIndex{3}\)
Знайдіть обсяг сфери радіусом 4 дюйми.
Рішення
По-перше, підставляйте те, що ви знаєте, у формулу обсягу.
\(\begin{aligned}V&=\dfrac{4}{3}\pi r^{3} \\ V&=\dfrac{4}{3}\pi (4)^{3}\end{aligned}\)
Далі використовуйте алгебру для обчислення обсягу.
\(\begin{aligned}V&=\dfrac{4}{3}\pi (4)^{3} \\ V&=\dfrac{4}{3}\pi (64) \\ V&=85.33\pi \\ V&=268.08\end{aligned}\)
Відповідь - 268.08.
Обсяг сфери - це\(268.08 \text{ in}^{3}\).
Приклад\(\PageIndex{4}\)
Знайдіть об'єм сфери радіусом 5 футів.
Рішення
По-перше, підставляйте те, що ви знаєте, у формулу обсягу.
\(\begin{aligned}V&=\dfrac{4}{3}\pi r^{3} \\ V&=\dfrac{4}{3}\pi (5)^{3}\end{aligned}\)
Далі використовуйте алгебру для обчислення обсягу.
\(\begin{aligned}V&=\dfrac{4}{3}\pi (5)^{3} \\ V&=\dfrac{4}{3}\pi (125) \\ V&=166.67\pi \\ V&=523.60\end{aligned}\)
Відповідь - 523.60.
Обсяг сфери - це\(523.60 \: ft^{3}\).
Приклад\(\PageIndex{5}\)
Знайдіть обсяг сфери радіусом 3,5 дюйма.
Рішення
По-перше, підставляйте те, що ви знаєте, у формулу обсягу.
\(\begin{aligned}V&=\dfrac{4}{3}\pi r^{3} \\ V&=\dfrac{4}{3}\pi (3.5)^{3}\end{aligned}\)
Далі використовуйте алгебру для обчислення обсягу.
\(\begin{aligned} V&=\dfrac{4}{3}\pi (3.5)^{3} \\ V&=\dfrac{4}{3}\pi (42.875) \\ V&=57.17\pi \\ V&=179.59\end{aligned}\)
Відповідь - 179,59.
Обсяг сфери - це\(179.59 \text{ in}^{3}\).
Рецензія
Знайдіть обсяг кожної сфери. Ви можете округлити до найближчих сотих, коли це необхідно.
1. Сфера радіусом 3 м.
2. Сфера радіусом 2,5 м.
3. Сфера радіусом 5 дюймів.
4. Сфера радіусом 6 дюймів.
5. Сфера радіусом 7 футів.
6. Сфера радіусом 4,5 см.
7. Сфера радіусом 5,5 м.
8. Сфера радіусом 13 мм.
9. Сфера діаметром 8 дюймів.
10. Сфера діаметром 10 футів.
11. Сфера діаметром 3 м.
12. Сфера діаметром 13 м.
13. Сфера діаметром 22 фути.
Використовуйте те, що ви навчилися, щоб вирішити кожну проблему.
14. Сфера має діаметр 12 футів. Який її обсяг?
15. У Келлі флакон духів у формі кулі. Діаметр пляшки - 6 дюймів. Скільки парфумів залишилося Келлі, якщо флакон заповнений лише наполовину?
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 8.15.
Лексика
| Термін | Визначення |
|---|---|
| Сфера | Сфера - це кругле об'ємне тверде тіло. Всі точки на поверхні сфери рівновіддалені від центру сфери. |
| Обсяг | Об'єм - це кількість простору всередині меж тривимірного об'єкта. |
Додаткові ресурси
Відео: Обсяг сфери
Практика: Обсяг сфер