9.23: Площа поверхні конусів
- Page ID
- 54495
ПОТРІБЕН КОНТЕНТ З GEO.858

Роббі будує підставу для циліндричного вентилятора, щоб поставити в своїй кімнаті. Зрізаний конус має більший радіус 3 фути, менший радіус 2 фути та висоту нахилу 3 фути. Він збирається фарбувати підставку і потрібно знайти площу поверхні підстави, щоб з'ясувати, скільки фарби купувати. Як Роббі може з'ясувати площу поверхні?
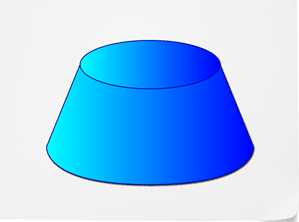
У цьому понятті ви навчитеся знаходити площу поверхні конусів і усічених конусів.
Площа поверхні
Конуси - це об'ємні фігури, які мають круглу основу і точку вгорі. Розрахувати площу поверхні конуса можна за допомогою сітки або формули. Площа поверхні - це загальна площа кожної грані в суцільному малюнку.
Ось як виглядала б сітка конуса.

Заштриховане коло є основою. Пам'ятайте, шишки завжди мають круглі підстави. Незатінена частина конуса представляє його сторону. Технічно ви не називаєте це обличчям, оскільки воно має круглий край.
Щоб знайти площу поверхні конуса, потрібно обчислити площу круглого підстави і збоку і скласти їх разом. Формула знаходження площі кола дорівнює\(A&=\pi r^{2}\), де r - радіус кола. Ви використовуєте цю формулу, щоб знайти площу круглої основи.
Щоб знайти площу сторони конуса, помножте радіус (\(r\)), висоту нахилу (\(s\)) та\(\pi\).
\(A=\pi rs\)
Давайте розглянемо приклад.
Знайдіть площу поверхні наступного конуса.
 Малюнок\(\PageIndex{4}\)
Малюнок\(\PageIndex{4}\)Спочатку розрахуйте площу підстави.
\(\begin{aligned}A&=\pi r^{2} \\ A&=\pi (5)^{2}\\ A&=78.5\end{aligned}\)
Далі обчислити площу сектора, також відому як площа бічної поверхні.
\(\begin{aligned}A&=\pi (5)(11.7) \\ A&=183.8\end{aligned}\)
Потім додайте площу підстави до площі бічної поверхні.
\(\begin{aligned} A&=\text{base} +\text{lateral Surface} \\ A&=78.5+183.8 \\ A&=262.3\end{aligned}\)
Відповідь - 262.3.
Площа поверхні конуса дорівнює\(262.3 \text{ in}^{2}\).
Коротким розрізом було б просто використовувати формулу, щоб знайти площу поверхні конуса. Ось формула знаходження площі поверхні конуса:\(SA&=\pi r^{2}+\pi rs\).
Перша частина формули - це просто формула площі для кіл.\(\pi r^{2}\) Це являє собою базову площу. Друга частина,\ pi rs, являє собою площу бічної поверхні сторони конуса. Ви можете просто скласти шматки разом і вирішити для площі обох частин відразу.
Зрізаний конус - це той, де точка конуса відрізається, залишаючи дві кругові підстави і бічну грань.
Нижче наведено зображення того, як виглядає усічений конус.
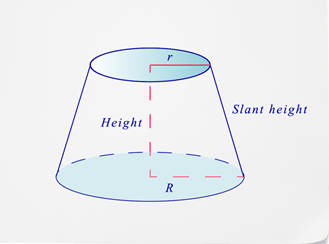
Зверніть увагу, що з усіченим конусом у вас будуть дві різні круглі основи - верхнє радіус і нижнє. Вам доведеться знайти площу обох баз плюс площа сектора, щоб знайти площу поверхні.
Формула знаходження площі поверхні усіченого конуса така:
\(SA=\pi [s(R+r)+r^{2}+r^{2}]\)
Зверніть увагу, що s означає висоту нахилу, капітал R означає більший радіус, а нижній регістр r - менший радіус.
Давайте розглянемо приклад.
Яка площа поверхні усіченого конуса з висотою ухилу 6 см, радіусом 8 см і радіусом 6 см?
Спочатку заповніть все, що ви знаєте, у формулу площі поверхні.
\(\begin{aligned}SA&=\pi [s(R+r)+r^{2}+r^{2}] \\ SA&=\pi [6(8+6)+8^{2}+6^{2}]\end{aligned}\)
Далі використовуйте алгебру для вирішення площі поверхні.
\(\begin{aligned}SA&=\pi [6(8+6)+8^{2}+6^{2}] \\ SA&=\pi [6(14)+64+36] \\ SA&=\pi [84+64+36] \\ SA&=\pi [184] \\ SA&=578.1\end{aligned}\)
Відповідь - 578.1.
Площа поверхні конуса дорівнює\(578.1\text{ cm}^2\).
Приклад\(\PageIndex{1}\)
Раніше вам давали проблему з приводу фанатської стійки Роббі.
Роббі будує підставку у формі усіченого конуса. Нижня кругла основа має радіус 3 фути. Кругла вершина має радіус 2 фути. Висота нахилу для підставки становить 3 фути. Роббі повинен знайти площу поверхні, щоб він знав, скільки фарби йому потрібно.
Рішення
По-перше, підставити те, що ви знаєте, у формулу площі поверхні.
\(\begin{aligned}SA&=\pi [s(R+r)+r^{2}+r^{2}] \\ SA&=\pi [3(3+2)+3^{2}+2^{2}]\end{aligned}\)
Далі використовуйте алгебру для вирішення площі поверхні.
\(\begin{aligned}SA&=\pi [3(3+2)+3^{2}+2^{2}] \\ SA&=\pi [3(5)+9+4] \\ SA&=\pi [15+9+4] \\ SA&=\pi [28] \\ SA&=87.96\end{aligned}\)
Відповідь - 87,96.
Роббі потрібно достатньо фарби для покриття\(88\text{ ft}^2\).
Приклад\(\PageIndex{2}\)
Трей прикрашає конічні капелюхи партії для своєї партії, загорнувши їх у кольоровий цигарковий папір. Кожна капелюшок має радіус 4,2 сантиметра і похилу висоту 8,6 сантиметра. Якщо він хоче обернути шість шапок для вечірок, скільки паперу йому знадобиться?
Рішення
По-перше, підставити те, що ви знаєте, у формулу площі поверхні.
\(\begin{aligned}SA&=\pi r^{2}+\pi rs \\ SA&=\pi (4.2)2+\pi (4.2)(8.6)\end{aligned}\)
Далі використовуйте алгебру для вирішення площі поверхні.
\(\begin{aligned}SA&=\pi (4.2)^{2}+\pi (4.2)(8.6) \\ SA&=\pi (17.64)+\pi (36.12) \\ SA&=55.4+113.5 \\ SA&=168.9\end{aligned}\)
Потім знайдіть загальну площу 6 капелюхів.
\(SA_{total}&=6×SA^{one\: hat} 89 \\ SA_{total}&=6×168.9 \\SA_{total}&=1013.4\end{aligned}\)
Відповідь - 1013,4.
Трею знадобиться 1013,4 см 2 паперу, щоб зробити шість капелюхів.
Приклад\(\PageIndex{3}\)
Знайдіть площу поверхні конуса радіусом 4 дюйми і висотою нахилу 6 дюймів.
Рішення
По-перше, підставити те, що ви знаєте, у формулу площі поверхні.
\(\begin{aligned}SA&=\pi r^{2}+\pi rs \\ SA&=\pi (4)2+\pi (4)(6)\end{aligned}\)
Далі використовуйте алгебру для вирішення площі поверхні.
\(\begin{aligned}SA&=\pi (4)^{2}+\pi (4)(6) \\ SA&=\pi (16)+\pi (24) \\ SA&=50.3+75.4\\ SA&=125.7\end{aligned}\)
Відповідь - 125,7.
Площа поверхні конуса дорівнює\(125.7 \text{ in}^{2}\).
Приклад\(\PageIndex{4}\)
Знайдіть площу поверхні конуса радіусом 5 футів і висотою нахилу 8 футів.
Рішення
По-перше, підставити те, що ви знаєте, у формулу площі поверхні.
\(\begin{aligned}SA&=\pi r^{2}+\pi rs \\ SA&=\pi (5)2+\pi (5)(8)\end{aligned}\)
Далі використовуйте алгебру для вирішення площі поверхні.
\(\begin{aligned}SA&=\pi (5)^{2}+\pi (5)(8) \\ SA&=\pi (25)+\pi (40) \\ SA&=78.5+125.7 \\ SA&=204.2\end{aligned}\)
Відповідь - 204.2.
Площа поверхні конуса дорівнює\(204.2\text{ ft}^2\).
Приклад\(\PageIndex{5}\)
Знайдіть площу поверхні конуса радіусом 3 дюйми і висотою нахилу 4,5 дюйма.
Рішення
По-перше, підставити те, що ви знаєте, у формулу площі поверхні.
\(\begin{aligned}SA&=\pi r^{2}+\pi rs \\ SA&=\pi (3)^{2}+\pi (3)(4.5)\end{aligned}\)
Далі використовуйте алгебру для вирішення площі поверхні.
\(\begin{aligned} SA&=\pi (3)^{2}+\pi (3)(4.5) \\ SA&=\pi (9)+\pi (13.5) \\ SA&=28.3+42.4 \\ SA&=70.7\end{aligned}\)
Відповідь - 70,7.
Площа поверхні конуса дорівнює\(70.7 \text{ in}^{2}\).
Рецензія
Дайте відповідь на запитання під кожною з наведених нижче діаграм
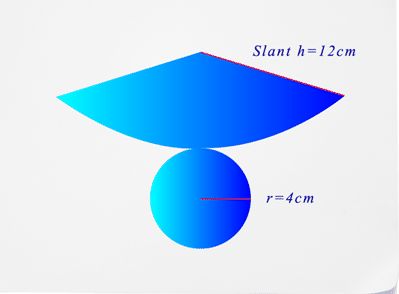
- Як називається фігура, представлена в цій мережі?
- Який діаметр у цієї цифри?
- Що таке похила висота фігури?
- Яка площа поверхні фігури?
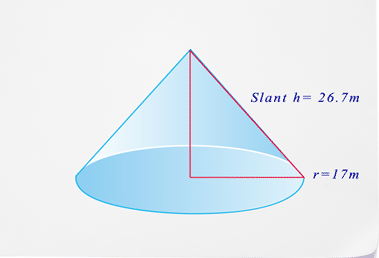
- Як називається ця фігура?
- Яка форма підстави?
- Який діаметр підстави?
- Яка площа поверхні цього малюнка?

- Як називається ця фігура?
- Яка форма підстави?
- Який діаметр підстави?
- Яка площа поверхні цього малюнка?
Знайдіть площу поверхні кожного конуса.
- \(r=4\text{ in}\),\(sh=5\text{ in}\)
- \(r=5 \text{ m}\),\(sh=7 \text{ m}\)
- \(r=3 \text{ cm}\),\(sh=6\text{ cm}\)
Огляд (Відповіді)
Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 8.9.
Ресурси
Лексика
| Термін | Визначення |
|---|---|
| Конус | Конус являє собою суцільну об'ємну фігуру з круглим підставою і однією вершиною. |
| Чистий | Сітка - це діаграма, яка показує «сплющений» вигляд твердого тіла. У сітці кожна грань і основа показані з усіма її розмірами. Сітка також може служити візерунком для побудови об'ємного твердого тіла. |
| Сектор | Сектор кола - це частина кола, що міститься між двома радіусами кола. Сектори можна вимірювати в градусах. |
| Площа поверхні | Площа поверхні - це загальна площа всіх поверхонь тривимірного об'єкта. |
| Висота нахилу | Висота нахилу - це висота бічної грані піраміди. |
Додаткові ресурси
Відео: Площа поверхні конуса - огляд
Практика: Площа поверхні конусів