9.20: Обсяг циліндрів
- Page ID
- 54457
Обсяг дорівнює площі верхньої або нижньої висоти.

Рамона підготувала великий горщик з фруктовими консервами, але вона закінчилася консервування банок, перш ніж вона консервувала всі консерви. Вона вийняла з шафи два контейнери для зберігання продуктів. Циліндричні контейнери мають розміри, наведені нижче. Не вистачає додаткового консерву для обох контейнерів, тому їй потрібен лише один з контейнерів, і він повинен бути з найбільшим об'ємом.

Як Рамона може використовувати ці розміри, щоб з'ясувати, який контейнер буде містити найбільше?
У цій концепції ви навчитеся використовувати формули для пошуку обсягу циліндрів.
Знаходження об'єму циліндрів
Обсяг - це кількість простору, що міститься в твердій фігурі. Що стосується циліндрів, ви можете думати про обсяг як ємність, або кількість рідини або речовини, яку вона може утримувати.
На відміну від призм, одиничні кубики не вписуються красиво в циліндр.

Отже, щоб точно розрахувати обсяг циліндра, потрібно використовувати формулу замість одиничних кубів.
Щоб розрахувати обсяг циліндра, почніть з розрахунку площі круглого підстави. Це дасть вам міру для кількості одиничних кубів, які можуть поміститися поперек дна циліндра. Висота циліндра покаже, наскільки високі кубики можна укладати всередину циліндра.
Ось формула знаходження обсягу циліндра.
\(V&= \pi r^{2}h\)
Давайте застосуємо цю формулу.

Радіус круглої основи - 2 дюйми. Висота циліндра - 7 дюймів. Якщо взяти обидві ці дані заходи і підставити їх у формулу, можна вирішити для обсягу циліндра.
\(\begin{aligned} V&= \pi r^{2} h \\ V&= (3.14)(2^{2})(7) \\ V&= (3.14)(4)(7) \\ V&= (3.14)(28) \\ V&= 87.92\text{ in}^{3}\end{aligned}\)
Обсяг циліндра дорівнює\(87.92\text{ in}^{3}\).
Приклад\(\PageIndex{1}\)
Раніше вам дали проблему про Рамону та її додаткові фруктові консерви.
Рамона має два контейнери для зберігання продуктів, але не впевнений, який буде тримати найбільше. Як Реймонд може використовувати ці розміри, щоб з'ясувати, які будуть утримувати найбільше?

Рішення
Почніть з контейнера зліва.
Спочатку зверніть увагу, що діаметр в два рази більше радіуса, тому розділіть діаметр на 2, щоб отримати радіус.
8\ розділити 2 = 4
Радіус дорівнює 4.
Далі підставляємо задану інформацію у формулу, а потім вирішуємо.
\(\begin{aligned}V&= \pi r^{2} h \\ V&= \pi (4)^{2} (16) \\ V&= \pi (16)(16) \\ V&= 256 \pi \\ V&= 803.84\text{ in}^{3}\end{aligned}\)
Перший контейнер вміщує 803,84 кубічних дюймів.
Далі розглянемо іншу ємність.
Спочатку зверніть увагу, що діаметр в два рази більше радіуса, тому розділіть діаметр на 2, щоб отримати радіус.
12\ розділити 2 = 6
Радіус дії 6.
Далі підставляємо задану інформацію у формулу, а потім вирішуємо.
\(\begin{aligned}V&= \pi r^{2} h \\ V&= \pi (6)^{2} (6) \\ V&= \pi (36)(6) \\ V&= 216 \pi \\ V&= 678.24\text{ in}^{3}\end{aligned}\)
Другий контейнер вміщує 678,24 кубічних дюймів.
Контейнер зліва має найбільший обсяг.
Приклад\(\PageIndex{2}\)
Використовуйте формулу знаходження обсягу циліндра, щоб відповісти на наступне питання.
Резервуар для води має радіус 50 футів і висоту 400 футів. Скільки кубічних футів води буде тримати бак, коли він заповнений?
Рішення
Спочатку підставляємо задану інформацію в формулу і вирішуємо.
\(\begin{aligned}V&= \pi r^{2}h \\ V&= \pi (502)(400) \\ V&= \pi (2,500)(400) \\ V&= 1,000,000 \pi \\ V&= 3,140,000\text{ in}^{3}\end{aligned}\)
Резервуар для води міститиме більше 3 мільйонів кубічних футів води!
Приклад\(\PageIndex{3}\)
Знайдіть обсяг циліндра.

Рішення
Спочатку підставляйте задану інформацію у формулу, а потім вирішіть.
\(\begin{aligned}V&= \pi r^{2} h \\ V&= \pi (1^{2})(8) \\ V&= \pi (1)(8) \\ V&= 8 \pi \\ V&= 25.12\text{ in}^{3}\end{aligned}\)
Відповідь - 25,12 кубічних дюймів.
Приклад\(\PageIndex{4}\)
Знайдіть обсяг циліндра.
d = 10\ текст {ft}\),\(h=12 \text{ ft}\)
Рішення
Спочатку зверніть увагу, що діаметр в два рази більше радіуса, тому розділіть діаметр на 2, щоб отримати радіус.
10\ розділити 2 = 5\)
Радіус дії дорівнює 5.
Далі підставляємо задану інформацію у формулу, а потім вирішуємо.
\(\begin{aligned}V&= \pi r^{2} h \\ V&= \pi (5)^{2} (12) \\ V&= \pi (25)(12) \\ V&= 300 \pi \\ V&= 942 \text{ ft}^{3}\end{aligned}\)
Відповідь - 942 кубічних футів.
Приклад\(\PageIndex{5}\)
Знайдіть обсяг циліндра.
\(r=6\text{ in}\),\(h=10\text{ in}\)
Рішення
Спочатку підставляйте задану інформацію у формулу, а потім вирішіть.
\(\begin{aligned}V&= \pi r^{2} h \\ V&= \pi (6)^{2}(10) \\ V&= \pi (36)(10) \\ V&= 360 \pi \\ V&= 1130.4\text{ in}^{3}\end{aligned}\)
Відповідь - 1130,4 кубічних дюймів.
Рецензія
Знайдіть обсяг кожного з наступних циліндрів.
- \(r=5\text{ in}\),\(h=8\text{ in}\)
- \(r=4\text{ in}\),\(h=7\text{ in}\)
- \(r=3 \text{ ft}\),\(h=5 \text{ ft}\)
- \(r=3 \text{ ft}\),\(h=8 \text{ ft}\)
- \(r=4 \text{ cm}\),\(h=9 \text{ cm}\)
-

Малюнок\(\PageIndex{7}\) -

Малюнок\(\PageIndex{8}\) -

Малюнок\(\PageIndex{9}\) -
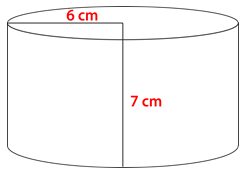
Малюнок\(\PageIndex{10}\) -
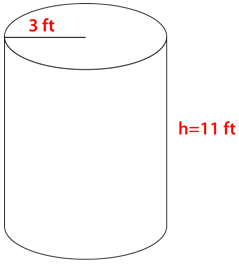
Малюнок\(\PageIndex{11}\) -

Малюнок\(\PageIndex{12}\) -

Малюнок\(\PageIndex{13}\) -

Малюнок\(\PageIndex{14}\) -
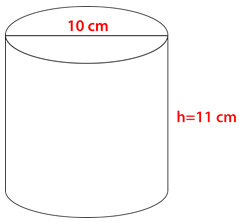
Малюнок\(\PageIndex{15}\) -

Малюнок\(\PageIndex{16}\)
Лексика
| Термін | Визначення |
|---|---|
| Циліндр | Циліндр - це суцільна фігура з двома паралельними конгруентними круговими основами. |
| Радіус | Радіус кола - це відстань від центру кола до краю кола. |
| Площа поверхні | Площа поверхні - це загальна площа всіх поверхонь тривимірного об'єкта. |
| Обсяг | Об'єм - це кількість простору всередині меж тривимірного об'єкта. |
Додаткові ресурси
Інтерактивний елемент
Відео: Об'єм твердої геометрії
Практика: Обсяг циліндрів
Реальний світ: чому плавають супертанкери?