Skip to main content
LibreTexts - Ukrayinska

9.19: Площа поверхні циліндрів

  1. Last updated
  2. Save as PDF
  • Page ID
    54515

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    \(SA=2 \pi r(h+r)\)

    F-D_E94776728DA4A5F701E29780C0E90D50C20F16326b40761136320d0c+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{1}\)

    Місіс Джонсон загортає циліндричну упаковку в коричневий папір, щоб вона могла надіслати його синові. Виходячи з показаних розмірів, скільки паперу їй знадобиться, щоб покрити упаковку?

    У цій концепції ви навчитеся знаходити площу поверхні циліндрів.

    Площа поверхні

    Циліндр має дві паралельні конгруентні круглі основи з вигнутим прямокутником як його сторона. Один із способів - використовувати сітку.

    Сітка - це двовимірна діаграма тривимірної фігури. Якби ви могли розгорнути циліндр (як балончик) так, щоб він був повністю плоским, у вас було б щось, що виглядає так.

    F-D_5388B3DF 7377CF14759ADC50208C0451C675DC59F62E337BF877F7CF+зображення_thumb_поштова листівка_крихітка+зображення_thumb_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{2}\)

    За допомогою сітки циліндра вам потрібно буде обчислити площу кожного кола і площу вигнутої сторони циліндра. Тоді ви можете додати ці значення разом, щоб знайти k.

    Формула\(A&= \pi r^{2}\) може бути використана для знаходження площі основи кола. Подивіться ще раз уважно на циліндр вище. Дві круглі грані конгруентні, тому вони повинні мати однаковий радіус і діаметр.

    Давайте розглянемо приклад.

    F-D_83DE5292A123C4EA44BBC29F7D93C9556611784990F854C456EE+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{3}\)

    Спочатку розрахуйте площу кругових підстав.

    \(\begin{aligned} A&= \pi r^{2}\\ A&= \pi (4)^{2} \\ A&= \pi (16) \\ A&=50.3\end{aligned}\)

    Далі знайдіть довжину сторони циліндра. Ви знаєте, що ширина становить 8 см, але довжина не показана. Циліндр був розгорнутий, щоб утворилася сітка. Тому окружність кола буде довжиною сторони.

    \(\begin{aligned}C&=2 \pi r \\ C&=2 \pi \times 4 \\ C&=25.1\end{aligned}\)

    Потім розрахуйте площу бортика.

    \(\begin{aligned}A&=l\times w \\ A&=25.1\times 8 \\ A&=200.8\end{aligned}\)

    Потім знайдіть площу поверхні циліндра, додавши бічну область до верхньої та нижньої області.

    \(\begin{aligned}SA&=bottom+top+side \\ SA&=50.3+50.3+200.8 \\ SA&=301.4\end{aligned}\)

    Відповідь - 301.4.

    Площа поверхні циліндра дорівнює\(301.4 \text{ cm}^{2}\).

    Поклавши це все воєдино, можна скористатися наступною формулою, щоб знайти площу поверхні циліндра:

    \(SA=2 \pi r^{2}+2 \pi rh\)

    Формула\(2 \pi r^{2}\) представляє площу верхнього і нижнього кіл циліндра. The\(2 \pi r h\) являє собою периметр (\(2 \pi r\)), помножений на висоту,\(h\).

    Давайте розглянемо приклад.

    Яка площа поверхні малюнка нижче?

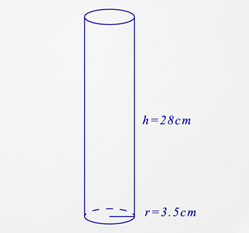
    F-D_B9 FAD338ДК6Б517ФД52Ф686CB87FF42148d8D8139811AA2F113C2B4A4A+зображення_thumb_поштова листівка_крихітка_зображення_великий палецька_листівка_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    По-перше, підставити те, що ви знаєте, у формулу площі поверхні.

    \(\begin{aligned}SA&=2 \pi r^{2}+2 \pi r h \\ SA&=2 \pi (3.5)^{2}+2 \pi (3.5)(28)\end{aligned}\)

    Далі слід розрахувати площу поверхні.

    \(\begin{aligned}SA&=2 \pi (3.5)^{2}+2 \pi (3.5)(28) \\ SA&=2 \pi (12.25)+2 \pi (98) \\ SA&=76.97+615.75 \\ SA&=692.72\end{aligned}\)

    Відповідь 692.72.

    Площа поверхні циліндра дорівнює\(692.7 \text{ cm}^{2}\).

    Іноді у вас може бути циліндр, який був розрізаний. Це називається усіченим циліндром. Тут ви бачите лише ділянку циліндра, і вам потрібно буде з'ясувати площу поверхні того, що ви бачите.


    F-D_88117a24d863FE7902E7CB78CFFFB7255F60C9B84617FF6E23C4341B1+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{5}\)

    Приклад\(\PageIndex{1}\)

    Раніше вам поставили проблему з циліндричним обгортанням місіс Джонсон.

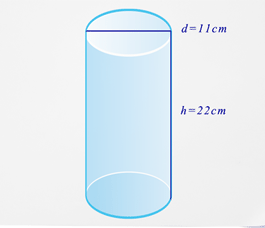
    F-D_825C1834C1966c53c75299D3585E38664A5D6A88BD0F2B65859C30+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{6}\)

    Рішення

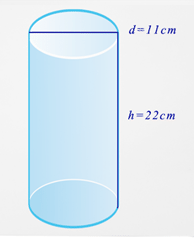
    Для початку потрібно знайти радіус. Пам'ятайте, радіус дорівнює половині міри діаметра.

    \(\begin{aligned}r&=\dfrac{d}{2} \\ r&=\dfrac{11}{2} \\ r&=5.5v\end{aligned}\)

    Далі підставте те, що ви знаєте, у формулу площі поверхні.

    \(\begin{aligned}SA&=2 \pi r^{2}+2 \pi rh \\ SA&=2 \pi (5.5)^{2}+2 \pi (5.5)(22)\end{aligned}\)

    Потім розрахуйте площу поверхні.

    \(\begin{aligned}SA&=2 \pi (5.5)^{2}+2 \pi (5.5)(22) \\ SA&=2 \pi (30.25)+2 \pi (121) \\ SA&=190.1+760.3 \\ SA&=950.4\end{aligned}\)

    Відповідь - 950,4.

    Місіс Джонсон потребує\(950.4 \: cm^{2}\) коричневого паперу, щоб обернути її посилку.

    Приклад\(\PageIndex{2}\)

    Яка площа поверхні малюнка нижче?


    F-D_8B9EF10435CCA133B655AF91B0402E96BF73F279E7393BDEAE341+зображення_thumb_поштова листівка_крихітка+зображення_thumb_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{7}\)

    Рішення

    Для початку потрібно знайти радіус. Пам'ятайте, що радіус дорівнює половині міри діаметра.

    \(\begin{aligned}r&=\dfrac{d}{2} \\ r&=\dfrac{13}{2} \\ r&=6.5\end{aligned}\)

    Далі підставте те, що ви знаєте, у формулу площі поверхні.

    \(\begin{aligned}SA&=2 \pi r^{2}+2 \pi rh \\ SA&=2 \pi (6.5)^{2}+2 \pi (6.5)(11)\end{aligned}\)

    Потім розрахуйте площу поверхні.

    \(\begin{aligned}SA&=2 \pi (6.5)^{2}+2 \pi (6.5)(11) \\ SA&=2 \pi (42.25)+2 \pi (71.5) \\ SA&=265.5+449.2 \\ SA&=714.7\end{aligned}\)

    Відповідь - 714,7.

    Площа поверхні циліндра дорівнює\ (714.7\: ft^ {2}.

    Приклад\(\PageIndex{3}\)

    Знайдіть площу поверхні циліндра радіусом 6 дюймів і висотою 5 дюймів.

    Рішення

    По-перше, підставити те, що ви знаєте, у формулу площі поверхні.

    \(\begin{aligned}SA&=2 \pi r^{2}+2 \pi rh \\ SA&=2 \pi (6)^{2}+2 \pi (6)(5)\end{aligned}\)

    Далі слід розрахувати площу поверхні.

    \(\begin{aligned} SA&=2 \pi (6)^{2}+2 \pi (6)(5) \ SA&=2 \pi (36)+2 \pi (30) \\ SA&=226.2+188.5 \\ SA&=414.7\end{aligned}\)

    Відповідь - 414,7.

    Площа поверхні циліндра дорівнює\(414.7 \: in^{2}\).

    Приклад\(\PageIndex{4}\)

    Знайдіть площу поверхні циліндра радіусом 4 см і висотою 12 см.

    Рішення

    По-перше, підставити те, що ви знаєте, у формулу площі поверхні.

    \(SA&=2 \pi r^{2}+2 \pi rh \\ SA&=2 \pi (4)^{2}+2 \pi (4)(12)\end{aligned}\)

    Далі слід розрахувати площу поверхні.

    \(\begin{aligned} SA&=2 \pi (4)^{2}+2 \pi (4)(12) \\ SA&=2 \pi (16)+2 \pi (48) \\ SA&=100.5+301.6 \\ SA&=402.1\end{aligned}\)

    Відповідь - 402.1.

    Площа поверхні циліндра дорівнює\(402.1 \: cm^{2}\).

    Приклад\(\PageIndex{5}\)

    Знайдіть площу поверхні циліндра діаметром 10 метрів і висотою 15 метрів.

    Рішення

    Для початку потрібно знайти радіус. Пам'ятайте, що радіус дорівнює половині міри діаметра.

    \(\begin{aligned} r&=\dfrac{d}{2} \\ r&=\dfrac{10}{2} \\ r&=5\end{aligned}\)

    Далі підставте те, що ви знаєте, у формулу площі поверхні.

    \(\begin{aligned} SA&=2 \pi r^{2}+2 \pi r h \\ SA&=2 \pi (5)^{2}+2 \pi (5)(15)\end{aligned}\)

    Потім розрахуйте площу поверхні.

    \(\begin{aligned}SA&=2 \pi (5)^{2}+2 \pi (5)(15) \\ SA&=2 \pi (25)+2 \pi (75) \\ SA&=157.1+471.2 \\ SA&=628.3\end{aligned}\)

    Відповідь - 628.3.

    Площа поверхні циліндра дорівнює\(628.3 \: m^{2}\).

    Рецензія

    Використовуйте діаграми, щоб відповісти на запитання під кожною з них.

    F-D_5FAB4D988C4232D399759E99E073cd0F095347f401348d8C03592A12+зображення_тум_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{8}\)
    1. Як називається ця фігура?
    2. Яка форма підстави цієї фігури?
    3. Скільки існує підстав?
    4. Яка площа поверхні цього малюнка?
    5. Яке вимірювання потрібно радіус або діаметр?
    F-D_54AB8B572D5A2B758227900E00E487DD5915F16360F90672846F973+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{9}\)
    1. Як називається ця фігура?
    2. Яке вимірювання дається радіус або діаметр?
    3. Яка площа поверхні фігури?

    Використовуйте те, що ви навчилися, щоб відповісти на кожне питання.

    1. Циліндричний резервуар для води має довжину 35 і 10 футів в поперечнику. Скільки листового металу виготовлений бак?
    2. Ви використовували площу або площу поверхні для вирішення цієї проблеми?
    3. Правда чи брехня. Дізнатися площу поверхні можна тільки в тому випадку, якщо ви знаєте обсяг.
    4. Правда чи брехня. Площа поверхні і об'єм вимірюють одне і те ж.
    5. Правда чи брехня. Площа поверхні вимірює зовнішню сторону циліндра.
    6. Правда чи брехня. Вам потрібен радіус, щоб знайти площу поверхні циліндра.
    7. Правда чи брехня. Радіус дорівнює половині діаметра.

    Огляд (Відповіді)

    Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 8.7.

    Лексика

    Термін Визначення
    Циліндр Циліндр - це суцільна фігура з двома паралельними конгруентними круговими основами.
    Чистий Сітка - це діаграма, яка показує «сплющений» вигляд твердого тіла. У сітці кожна грань і основа показані з усіма її розмірами. Сітка також може служити візерунком для побудови об'ємного твердого тіла.
    Призма Призма - це тривимірний об'єкт з двома конгруентними паралельними основами, які є багатокутниками.
    Площа поверхні Площа поверхні - це загальна площа всіх поверхонь тривимірного об'єкта.
    Тривимірні Фігура, намальована в трьох вимірах, малюється з використанням довжини, ширини і висоти або глибини.
    усічений циліндр Циліндр, який частково вирізається з повного циліндра.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Об'єм циліндра і площа поверхні

    Практика: Площа поверхні циліндрів

    Реальний світ: чому плавають супертанкери?