3.11: Будівництво лінії

Last updated
Save as PDF

Page ID: 54560

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Створіть лінії, які не перетинаються або не перетинаються під кутом 90 градусів за допомогою циркуля і прямолінійного краю.

Паралельні та перпендикулярні

Конструкції - це покрокові процеси, що використовуються для створення точних геометричних фігур. Для створення конструкції своїми руками є кілька інструментів, які можна використовувати:

Компас: Пристрій, що дозволяє створити коло із заданим радіусом. Компаси можуть не тільки допомогти вам створити кола, але також вони можуть допомогти вам копіювати відстані.
Straightedge: Все, що дозволяє виробляти пряму лінію. Прямолінійний край не повинен вміти вимірювати відстані. Індексна картка добре працює як прямий край. Ви також можете використовувати лінійку як прямий край, якщо ви використовуєте її лише для малювання прямих ліній, а не для вимірювання.
Папір: Коли геометрична фігура знаходиться на аркуші паперу, сам папір можна скласти, щоб побудувати нові лінії.

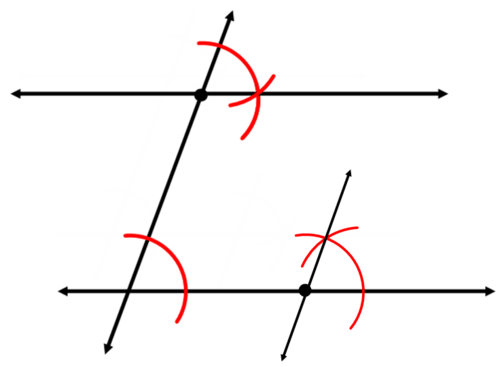
Для побудови паралельних ліній пам'ятайте, що якщо відповідні кути конгруентні, то лінії паралельні. Це означає, що якщо ви можете скопіювати кут для створення конгруентних відповідних кутів, ви можете створити паралельні лінії. Це буде досліджено на прикладі А.

Щоб побудувати перпендикулярні лінії, пам'ятайте, що ви вже знаєте, як побудувати перпендикулярну бісектрису. Цей метод можна використовувати для побудови лінії, перпендикулярної іншій лінії через будь-яку задану точку.

Давайте розглянемо приклад проблеми.

Використовуйте свій straightedge, щоб намалювати лінію і точку, як показано нижче. Потім побудуйте лінію через точку, яка паралельна вихідній лінії.

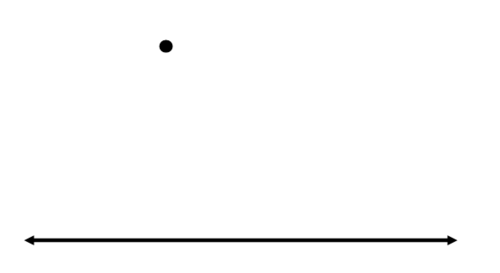
Почніть з використання вашого straightedge, щоб провести лінію через точку, яка перетинає вихідну лінію. Це стане поперечним після того, як ви побудували паралельну лінію.

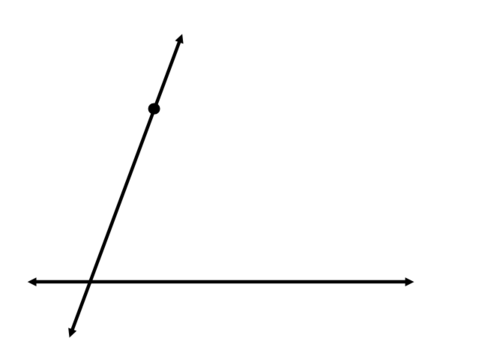
Тепер ваша мета полягає в тому, щоб скопіювати один з чотирьох кутів, створених на перетині двох ліній. Намалюйте дугу через кут, який ви будете копіювати:

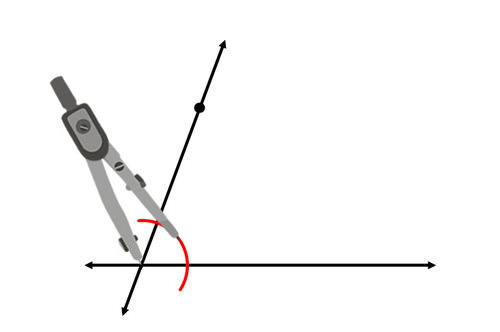
Намалюйте дугу з однаковим радіусом у відповідному місці, з початковою точкою в якості вершини.

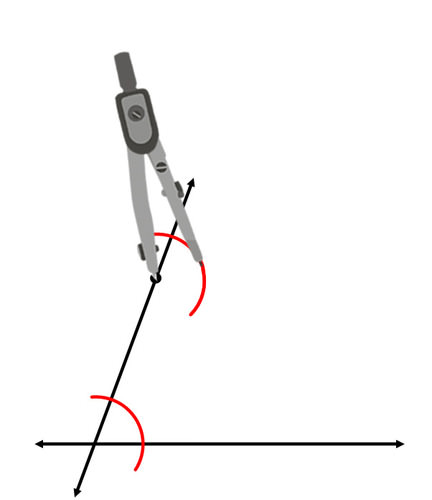
Продовжуйте копіювати кут, виміряючи його ширину та відзначивши правильну ширину для нового кута.

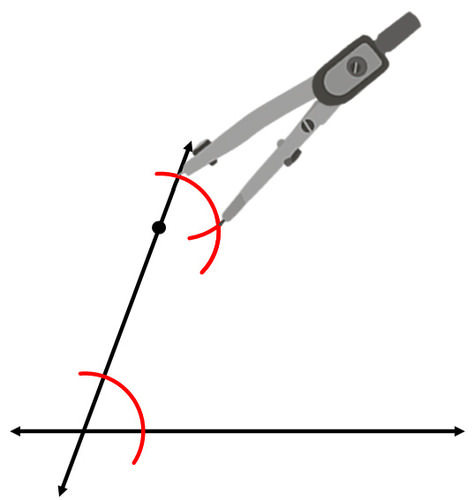
Використовуйте свій straightedge, щоб побудувати паралельну лінію.

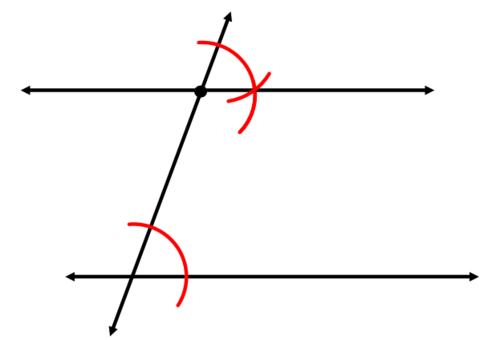
Тепер давайте пояснимо, чому два рядки в другому прикладі вище паралельні.

Якщо відповідні кути конгруентні, то лінії паралельні. У другому прикладі вище було скопійовано кут. Це створило конгруентні кути. Оскільки скопійований кут ставився в місце розташування відповідного кута, конструкція створювала відповідні кути. Тому дві лінії повинні бути паралельними.

Використовуйте свій straightedge, щоб намалювати лінію і точку, як показано нижче. Потім побудуйте лінію через точку, яка перпендикулярна вихідній лінії.

Ви вже знаєте, як побудувати перпендикулярну бісектрису відрізка. Спочатку знайдіть відрізок, перпендикулярна бісектриса якого буде проходити через задану точку. Намалюйте часткове коло по центру в точці, яка проходить через задану пряму два рази.

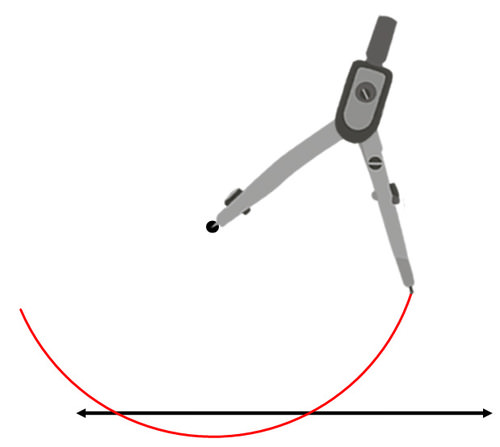
Відрізок, який з'єднує дві точки перетину, - це відрізок, для якого ви побудуєте перпендикулярну бісектрису:

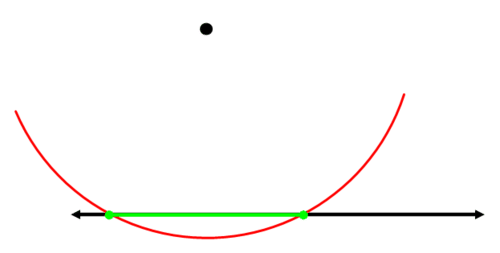
Побудувати перпендикулярну бісектрису зеленого відрізка:

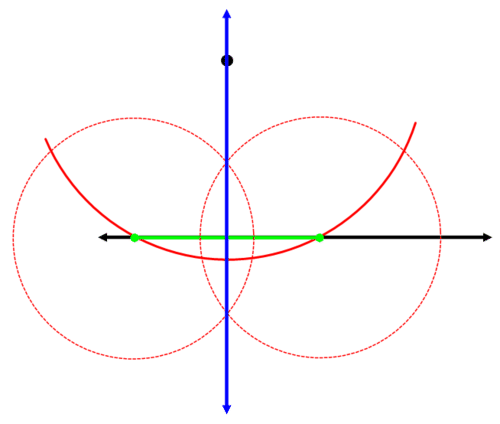
Синя лінія перпендикулярна вихідній лінії і проходить через вихідну точку.

Приклад\(\PageIndex{1}\)

Побудуйте трикутник за допомогою прямогокраю. Тепер побудуйте три висоти трикутника, щоб знайти ортоцентр трикутника.

Рішення

Почніть з загального трикутника:

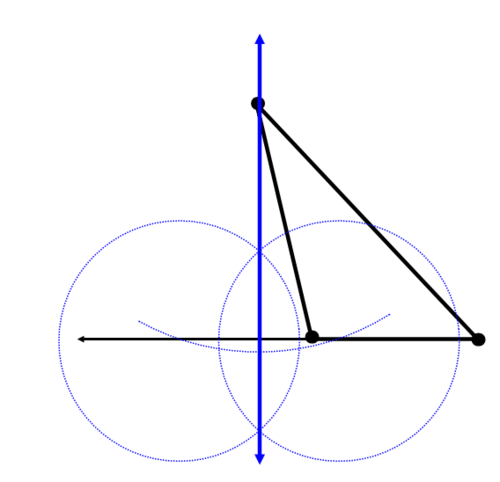
Побудуйте перпендикулярну лінію через кожну сторону, яка проходить через протилежну вершину. Можливо, доведеться подовжити довжину деяких сторін. Блакитна лінія нижче - перша висота:

Червона лінія - друга висота:

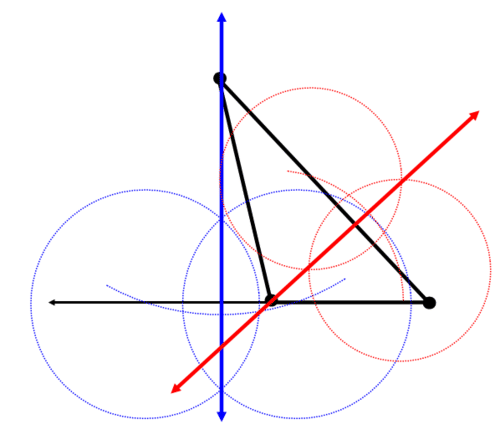
Зелена лінія - третя висота:

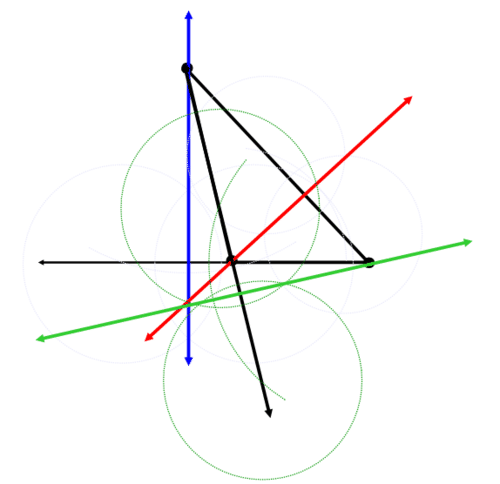
Синій, червоний і зелений лінії перетинаються в точці. Ця точка є ортоцентром.

Приклад\(\PageIndex{2}\)

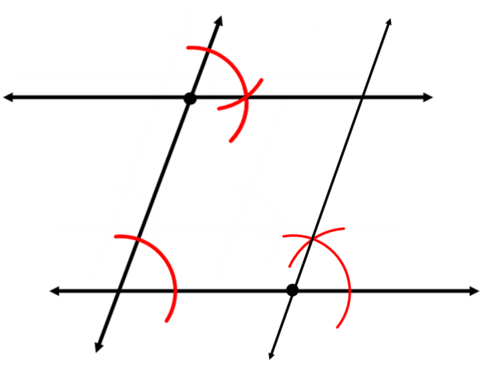
Намалюйте відрізок лінії. Побудуйте лінію, паралельну відрізку лінії.

Рішення

Приклад\(\PageIndex{3}\)

Розширте свою конструкцію з Прикладу 2, щоб побудувати паралелограм.

Рішення

Розширте свою конструкцію з Прикладу 2, щоб побудувати паралелограм.

Продовжити нову паралельну лінію. Утворений чотирикутник являє собою паралелограм.

Приклад\(\PageIndex{4}\)

Як ви можете бути впевнені, що ваш чотирикутник з Прикладу 3 - це паралелограм?

Рішення

Паралелограм - це чотирикутник з двома парами паралельних сторін. Конструкція створювала дві пари паралельних ліній, тому чотирикутник повинен бути паралелограмом.

Рецензія

Намалюйте відрізок лінії і точку.

1. Побудуйте лінію, перпендикулярну відрізку лінії, яка проходить через точку.

2. Побудуйте лінію, паралельну відрізку лінії, яка проходить через точку.

3. Розширте свою конструкцію, щоб побудувати прямокутник. Поясніть, що ви зробили, щоб побудувати прямокутник.

Намалюйте ще один відрізок лінії і точку.

4. Побудуйте лінію, паралельну відрізку лінії, яка проходить через точку.

5. Розширте свою конструкцію, щоб побудувати паралелограм. Поясніть, що ви зробили для побудови паралелограма.

За допомогою прямолінійного краю намалюйте трикутник.

6. Побудувати висоти трикутника.

7. Знайти точку перетину висот. Що це за сенс?

8. Чи була ваша точка перетину всередині або зовні трикутника? Якщо він був всередині, створіть новий трикутник, який призведе до того, що точка перетину виявиться поза трикутником. Якщо він був зовні, створіть новий трикутник, який призведе до того, що точка перетину виявиться всередині трикутника.

Намалюйте ще один відрізок лінії і точку.

9. Побудуйте лінію, паралельну відрізку лінії, яка проходить через точку.

10. Розширте свою конструкцію, щоб побудувати трапецію. Поясніть, що ви зробили для побудови трапеції.

Намалюйте ще один відрізок лінії і точку.

11. Побудуйте лінію, перпендикулярну відрізку лінії, яка проходить через точку.

12. Розширте свою конструкцію, щоб побудувати квадрат. Поясніть, що ви зробили, щоб побудувати квадрат.

13. Обґрунтуйте, чому фігура, яку ви створили в #12, повинна бути квадратною.

14. Поясніть, чому метод побудови паралельних ліній передбачає копіювання кута.

15. Поясніть, чому метод побудови перпендикулярних ліній спирається на метод побудови перпендикулярної бісектриси.

Лексика

Термін	Визначення
висота	Висота трикутника - це відрізок лінії від вершини і перпендикулярний протилежній стороні. Його ще називають висотою трикутника.
Відповідні кути	Відповідні кути - це два кути, які знаходяться в одному положенні щодо поперечного, але на різних лініях.
перпендикулярні лінії	Перпендикулярні лінії - це лінії, які перетинаються під кутом 90.
Вершина	Вершина - це точка перетину ліній або променів, які утворюють кут.
Ортоцентр	Ортоцентр - це точка, в якій зустрічаються три висоти трикутника.