Skip to main content
LibreTexts - Ukrayinska

1.1: Геометрія Терміни

  1. Last updated
  2. Save as PDF
  • Page ID
    54987

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Визначте та використовуйте терміни, включаючи точки, лінії, площини, простір та постулати.

    Геометричні визначення

    Точка - це точне місце розташування в просторі. Він описує місце розташування, але не має розміру. Приклади наведені нижче:

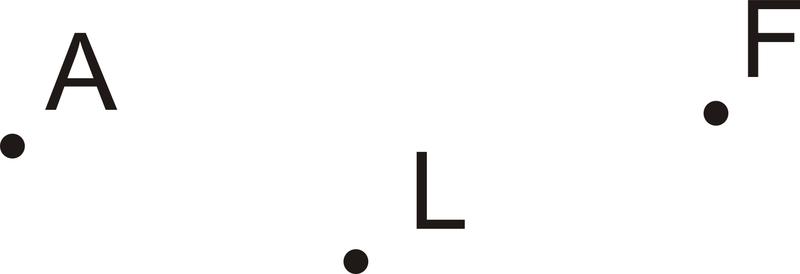
    Ф-д_Е95С300933 АБ3123Ф04393792Ф130ФА63ЕД 0Е9Ф6Д 2029Д9СБ3Д18+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)
    Таблиця 1.1.1
    Позначте це Скажи це
    \(A\) точка\(A\)

    Лінія - це нескінченно багато точок, які вічно тягнуться в обидві сторони. Лінії мають напрямок і розташування і завжди прямі.

    Ф-Д_Ф38Ф5С2650Е467 ДБ31А80130427С7Д3С0Д6ДД23Д5КС0 А0CF93E43+зображення_крихіткий+зображення_крихіткий.PNG

    Малюнок\(\PageIndex{2}\)

    Table 1.1.2
    Label It Say It
    line \(g\) line \(g\)
    \(\overleftrightarrow{PQ}\) line \(PQ\)

    A plane is a flat surface that contains infinitely many intersecting lines that extend forever in all directions. Think of a plane as a huge sheet of paper with no thickness that goes on forever.

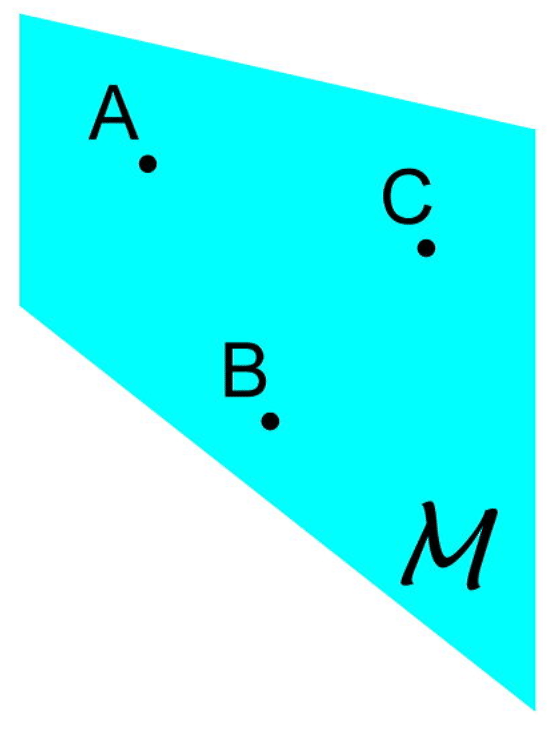
    f-d_ca0c46e10ec92e72a101656a657ed651198bb25050cd90b25378f230+IMAGE_TINY+IMAGE_TINY.png
    Figure \(\PageIndex{3}\)
    Table 1.1.3
    Label It Say It
    Plane \(M\) Plane \(M\)
    Plane \(ABC\) Plane \(ABC\)

    We can use point, line, and plane to define new terms.

    Space is the set of all points extending in three dimensions. Think back to the plane. It extended in two dimensions, what we think of as up/down and left/right. If we add a third dimension, one that is perpendicular to the other two, we arrive at three-dimensional space.

    Points that lie on the same line are collinear. \(P\),\(Q\),\(R\),\(S\), and \(T\) are collinear because they are all on line \(w\). If a point U were located above or below line w, it would be non-collinear.

    f-d_87d4ba3712d96c4a9ba243440f90b173948bc745bc9271b36a8adf89+IMAGE_TINY+IMAGE_TINY.png
    Figure \(\PageIndex{4}\)

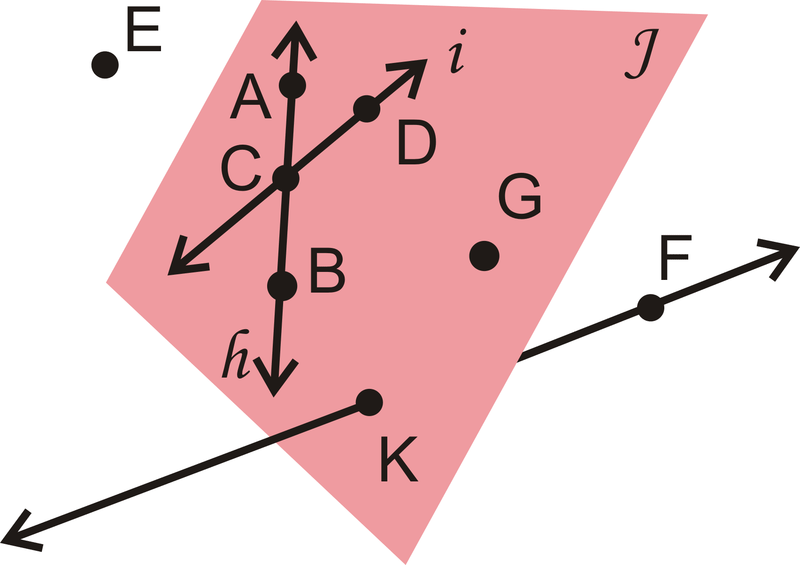
    Points and/or lines within the same plane are coplanar. Lines h and i, and points \(A\),\(B\),\(C\),\(D\),\(G\), and \(K\) are coplanar in Plane \(J\). Line \(\overleftrightarrow{KF}\) and point \(E\) are non-coplanar with Plane \(J\).

    f-d_07649d2a898922dcc53ce196c55c0834882c127ebd6c9cf228b2f34f+IMAGE_TINY+IMAGE_TINY.png
    Figure \(\PageIndex{5}\)

    An endpoint is a point at the end of a line segment. A line segment is a portion of a line with two endpoints. Or, it is a finite part of a line that stops at both ends. Line segments are labeled by their endpoints. Order does not matter.

    f-d_9f178f97b87b417d128cba0bd169f998766226db3e604e3aeca17edc+IMAGE_TINY+IMAGE_TINY.png
    Figure \(\PageIndex{6}\)
    Table 1.1.4
    Label It Say It
    \(\overline{AB}\) Segment \(AB\)
    \(\overline{BA}\) Segment \(BA\)

    A ray is a part of a line. It begins with an endpoint and extends forever away from the endpoint in one direction, perfectly straight. A ray is labeled by its endpoint and one other point on the ray. For rays, order does matter. When labeling, put the endpoint under the side WITHOUT the arrow.

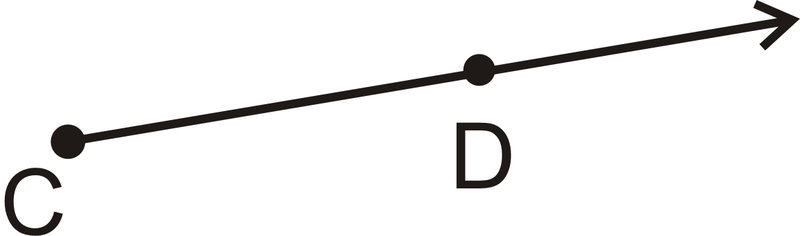
    f-d_f845b6a6ac79d3d1186c6813d305e0ca827a49dd577247ecbea54a79+IMAGE_TINY+IMAGE_TINY.png
    Figure \(\PageIndex{7}\)
    Table 1.1.5
    Label It Say It
    \(\overrightarrow{CD}\) Ray \(CD\)
    \(\overleftarrow{DC}\) Ray \(CD\)

    An intersection is a point or set of points where lines, planes, segments, or rays overlap.

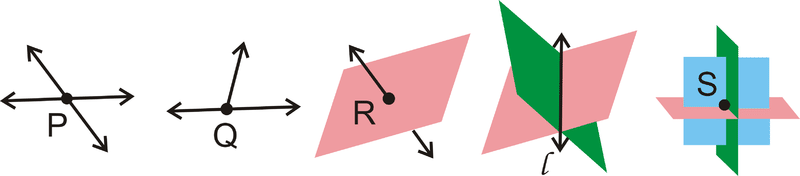
    f-d_22164a3d57328068dfcb6dd15ac5ff616fc578634687981d138b3fbb+IMAGE_TINY+IMAGE_TINY.png
    Figure \(\PageIndex{8}\)

    Postulates

    A postulate is a basic rule of geometry. Postulates are assumed to be true (rather than proven), much like definitions. The following is a list of some basic postulates.

    Postulate #1: Given any two distinct points, there is exactly one (straight) line containing those two points.

    f-d_5d486e865b0dd1b28c166f3dd81e3e328f111761ffb02a3e05078fbf+IMAGE_TINY+IMAGE_TINY.png
    Figure \(\PageIndex{9}\)

    Postulate #2: Given any three non-collinear points, there is exactly one plane containing those three points.

    f-d_0121737b10d9eaaf030efde9d153816bccfd2a026fe9c382911595fe+IMAGE_TINY+IMAGE_TINY.png
    Figure \(\PageIndex{10}\)

    Postulate #3: If a line and a plane share two points, then the entire line lies within the plane.

    f-d_a5c47fa34c5cdca34d148d3aefcdc5ee6faf1a7285905d23aef99276+IMAGE_TINY+IMAGE_TINY.png
    Figure \(\PageIndex{11}\)

    Postulate #4: If two distinct lines intersect, the intersection will be one point.

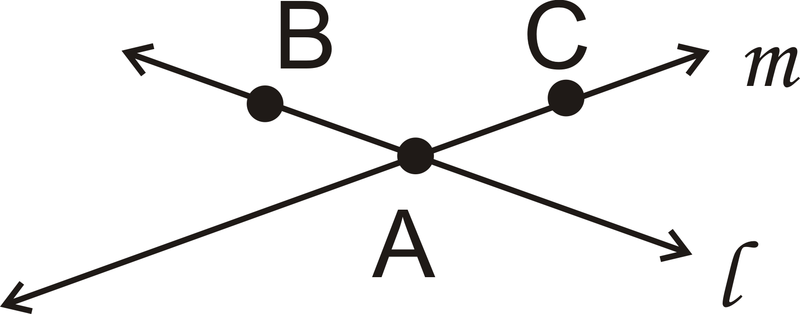
    f-d_0f48448ed151d2af85725df0734be9a44e96f20d51ab617b48ef5387+IMAGE_TINY+IMAGE_TINY.png
    Figure \(\PageIndex{12}\)

    Lines \(I\) and \(m\) intersect at point \(A\).

    Postulate #5: If two distinct planes intersect, the intersection will be a line.

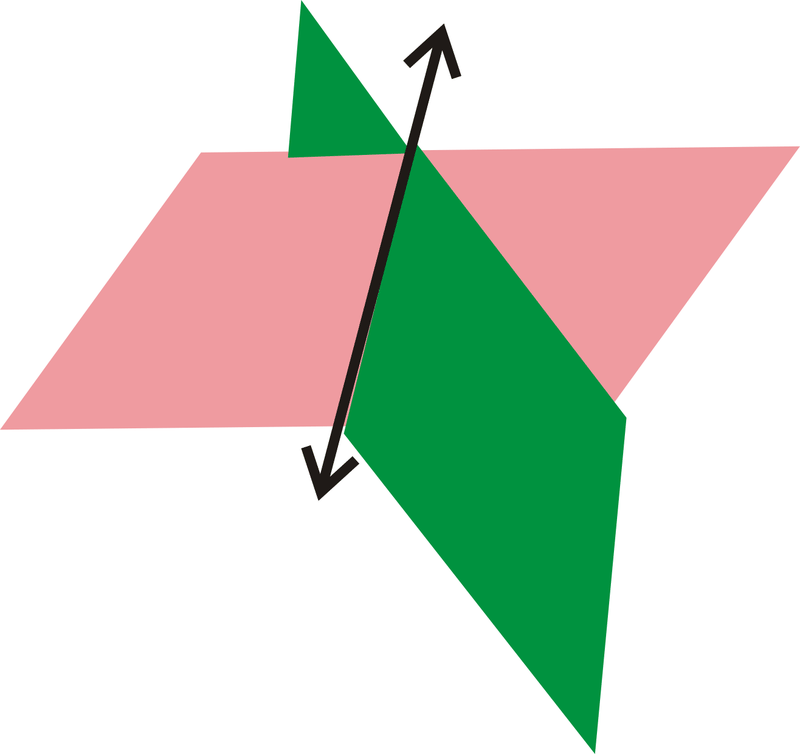
    f-d_17682b1829beda5ccf884ee2df3cb280c3b8f0de51935adb0e92ed57+IMAGE_TINY+IMAGE_TINY.png

    Figure \(\PageIndex{13}\)

    When making geometric drawings, be sure to be clear and label all points and lines.

    What if you were given a picture of a figure or object, like a map with cities and roads marked on it? How could you explain that picture geometrically?

    Example \(\PageIndex{1}\)

    What best describes San Diego, California on a globe: point, line, or plane?

    Solution

    A city is usually labeled with a dot, or point, on a globe.

    Example \(\PageIndex{2}\)

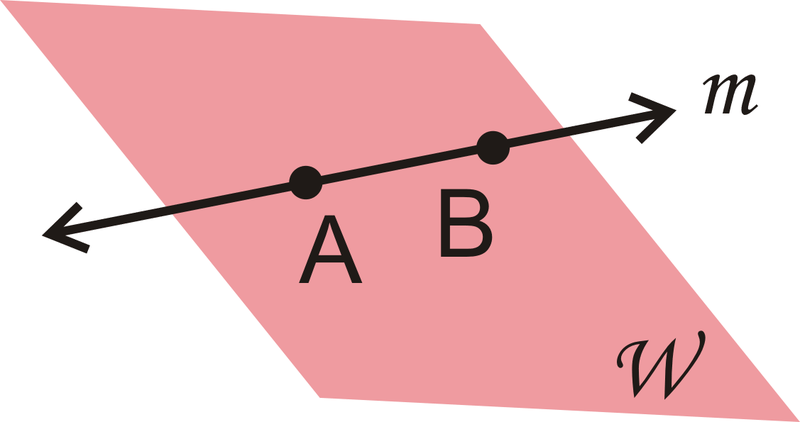
    Use the picture below to answer these questions.

    f-d_07649d2a898922dcc53ce196c55c0834882c127ebd6c9cf228b2f34f+IMAGE_TINY+IMAGE_TINY.png

    Малюнок\(\PageIndex{14}\)

    1. Перерахуйте інший спосіб позначення Plane\(J\).
    2. Перерахуйте інший спосіб позначення рядка\(h\).
    3. Чи є\(K\) і\(F\) колінеарні?
    4. Є\(E\),\(B\) і\(F\) копланарний?

    Рішення

    1. \(BDG\)Літак - одна з можливостей. Будь-яка комбінація трьох копланарних точок, які не є колінеарними, була б правильною.
    2. \(\overleftrightarrow{AB}\). Будь-яка комбінація з двох букв\(A\)\(B\), або також\(C\) буде правильною.
    3. Так, вони обидва лежать на\(\overleftrightarrow{KF}\).
    4. Так, хоча\(E\) це не в площині\(J\), будь-які три точки роблять окрему площину. Тому три точки створюють площину\(EBF\).

    Приклад\(\PageIndex{3}\)

    Що найкраще описує пряму дорогу, яка починається в одному місті і зупиняється в другому місті: промінь, лінія, відрізок або літак?

    Рішення

    Пряма дорога з'єднує два міста, які схожі на кінцеві точки. Кращий термін - сегмент.

    Приклад\(\PageIndex{4}\)

    Дайте відповідь на наступні питання щодо картини.

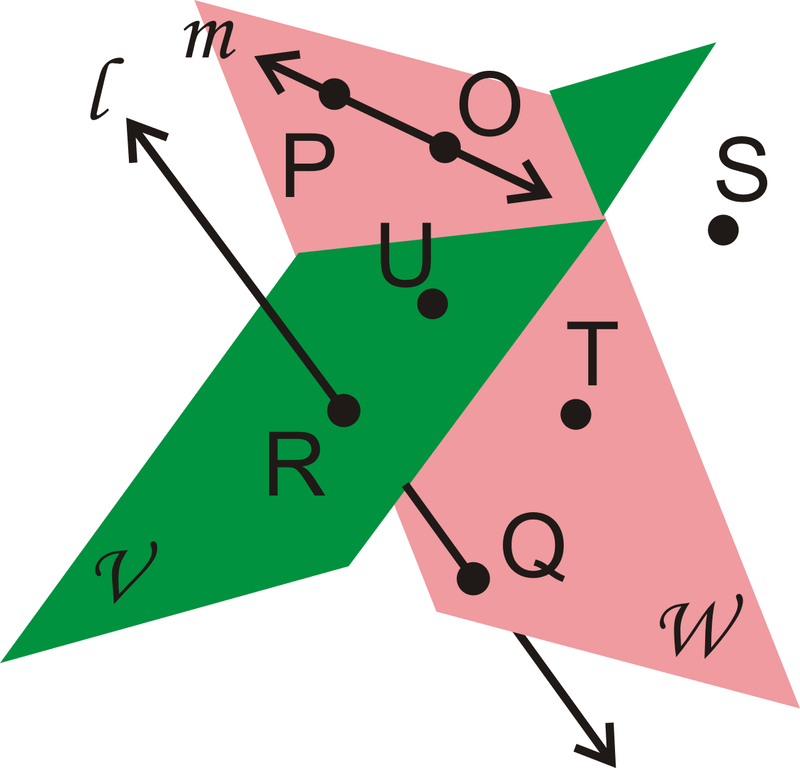
    Ф-Д_ДД26Ф72КД 908BCA3Ф84Ф83628БАФ 23001FF7BA715543521БФ 59D9977+зображення_крихіткий+зображення_крихіткий_png
    Малюнок\(\PageIndex{15}\)
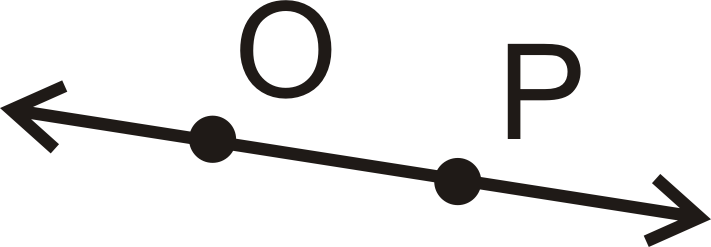
    1. Чи є лінія\(l\) coplanar з Plane\(V\),\(W\) Plane, обидва, або ні?
    2. Чи є\(R\) і\(Q\) колінеарні?
    3. Яка точка не належить ні Площині V, ні Площині\(W\)?
    4. Перерахуйте три точки в Площині\(W\).

    Рішення

    1. Ні
    2. Так
    3. S
    4. Будь-яке поєднання\(P\)\(O\),\(T\), і\(Q\) буде працювати.

    Приклад\(\PageIndex{5}\)

    Намалюйте та позначте фігуру, що відповідає наступному опису: Лінія\(\overleftrightarrow{AB}\) та промінь\(\overrightarrow{CD}\) перетинаються в точці\ (C)\. Потім перемалюйте так, щоб фігура виглядала інакше, але все ще відповідала опису.

    Рішення

    Ні положення A, ні B на лінії, ні напрямок, який\(\overrightarrow{CD}\) вказує, не мають значення.

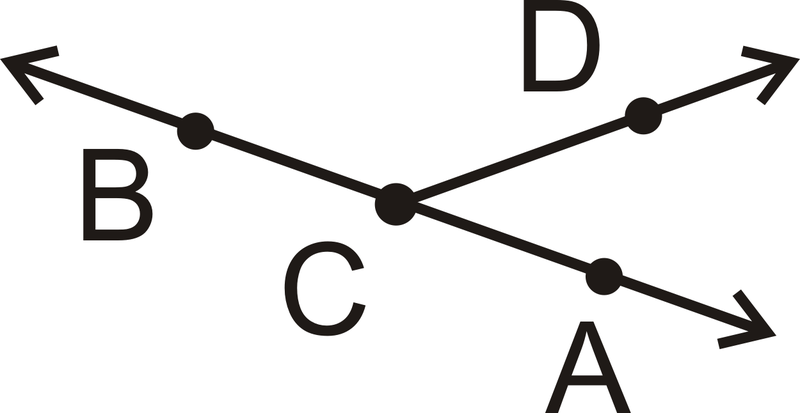
    F-D_67a758A944E5980A65Ф9C98119A30Ф1А0Б8749АФ7 BE5DE573D29B66+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{16}\)

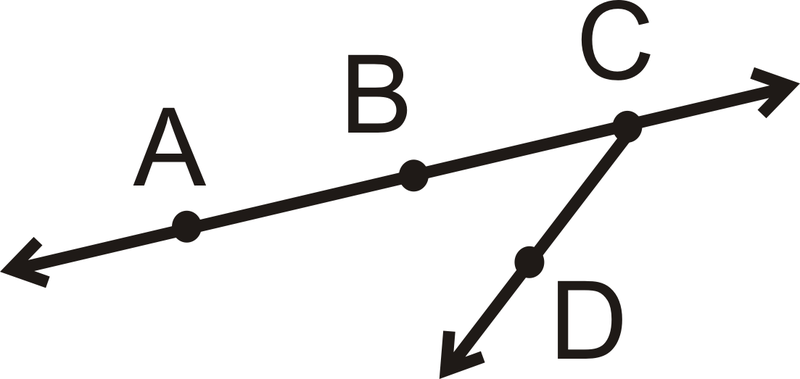
    Для другої частини це один із способів намалювати схему по-іншому:

    F-д_94Ф1А9 Деб 2Ф550031 ФК 25553Д1А79А784Ф220Д5Д93А4Е98Д8207С4ДБ+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{17}\)

    Рецензія

    Для питань 1-5 намалюйте та позначте фігуру, яка відповідає опису.

    1. \(\overrightarrow{CD}\)перетинається\(\overline{AB}\) і площина,\(P\) що містить\(\overline{AB}\), але ні\(\overrightarrow{CD}\).
    2. Три колінеарні точки\(A\)\(B\), і\(C\). \(B\)також колінеарний з точками\(D\) і\(E\).
    3. \(\overrightarrow{XY}\),\(\overrightarrow{XZ}\), І\(\overrightarrow{XW}\), такі, що\(\overrightarrow{XY}\) і\(\overrightarrow{XZ}\) є копланарними, але\(\overrightarrow{XW}\) є некопланарними з обома іншими променями.
    4. Дві пересічні площини,\(P\) причому\(Q\), з\(\overline{GH}\), де\(G\) знаходиться в площині\(P\) і\(H\) знаходиться в площині\(Q\).
    5. Чотири неколінеарні точки\(I\)\(J\),\(K\),, і\(L\), з відрізками лінії, що з'єднують всі точки один з одним.
    6. Назвіть цей рядок можна п'ятьма способами.
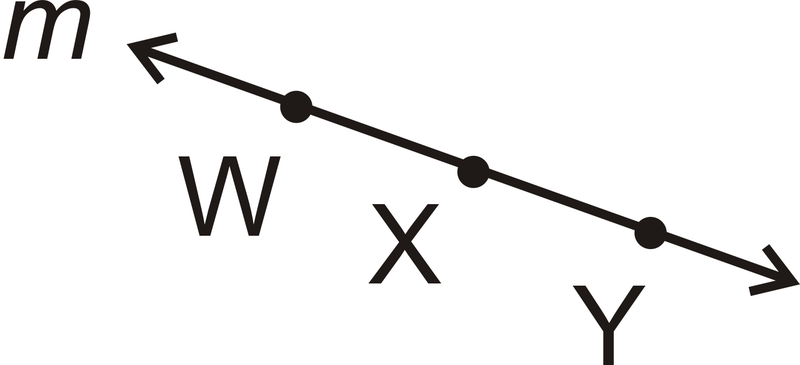
    F-D_453F8A11654C4ФДБ0Ф1ДБ ЕК 475C07F3ЕД АФ 3Б1840 CDC7F61F7D33+зображення_крихіткий+зображення_крихіткий.PNG

    Малюнок\(\PageIndex{18}\)

    1. Назвіть геометричну фігуру можна трьома різними способами.
    F-д_880С43АЕ1А99Е 519998676680 Е4Д20216Б5КСФ 8АА3941994Ф+зображення_крихіткий+зображення_крихіткий_крихіткий.PNG

    Малюнок\(\PageIndex{19}\)

    1. Назвіть геометричну фігуру можна двома різними способами.
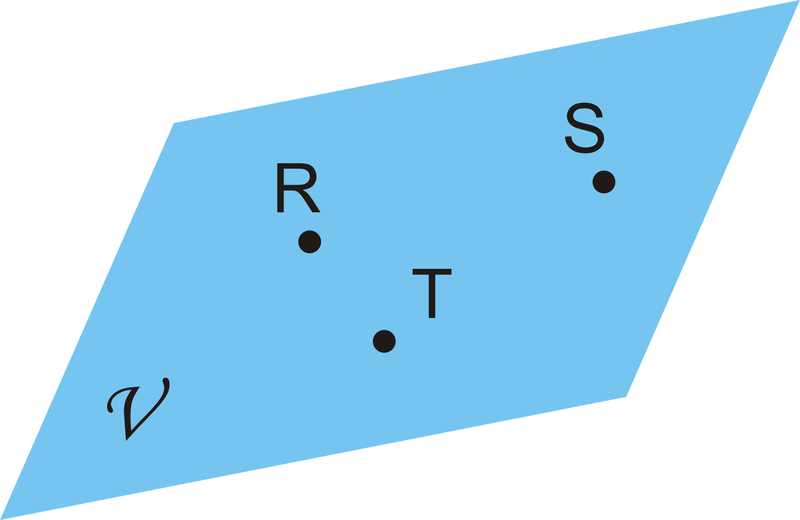
    Ф-д_73д1Ф04Ф5Ф5Ф27395Е43 ЕД ФА35Б96827565Ф53 ЕДФ 55С14235734D2ЦБФ+зображення_крихіткий+зображення_крихіткий.PNG

    Малюнок\(\PageIndex{20}\)

    1. Яка найкраща геометрична модель для футбольного поля? Поясніть свою відповідь.
    2. Перерахуйте два приклади того, де ви бачите промені в реальному житті.
    3. Який тип геометричного об'єкта є перетином прямої і площини? Намалюйте свою відповідь.
    4. У чому різниця між постулатом і теоремою?

    Для 13-16 використовуйте геометричні позначення, щоб максимально детально пояснити кожну картинку.

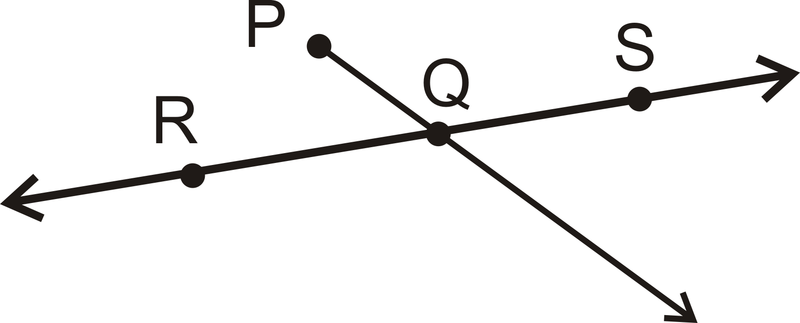
    1. Ф-Д_08332С41Е37Е32А5Б0А50Д9Ф Ф Ед д 23507Б4068Е79ААБ0131615А3+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{21}\)
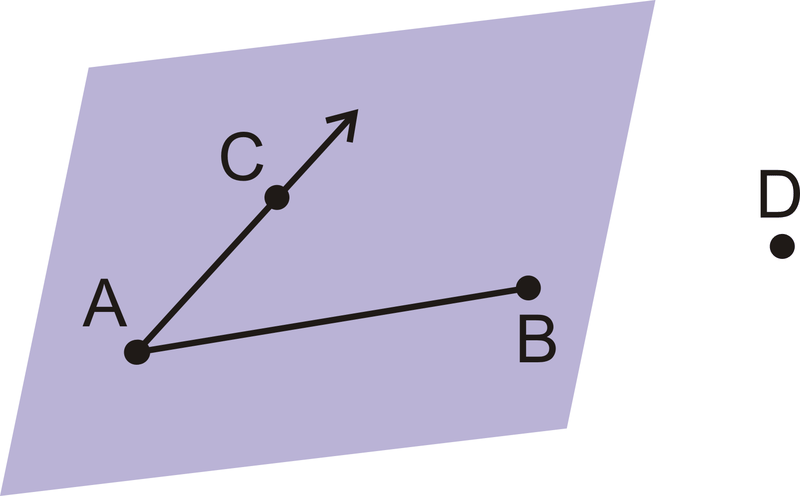
    2. F-D_0A8293A2C800D288218A20 ЕБ 8036375684 С65487 FeAF041EFD75E73+зображення_крихіткий+зображення_крихіткий_png
      Малюнок\(\PageIndex{22}\)
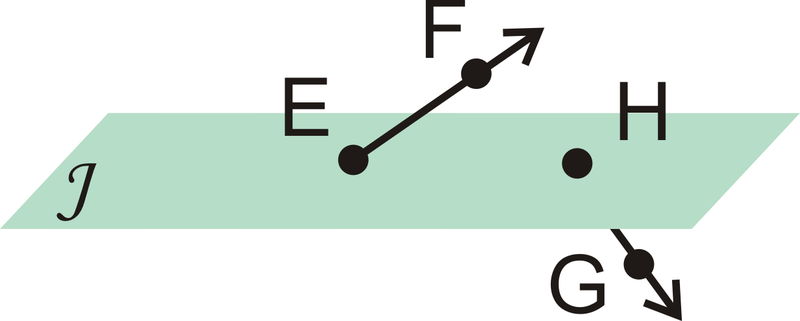
    3. F-д_Д9Е9Б6Д 79Д5А20816Ф6Ф00Б12Ф97184ЕД 34C3A17C2E97ed43 Додано 3+зображення_крихіткий+зображення_крихіткий.PNG

      Малюнок\(\PageIndex{23}\)

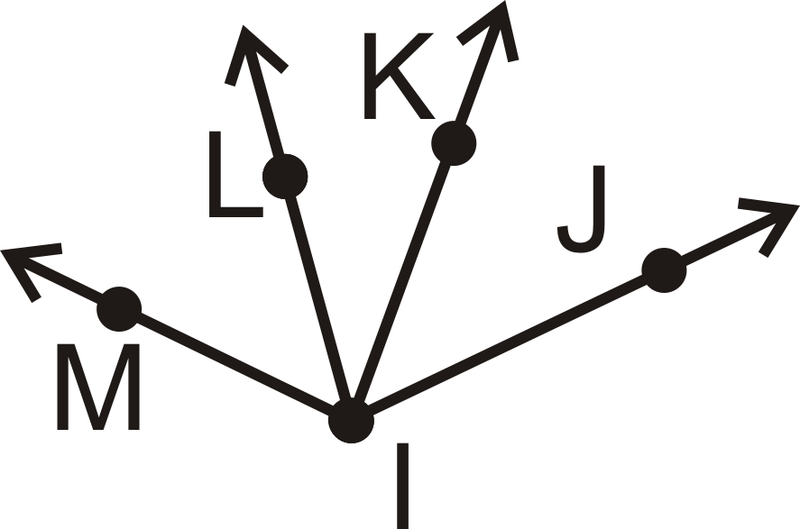
    4. Ф-Д_4БД848Е1924 Е525Ф0Б4ДБ Б 5 ББД Д 34Б27Д8А1А6ДД145Б13А3Б8+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{24}\)

    Для 17-25 визначте, чи є наступні твердження істинними чи хибними.

    1. Будь-які дві точки є колінеарними.
    2. Будь-які три точки визначають площину.
    3. Лінія - це два промені із загальною кінцевою точкою.
    4. Відрізок лінії - це нескінченно багато точок між двома кінцевими точками.
    5. Точка займає місце.
    6. Лінія - одновимірна.
    7. Будь-які чотири точки є копланарними.
    8. \(\overrightarrow{AB}\)можна прочитати «промінь\(AB\)» або «промінь»\(BA\).
    9. \(\overleftrightarrow{AB}\)може бути прочитано «рядок\(AB\)» або «рядок»\(BA\).

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 1.1.

    Лексика

    Термін Визначення
    колінеарний Три і більше точок є колінеарними, коли вони лежать на одній лінії.
    копланарний Точки та/або лінії, розташовані на одній площині, є копланарними.
    кінцева точка Кінцева точка - це точка на одному кінці відрізка лінії або променя.
    перехрестя Точка або набір точок, де лінії, площини, сегменти або промені перетинаються.
    лінія Нескінченно багато точок, які поширюються назавжди в обидві сторони.
    відрізок лінії Відрізок лінії — це частина лінії, яка має дві кінцеві точки.
    літак Площина - це рівна, двовимірна поверхня. Його можна осмислити як аркуш паперу нескінченної площі.
    Точка Точка - це місце в просторі, яке не має розміру або форми.
    постулат Постулат - це твердження, яке приймається як істинне без доказів.
    промінь Частина лінії з однією кінцевою точкою, яка простягається назавжди у напрямку, протилежному цій точці.
    простір Простір - це сукупність всіх точок, що розширюються в трьох вимірах.
    Розміри Розміри - це виміри, які визначають форму і розмір фігури.
    Неколінеарні Неколінеарна точка розташовується над або нижче лінії.
    не-копланарний Некомпланарная точка розташовується над або нижче площини.
    теорема Теорема - це твердження, яке можна довести правдивим за допомогою постулатів, визначень та інших теорем, які вже доведені.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Основні принципи геометричних визначень - Основні

    Діяльність: Основні геометричні визначення Дискусійні питання

    Навчальні посібники: Основи геометрії навчальний посібник

    Практика: Геометрія Терміни

    Реальний світ: основні геометричні визначення