6.1.4: Фокальна властивість еліпсів

Last updated

Oct 27, 2022
Save as PDF
- 6.1.3: Еліпси, які не зосереджені на початку
- 6.2: Параболи

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Фокальна властивість еліпсів

У 1602 році астроном Йоганнес Кеплер працював над проблемою для свого боса Тихо Браге. Він продовжував багатовікове дослідження, намагаючись розробити формулу, яка могла б обчислити орбіти планет, зокрема Марса в цьому випадку. Він працював роками над проблемою з найсучаснішими технологіями того часу, але ніколи не був задоволений результатами, оскільки вони ніколи не були по-справжньому точними або надійними.

Щоб спростити свої розрахунки, він вдарив по концепції, що планета змітає рівні площі простору (в фігурі у формі пирога з сонцем на кінчику) в рівних кількостях часу, незважаючи на відмінності в відстані планети від сонця.

Протягом наступних трьох років він намагався розробити ідеальне рівняння для опису орбіти, яка б відповідала цьому та іншим спостереженням, які він використовував.

Нарешті, в 1605 році він зрозумів, що у нього є відповідь. Його реалізація/відкриття міцно поставило б його як одного з найвідоміших вчених усіх часів.

Що він усвідомив?

Фокальна властивість еліпсів

Еліпси, які не зосереджені на початку

Щоб знайти рівняння для еліпсів, зосереджених навколо іншої точки, скажімо $\ (h, k)$ , просто замініть на $\ x−h$ і $\ x$ $\ y$ з $\ y−k$ . Це змістить усі точки еліпса до правих $\ h$ одиниць (або ліворуч, якщо $\ h<0$ ) та до $\ k$ одиниць вгору (або вниз, якщо $\ k<0$ ). Отже, загальна форма для горизонтально- або вертикально-орієнтованого еліпса така:

$\ \frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1$

Вона зосереджена навколо точки $\ (h,k)$ . Якщо $\ b<a$ , еліпс горизонтально орієнтований і має осередки $\ \left(h+\sqrt{a^{2}-b^{2}}, k\right)$ і $\ \left(h-\sqrt{a^{2}-b^{2}}, k\right)$ на своїй горизонтальній великій осі. Якщо $\ a<b$ , вона вертикально орієнтована і має осередки $\ \left(h, k+\sqrt{a^{2}-b^{2}}\right)$ і $\ \left(h, k-\sqrt{a^{2}-b^{2}}\right)$ на своїй вертикальній великій осі.

Приклади

Приклад 1

Раніше вам задавали питання про проблему, над якою працював астроном Йоганнес Кеплер для свого боса Тихо Браге.

Рішення

Усвідомлення Кеплера полягало в тому, що, хоча він навмисно уникав їх протягом дуже довгого часу, тому що вони були такими простими, еліпси були ідеальною формою, щоб всі його розрахунки зійшлися разом.

Коли планета обертається навколо Сонця (або коли будь-який об'єкт обертається навколо будь-якого іншого), вона проходить еліптичний шлях, і сонце лежить в одному з двох осередків еліпса. Закони Кеплера щодо руху планет досить точні, щоб виробляти сучасні обчислення, які досі використовуються для прогнозування руху штучних супутників сьогодні.

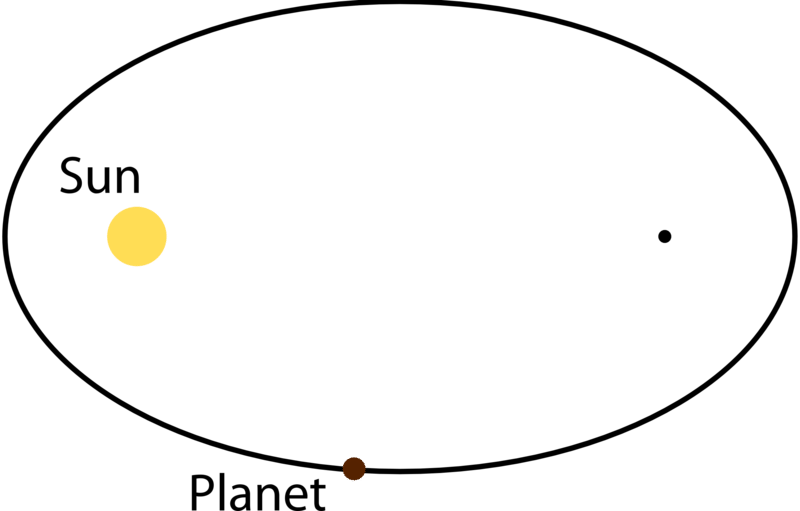
F-D_3473F1F1F16ЕФД5 CFB80C1012Ф2Д5Д568Д4де 52Ф71Е2229Е90ЕА5+зображення_крихіткий+зображення_крихіткий.PNG

Приклад 2

Поясніть, чому віднімання $\ h$ від $\ x$ −члену та $\ k$ з $\ y$ −члена у рівнянні для еліпса зміщує еліпс $\ h$ горизонтально та $\ k$ вертикально.

Рішення

Якщо $\ (x,y)$ це рішення $\ \frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1$

$\ (x+h, y+k)$ то це рішення $\ \frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1$

Це створює графік, який зсувається горизонтально на $\ h$ і вертикально $\ k$ .

Приклад 3

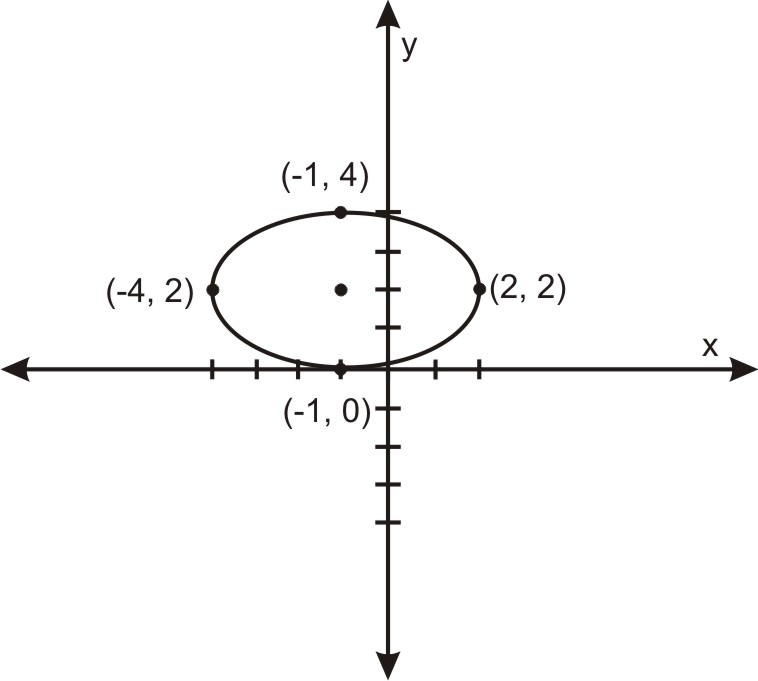
Графік рівняння $\ 4 x^{2}+8 x+9 y^{2}-36 y+4=0$ .

Рішення

Нам потрібно отримати рівняння у вигляді загального рівняння вище. Перший крок - згрупувати всі $\ x$ члени та $\ y$ члени, перерахувати наші провідні коефіцієнти $\ x^{2}$ і $\ y^{2}$ , і перемістити константи на іншу сторону рівняння:

$\ 4\left(x^{2}+2 x\right)+9\left(y^{2}-4 y\right)=-4$

Тепер ми «завершуємо квадрат», додавши відповідні терміни до $\ x$ виразів та $\ y$ виразів, щоб зробити ідеальний квадрат.

$\ 4\left(x^{2}+2 x+1\right)+9\left(y^{2}-4 y+4\right)=-4+4+36$

Тепер множимо і ділимо на коефіцієнти, щоб отримати:

$\ \frac{(x+1)^{2}}{9}+\frac{(y-2)^{2}}{4}=1$

І ось у нас воно є. Як тільки він знаходиться в цій формі, ми бачимо, що це еліпс по центру навколо точки (-1,2), він має горизонтальну велику вісь довжини 3 і вертикальну незначну вісь довжини 2, і з цього ми можемо зробити ескіз еліпса:

Ф-Д_Б2887БА 53БДСД 6ФА46Б875381Д8 CFB65C8EEEEE5Ф550050Ф16С32C5E+зображення_крихіткий+зображення_крихіткий.jpg

Приклад 4

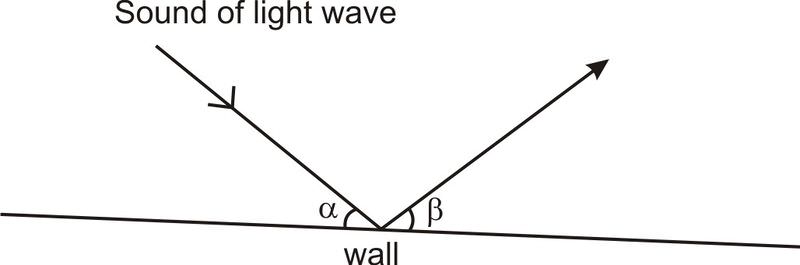
Національний скульптурний зал у Капітальному будинку Сполучених Штатів є прикладом кімнати у формі еліпса, яку іноді називають «кімнатою відлуння», яка забезпечує цікаве застосування властивості еліпсів. Якщо людина дуже тихо шепоче на один з вогнищ, звук перегукується таким чином, що людина в іншому вогнищі часто може почути їх дуже чітко. Подейкують, що Джон Квінсі Адамс скористався цією властивістю, щоб підслуховувати розмови в цій кімнаті.

Як Echo номери працюють? Яке відношення має до цього еліптична форма кімнати?

Рішення

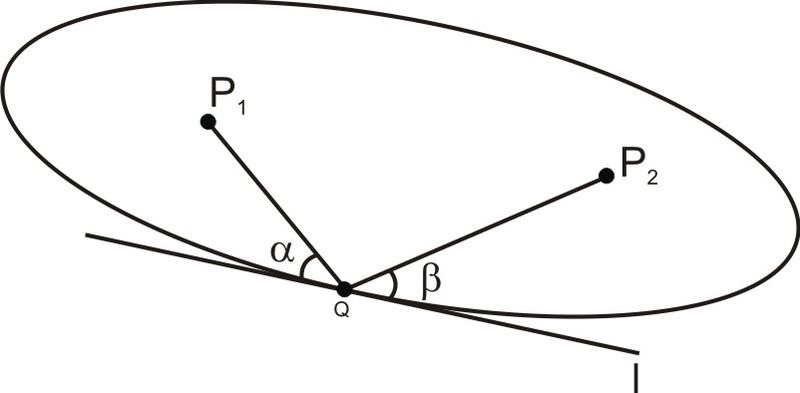
Властивість еліпсів, що змушує ехо-кімнати працювати, називається «оптичним властивістю». Так навіщо відлуння, якщо це оптична властивість? Ну і світлові промені і звукові хвилі відскакують навколо подібними способами. Зокрема, вони обидва відскакують від стін під рівними кутами. На схемі нижче, $\ α=β$ .

Ф-Д_Е86Б55де 91КС39257 БЕ 765ФББ Б Б Б 3ФБ Б 67 Додати 5C9A324464999017+зображення_крихіткий+зображення_крихіткий.jpg

Для криволінійної стіни вони відскакують під рівними кутами до дотичної лінії в цій точці:

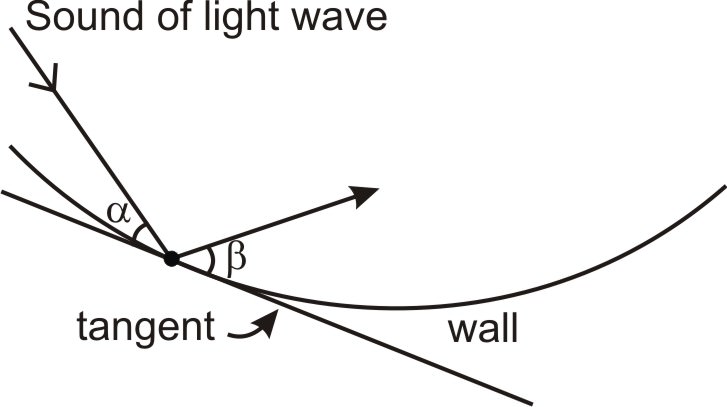
Ф-Д_135Б700Д2С68811355 ЕФ402С1Е64Е3Е3Е1Ф57К9Б793А1Е76053E+зображення_крихіткий+зображення_крихіткий.jpg

Отже, «оптична властивість» еліпсів полягає в тому, що лінії між точкою на еліпсі і двома осередками утворюють рівні кути дотичної в цій точці, або, іншими словами, шепіт, що надходить від одного вогнища, відскакує безпосередньо до інших вогнищ. На схемі нижче, для кожного $\ Q$ на еліпсі, $\ \angle \alpha \cong \angle \beta$ .

Ф-Д_22Ф9ФБ 6398 ААЕ1Ф62720БА9 CFD БДБ Б 8С84БЦК Е33КД7 СЭБ2397E237+зображення_крихіткий+зображення_крихіткий.jpg

Приклад 5

Хоча планети проходять еліптичний шлях навколо Сонця, ці еліпси часто мають дуже низький ексцентриситет, тобто вони близькі до кіл. Діаграма вище перебільшує еліптичну форму орбіти планети. Орбіта Землі має ексцентриситет 0,0167. Його мінімальна відстань від сонця - 146 млн км. Яка його максимальна відстань від сонця? Якщо діаметр Сонця становить 1,4 мільйона кілометрів, чи обидва осередки орбіти Землі лежать всередині Сонця?

Рішення

Нагадаємо, що ексцентриситет еліпса дорівнює $\ \varepsilon=\frac{\sqrt{a^{2}-b^{2}}}{a}$

Припустимо, що орбіта Сонця - це еліпс з центром (0,0). Тоді ми можемо використовувати відстань від початку до фокусу, $\ \sqrt{a^{2}-b^{2}}$ щоб встановити рівняння $\ 146+146+2 \sqrt{a^{2}-b^{2}}=2 a$ і $\ 0.167=\frac{\sqrt{a^{2}-b^{2}}}{a}$ . Розв'язуючи отримуємо $\ a=175.270, b=175.245$ і відстань від (0, 0) до вогнищ, $\ c$ =2.927 (всі одиниці знаходяться в мільйоні км). Нарешті максимальна відстань від землі до сонця становить приблизно 152 мільйони км. З закону Кеплера ми знаємо, що один з вогнищ його орбіти знаходиться в центрі сонця. Інші вогнища - 2 (2.927) =5.854 мільйонів кілометрів, тому він знаходиться поза сонцем (але не дуже далеко!)

Приклад 6

Яка сума відстаней до вогнищ точок на вертикально орієнтованому еліпсі?

Рішення

Приклад 7

Спробуйте скласти графік еліпса: $\ 3 x^{2}-12 x+5 y^{2}+10 y-3=0$ . Що йде не так?

Рішення

Після завершення квадрата ми маємо суму позитивних чисел, що дорівнює від'ємному числу. Це неможливість, тому рівняння не має розв'язків.

Приклад 8

Графік еліпса (точки графіка): $\ 5 x^{2}-15 x-2 y^{2}+8 y-50=0$ . Чим тут відрізняється? Поясніть, як ви думаєте, графік цього рівняння може виглядати.

Рішення

Після завершення квадрата $\ x$ термін і $\ y$ термін є протилежними знаками. Якщо ви намалюєте деякі точки, ви побачите, що графік має два нероз'єднаних ділянки. Про цей клас конічних перерізів піде мова в уроці по гіперболам.

Рецензія

Графік наведені нижче більш просунуті еліпси.

$\ (x)^{2}+\frac{(y+2)^{2}}{9}=1$
$\ \frac{(x+2)^{2}}{4}+(y+2)^{2}=1$
$\ \frac{(x+2)^{2}}{9}+(y)^{2}=1$
$\ \frac{(x-1)^{2}}{9}+\frac{(y-4)^{2}}{16}=1$
$\ 4(x-1)^{2}+9(y)^{2}=36$
$\ (x+1)^{2}+\frac{(y-1)^{2}}{9}=1$
$\ (x-4)^{2}+\frac{(y+3)^{2}}{16}=1$
$\ \frac{(x)^{2}}{16}+\frac{(y)^{2}}{9}=1$
$\ 4(x+1)^{2}+(y-3)^{2}=16$
$\ (x+4)^{2}+\frac{(y-1)^{2}}{16}=1$

Графік наступні еліпси особливого випадку.

$\ (x+4)^{2}+(y+2)^{2}=4$
$\ (x+2)^{2}+(y)^{2}=16$
$\ (x-3)^{2}+(y-2)^{2}=1$
$\ (x+2)^{2}+(y-1)^{2}=9$
$\ (x-3)^{2}+(y-1)^{2}=9$
Що спільного у цих еліпсів?

Дайте відповідь на наступні проблеми слів.

Хоча еліптичні шляхи планет - це еліпси, які тісно наближені колами, комети та астероїди часто мають орбіти, які є еліпсами з дуже високим ексцентриситетом. Комета Галлея має ексцентриситет 0,967 і знаходиться в межах 54,6 мільйона миль від Сонця в найближчій точці, або «перигелії». Яку найдальшу точку вона досягає від сонця?
Обчисліть площу еліпса за допомогою рівняння $\ \frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1$ (Підказка: використовуйте геометричний аргумент, що починається з площі кола.)
Спроектуйте максимально можливу кімнату відлуння з наступними обмеженнями: Ви хотіли б шпигувати за тим, хто буде знаходитися в 3 м від кінчика еліпса. Приміщення не може бути шириною більше 100 м в будь-яку сторону. Як далеко від людини, за якою ви шпигуєте, ви будете стояти?
Незалежно від того, яка орієнтація палиці, якщо ви простежите шлях, який тінь кінчика робить на рівній поверхні, ви виявите, що це еліпс. Опишіть, чому це правда.

Огляд (Відповіді)

Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 6.2.

Ресурси

Лексика

Термін	Визначення
Завершення площі	Завершення квадрата - поширений метод переписування квадратики. Це стосується створення ідеального квадратного триноміала шляхом додавання квадрата 1/2 коефіцієнта члена x.
Конічна	Конічні перерізи - це ті криві, які можуть бути створені перетином подвійного конуса і площини. Вони включають кола, еліпси, параболи та гіперболи.
Ексцентриситет	Ексцентриситет конічного перерізу - це міра того, наскільки конічний переріз відхиляється від кругового. Ексцентриситет кіл дорівнює 0, ексцентриситет еліпсів - між 0 і 1, ексцентриситет парабол - 1, а ексцентриситет гіпербол більше 1. Для еліпсів і гіпербол, $\ e=\frac{c}{a}$ .
Еліпс	Еліпси - це конічні зрізи, які мають вигляд витягнутих кіл. Еліпс представляє всі місця в двох вимірах, які знаходяться на однаковій відстані від двох заданих точок, які називаються вогнищами.
еліпси	Еліпси - це конічні зрізи, які мають вигляд витягнутих кіл. Еліпс представляє всі місця в двох вимірах, які знаходяться на однаковій відстані від двох заданих точок, які називаються вогнищами.
вогнища	Вогнища еліпса - це дві точки, які визначають еліпс. Сума відстаней від будь-якої точки на еліпсі до вогнищ постійна.
Велика вісь	Велика вісь еліпса - це найдовший діаметр еліпса.
незначна вісь	Мала вісь еліпса - це найкоротший діаметр еліпса.
стандартна форма	Стандартна форма еліпса з центром $\ (h,k)$ - це $\ \frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1$ .