6.1.2: Рівняння еліпса

Рівняння еліпса

Кен має незгоду зі своїм другом Скоттом. Скотт каже, що доріжка, на якій вони бігають у школі, насправді не еліпс, а овал. Кен вважає, що це дурна відмінність, оскільки овали та еліпси - це одне і те ж. Хто правий?

---

Рівняння еліпса

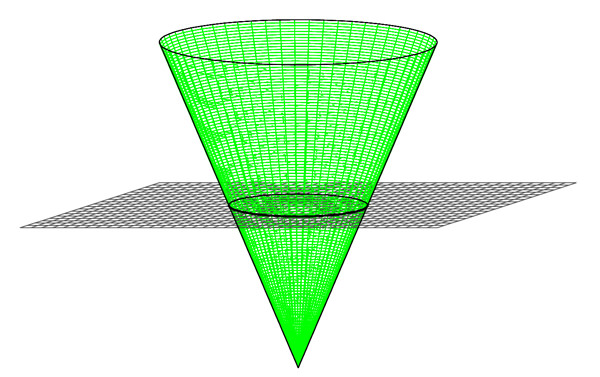
Коли площина «прорізає» одну сторону конуса, ми отримуємо або коло, або об'єкт «овальної форми», як показано нижче. Виявляється, це не звичайний овал, а щось називається еліпсом, фігурою з особливими властивостями.

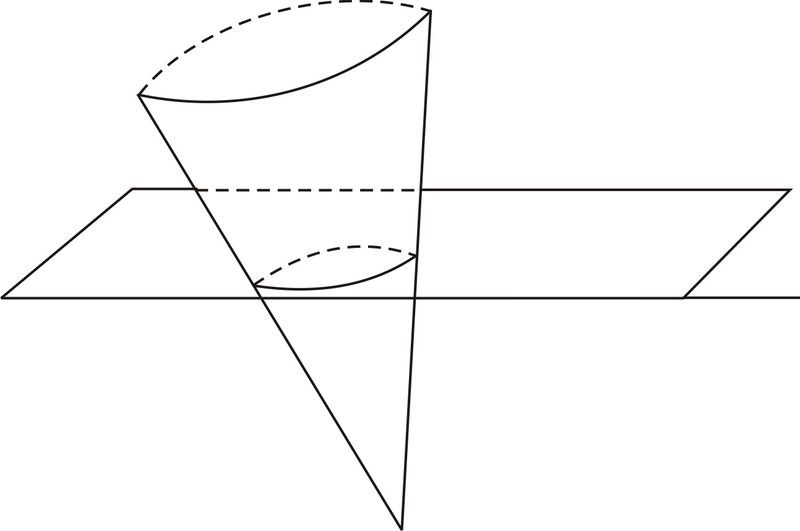
а. конус «прорізаний» площиною 90 ^о до осі конуса, щоб утворити коло.		б. конус «прорізаний» площиною під кутом, щоб сформувати еліпс.

Еліпси можуть бути визначені деякими їх властивостями. Один із способів визначення еліпса - це «витягнуте коло». Це форма, яку ви отримаєте, якщо ви намалювали коло на спущеній повітряній кулі, а потім розтягнули повітряну кулю рівномірно у двох протилежних напрямках:

Це також форма поверхні води, яка виникає, коли ви нахиляєте круглу склянку:

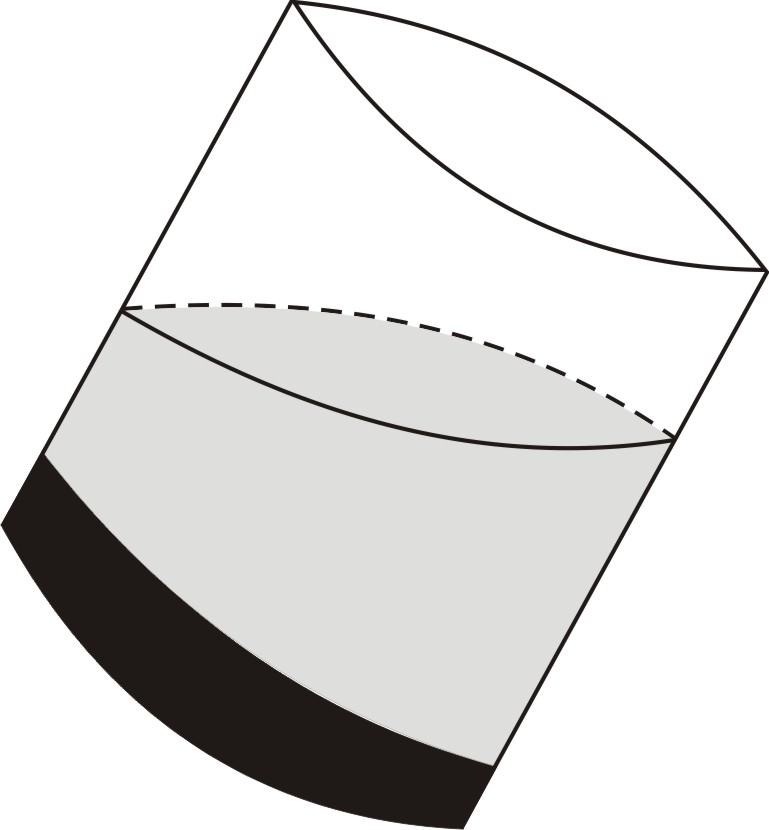
Або еліпс можна розглядати як форму кола, намальованого на аркуші паперу, коли його розглядають під кутом.

Рівняння еліпсів

Цю «розтяжку» можна уявити алгебраїчно. Для простоти візьміть коло радіусом 1 по центру у початку (0,0). Формула відстані говорить нам, що це множина точок (x, y), яка є відстанню на 1 одиницю від початку.

\ (\\ почати {вирівнювання}
D &=\ sqrt {\ ліворуч (x_ {1} -x_ {2}\ праворуч) ^ {2} +\ ліворуч (y_ {1} -y_ {2}\ праворуч) ^ {2}}\\ 1 &=\ sqrt {(x-0) ^ {2} + (y-0) ^ {2}}\\
1 &=\ sqrt {(x-0) ^ {2} + (y-0) ^ {2}}\\
1 &= {x-0) ^ {2} 2} +y^ {2}
\ кінець {вирівняний}\)

Це рівняння може бути змінено таким чином\(\ x^{2}+y^{2}=1\), щоб розтягнути коло у горизонтальному (тобто осі x) напрямку шляхом ділення\(\ x\) змінної на константу\(\ a>1\),

\(\ \left(\frac{x}{a}\right)^{2}+y^{2}=1\)

Чому це розтягує коло по горизонталі? Ну, ефект ділення\(\ x\) на\(\ a\) полягає в тому, що для кожного\(\ y\) −значення в впорядкованій парі,\(\ (x, y)\) яка задовольняє вихідному рівнянню, відповідне\(\ x\) значення потрібно помножити на\(\ a\), щоб пара зробила рішення зміненого рівняння. Так\(\ (x, y)\) розв'язки кола знаходяться в однозначній відповідності з розв'язками\(\ (ax, y)\) зміненого рівняння, отже, розтягування відповідного графіка вліво і вправо на множник\(\ a\).

Ось графік\(\ \left(\frac{x}{2}\right)^{2}+y^{2}=1\):

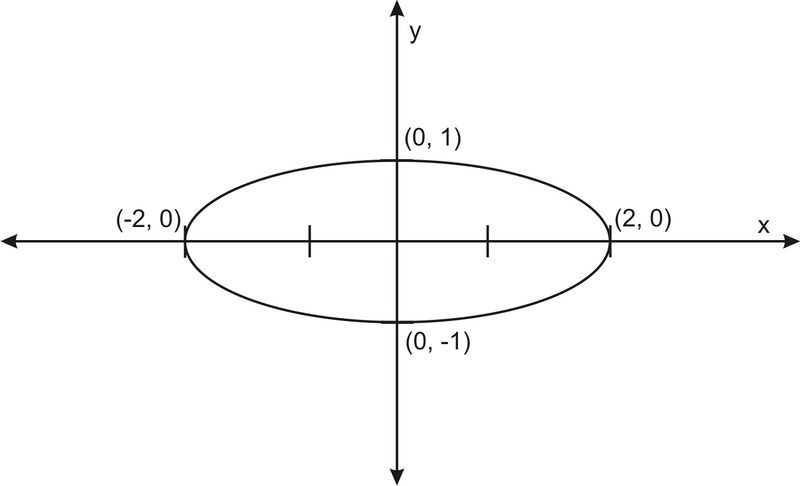
Узагальнюючи рівняння шляхом дозволу розтягування у вертикальному напрямку, отримаємо наступне.

\(\ \left(\frac{x}{a}\right)^{2}+\left(\frac{y}{b}\right)^{2}=1\)

Фактор\(\ a\) розтягує коло в горизонтальному напрямку, а фактор\(\ b\) розтягує коло у вертикальному напрямку. Якщо\(\ a=b\), це всього лише коло. Коли\(\ a \neq b\), це рівняння являє собою еліпс. Еліпс розтягується в горизонтальному напрямку, якщо\(\ b<a\) і він розтягується у вертикальному напрямку, якщо\(\ a<b\).

Часто вищевказане рівняння записується наступним чином.

\(\ \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)

Це називається стандартною формою рівняння еліпса, припускаючи, що еліпс знаходиться в центрі (0, 0).

Щоб намалювати графік еліпса за допомогою рівняння\(\ \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\), почніть з побудови чотирьох осей перехоплення, які легко знайти, підключивши 0 для x, а потім для y, Потім намалюйте еліпс від руки, або за допомогою графічної програми або калькулятора.

вогнища

У кожному еліпсі є дві спеціальні точки, які називаються вогнищами (вогнища множини, фокус - однини), які лежать всередині еліпса і які можуть бути використані для визначення форми. Для еліпса з центром (0,0), який ширше, ніж він високий, його головна вісь горизонтальна, а осередки - на\(\ \left(\sqrt{a^{2}-b^{2}}, 0\right)\) і\(\ \left(-\sqrt{a^{2}-b^{2}}, 0\right)\).

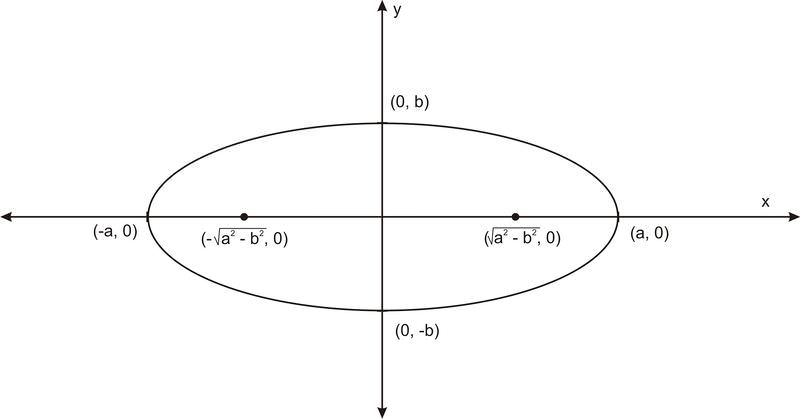
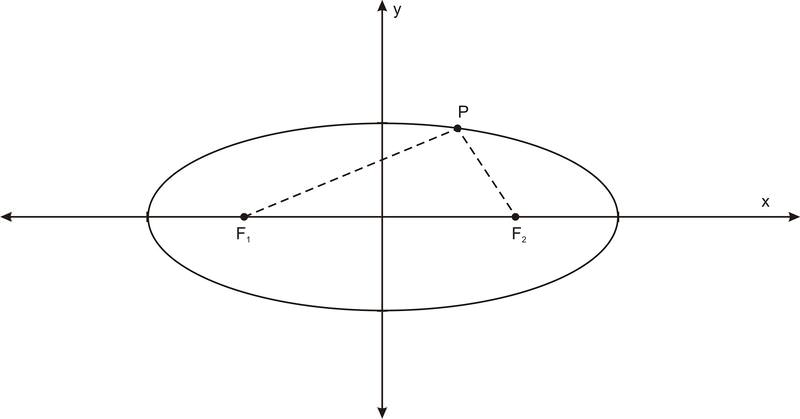
Яке значення цих пунктів? Еліпси стосуються цих точок так само, як коло відноситься до його центру. Пам'ятайте, що коло може розглядатися як множина точок у площині, які є певною відстанню від центральної точки, насправді, це, як правило, визначення кола. Ну а вогнища діють як центр хіба що їх два. Еліпс - це множина точок, де сума відстані між кожною точкою на еліпсі і кожним з двох вогнищ є постійним числом. На схемі нижче, для будь-якої точки\(\ P\) на еліпсі\(\ F_{1} P+F_{2} P=d\), де\(\ F_{1}\) і\(\ F_{2}\) знаходяться вогнища і\(\ d\) є константою.

---

Приклади

Приклад 1

Раніше вам давали питання про незгоду Кена і Скотта.

Рішення

Скотт має рацію. Овали - це не те саме, що еліпси.

Приклад 2

Намалюйте графік\(\ \frac{x^{2}}{4}+\frac{y^{2}}{9}=1\).

Рішення

Це рівняння можна переписати як\(\ \frac{x^{2}}{2^{2}}+\frac{y^{2}}{3^{2}}=1\).

Для ескізу ми встановлюємо\(\ x=0\) і вирішуємо,\(\ y\) щоб знайти\(\ x\) -перехоплення\(\ y=0\) і встановити і\(\ x\) вирішити для пошуку\(\ y\) − перехоплення.

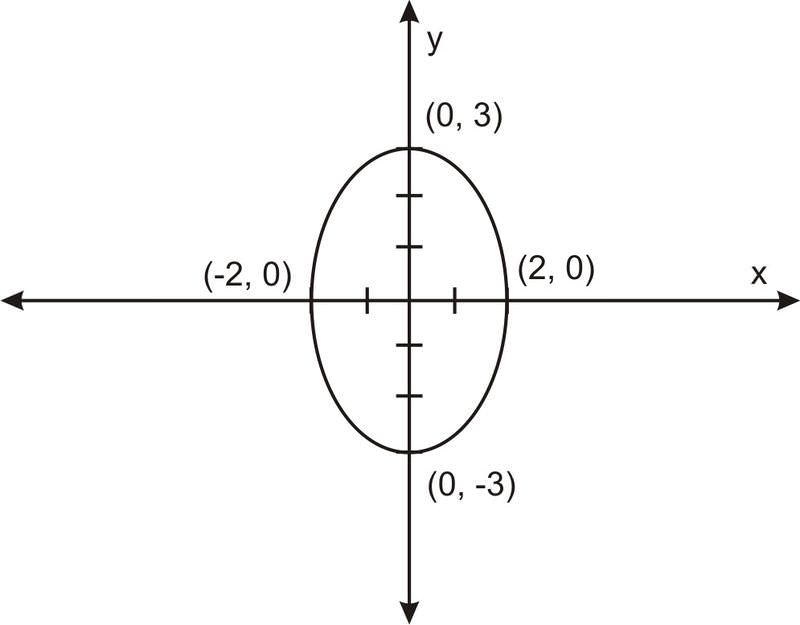
Чотири точки, які ми отримуємо, є (0, 3), (0, -3), (2, 0) та (-2, 0).

Намалюйте ці точки та намалюйте еліпс:

Приклад 3

Намалюйте графік\(\ \frac{x^{2}}{16}+y^{2}=1\).

Рішення

Це можна переписати як\(\ \frac{x^{2}}{4^{2}}+\frac{y^{2}}{1^{2}}=1\). Після знаходження перехоплень і замальовування графіка тим же процесом, що і вище, ми маємо:

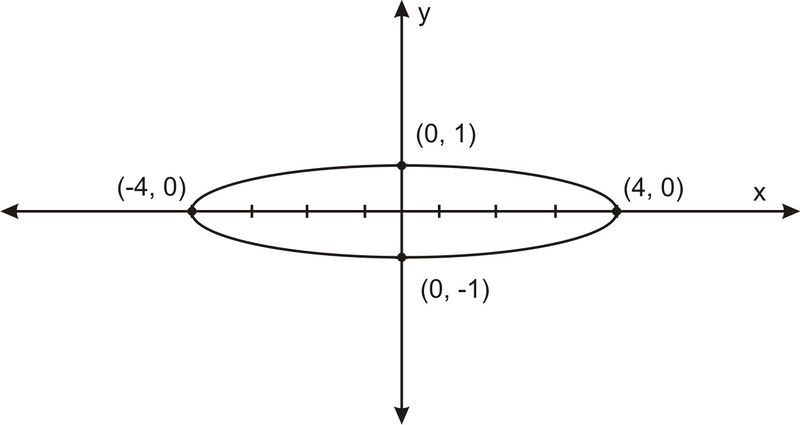
Відрізок, що охоплює довгий напрямок еліпса, називається великою віссю, а сегмент, що охоплює короткий напрямок еліпса, називається незначною віссю. Таким чином, в останньому прикладі велика вісь - це відрізок від (-4, 0) до (4, 0), а незначна вісь - відрізок від (0, -1) до (0, 1).

Основні та другорядні осі є прикладами того, що іноді називають опорними лініями. Аполлоній, давньогрецький математик, який написав ранній трактат про коніки, використовував ці та інші опорні лінії для орієнтації конічних перерізів. Хоча греки не використовували координатну площину для обговорення геометрії, ці опорні лінії пропонують перспективу обрамлення, подібну до декартової площини, яку ми використовуємо сьогодні. Спосіб Аполлонія обрамлення коніків опорними лініями був найближчою математикою, яка прийшла до системи координатної геометрії, яку ви так добре знаєте до систематичної роботи Декарта та Ферма в сімнадцятому столітті.

Приклад 4

Який повний діапазон ексцентриситету еліпса? Як він виглядає поблизу крайнощів цього діапазону?

Рішення

Вогнища можна використовувати для вимірювання того, наскільки еліпс «витягнутий» від кола. Символ\(\ \varepsilon\) позначає ексцентриситет еліпса, і він визначається відстанню між вогнищами, розділеними на довжину великої осі, або\(\ \frac{\sqrt{a^{2}-b^{2}}}{a}\) для горизонтально орієнтованих еліпсів і\(\ \frac{\sqrt{b^{2}-a^{2}}}{b}\) для вертикально орієнтованих еліпсів. Оскільки коло є еліпсом\(\ a=b\), де кола мають ексцентриситет 0.

Інтервал можливих значень дорівнює\(\ \varepsilon \in[0,1)\). В\(\ \varepsilon=0\), еліпс являє собою коло; з наближенням ексцентриситету 1 він стає все більш і більш витягнутим.

Приклад 5

Не всі рівняння для еліпсів починаються у стандартній формі вище. Наприклад,\(\ 25 x^{2}+9 y^{2}=225\) це еліпс. Помістіть його в належному вигляді і побудуйте графік.

Рішення

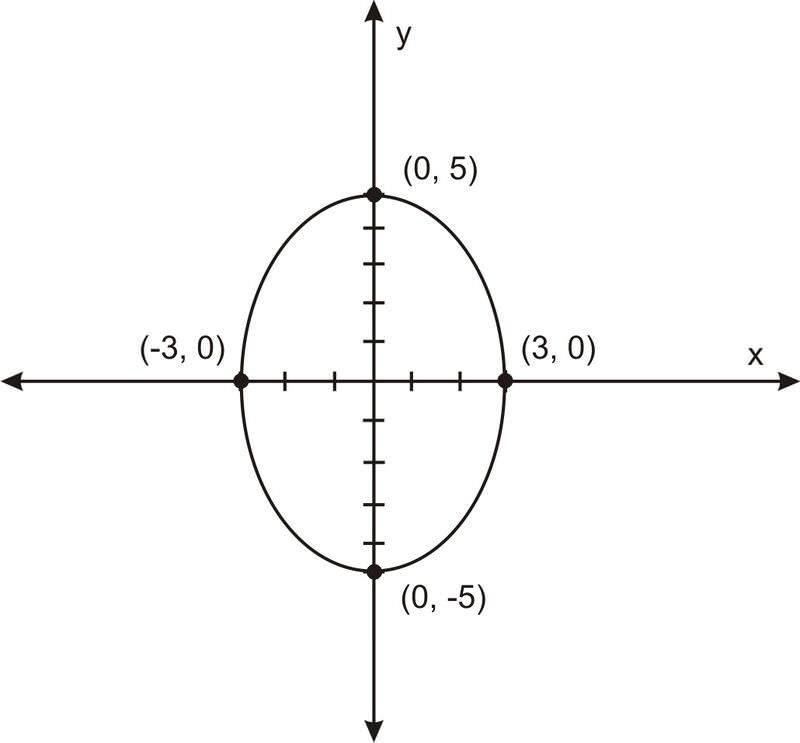
Щоб графувати\(\ 25 x^{2}+9 y^{2}=225\) як еліпс:

\(\ \frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)... Спочатку розділіть обидві сторони на 225

\(\ \frac{x^{2}}{3^{2}}+\frac{y^{2}}{5^{2}}=1\)... Знайдіть перехоплення

Графік, у нас є:

Приклад 6

Вище згадувалося, що при нахилі круглого склянки води поверхня води являє собою еліпс. Використовуючи наше робоче визначення еліпса як «витягнутого кола», поясніть, чому, на вашу думку, вода приймає таку форму.

Рішення

Відповіді можуть відрізнятися, але слід пояснити, чому форма, яка виходить, розтягує коло в одному напрямку, оскільки ширина скла постійна.

Приклад 7

Спробуйте намалювати цей еліпс, де цифри не виявляються такими акуратними:\(\ 3 x^{2}+4 y^{2}=12\).

Рішення

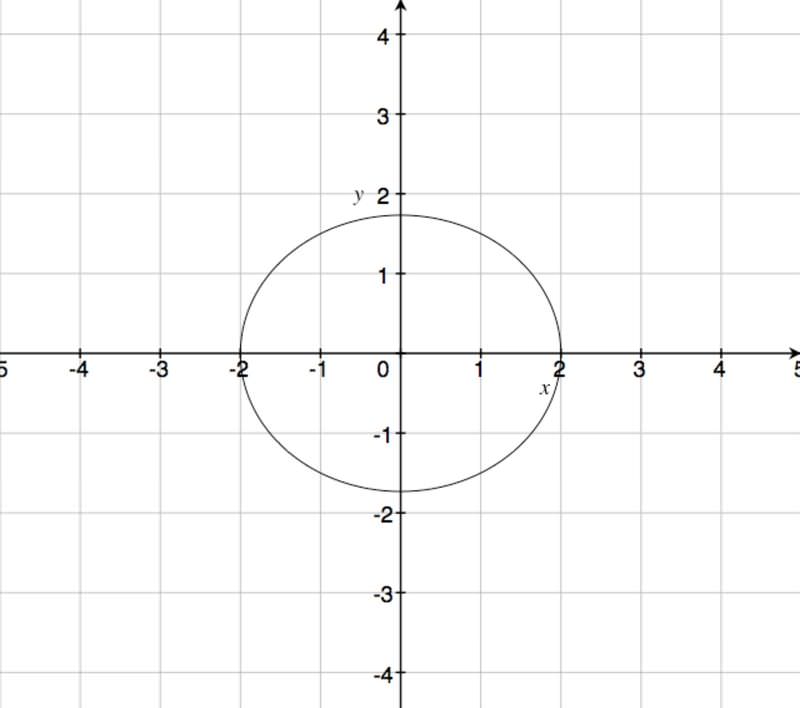
Для графіка\(\ 3 x^{2}+4 y^{2}=12\):

\(\ \frac{x^{2}}{4}+\frac{y^{2}}{3}=1\)... Спочатку розділіть обидві сторони на 12

\(\ \frac{x^{2}}{2^{2}}+\frac{y^{2}}{\sqrt{3}^{2}}=1\)... Знайдіть перехоплення

Графікуючи, отримуємо:

---

Рецензія

Перетворіть кожне рівняння в стандартну форму еліпса.

1. \(\ x^{2}+4 y^{2}=4\)
2. \(\ 9 x^{2}+16 y^{2}=144\)
3. \(\ 25 x^{2}+36 y^{2}=900\)
4. \(\ 36 x^{2}+9 y^{2}=324\)
5. \(\ 49 x^{2}+y^{2}=49\)
6. \(\ 16 x^{2}+4 y^{2}=64\)
7. \(\ x^{2}+2 y^{2}=2\)
8. \(\ 3 x^{2}+4 y^{2}=12\)
9. \(\ 5 x^{2}+6 y^{2}=30\)
10. \(\ 6 x^{2}+3 y^{2}=18\)
11. \(\ 7 x^{2}+y^{2}=7\)
12. \(\ 4 x^{2}+2 y^{2}=8\)

Графік наведені нижче еліпси.

13. \(\ 9 x^{2}+16 y^{2}=144\)
14. \(\ 49 x^{2}+y^{2}=49\)
15. \(\ x^{2}+2 y^{2}=2\)
16. \(\ 7 x^{2}+y^{2}=7\)

---

Огляд (Відповіді)

Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 6.1.

---

Лексика

Термін	Визначення
Конус	Конус являє собою суцільну об'ємну фігуру з круглим підставою і однією вершиною.
Конічна	Конічні перерізи - це ті криві, які можуть бути створені перетином подвійного конуса і площини. Вони включають кола, еліпси, параболи та гіперболи.
Ексцентриситет	Ексцентриситет конічного перерізу - це міра того, наскільки конічний переріз відхиляється від кругового. Ексцентриситет кіл дорівнює 0, ексцентриситет еліпсів - між 0 і 1, ексцентриситет парабол - 1, а ексцентриситет гіпербол більше 1. Для еліпсів і гіпербол,\(\ e=\frac{c}{a}\).
Еліпс	Еліпси - це конічні зрізи, які мають вигляд витягнутих кіл. Еліпс представляє всі місця в двох вимірах, які знаходяться на однаковій відстані від двох заданих точок, які називаються вогнищами.
еліпси	Еліпси - це конічні зрізи, які мають вигляд витягнутих кіл. Еліпс представляє всі місця в двох вимірах, які знаходяться на однаковій відстані від двох заданих точок, які називаються вогнищами.
вогнища	Вогнища еліпса - це дві точки, які визначають еліпс. Сума відстаней від будь-якої точки на еліпсі до вогнищ постійна.
Велика вісь	Велика вісь еліпса - це найдовший діаметр еліпса.
незначна вісь	Мала вісь еліпса - це найкоротший діаметр еліпса.
стандартна форма	Стандартна форма еліпса з центром\(\ (h, k)\) - це\(\ \frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\).