4.4.3: Системи полярних рівнянь

Ви, ймовірно, пам'ятаєте, що коли ви графуєте кілька рівнянь на одній лінії, ви зазвичай отримуєте місця на графіку, де вони перетинаються (якщо ви не графуєте паралельні лінії!).

Те ж саме відбувається і при побудові рівнянь у полярній формі та/або на полярному графіку. Коли ви графуєте перетин декількох полярних рівнянь, ви розглядаєте їх так само, як і прямокутні рівняння, графуєте обидва і знаходите області, які є істинними для обох рівнянь.

Системи полярних рівнянь

Полярні рівняння можуть бути побудовані за допомогою полярних координат. Відображення двох полярних рівнянь на одному наборі осей може призвести до того, що точка (и) перетину.

Усі точки на полярному графіку є координатами, які роблять рівняння дійсним. Координати точки (ів) перетину при заміні в кожне рівняння зроблять обидва рівняння дійсними.

Одним із методів пошуку точки перетину для двох полярних графіків є встановлення рівнянь, рівних один одному.

Назвіть перше рівняння r ₁ і друге рівняння r ₂.

Точки перетину знаходяться при r ₁ = r ₂, тому встановіть рівняння рівні, а потім вирішуйте отримане тригонометричне рівняння.

Приклади

Приклад 1

Знайти перетин\(\ r_{1}=3 \sin \theta\) і\(\ r_{2}=\sqrt{3} \cos \theta\)

Рішення

Встановіть рівняння, рівні один одному:\(\ 3 \sin \theta=\sqrt{3} \cos \theta\)

розділіть обидві сторони рівняння на cos θ і 3:\(\ \frac{3 \sin \theta}{3 \cos \theta}=\frac{\sqrt{3} \cos \theta}{3 \cos \theta}\)

Спростити:\(\ \frac{\sin \theta}{\cos \theta}=\frac{\sqrt{3}}{3}\)

Використовуйте посвідчення:\(\ \frac{\sin \theta}{\cos \theta}=\tan \theta\)

\(\ \tan \theta=\frac{\sqrt{3}}{3}\)

\(\ \theta=\frac{\pi}{6} \text { or } \frac{7 \pi}{6}\)

підставити\(\ \frac{\pi}{6}\) в будь-якому рівнянні для отримання\(\ r=1.5\)

підставити\(\ \frac{7 \pi}{6}\) в будь-якому рівнянні, щоб отримати -1,5

ПРИМІТКА: координати\(\ \left(1.5, \frac{\pi}{6}\right)\) і\(\ \left(-1.5, \frac{7 \pi}{6}\right)\) представляють однакову полярну точку, тому існує лише одне рішення цього рівняння.

Ми закінчили? Якщо подивитися на графіки r ₁ і r ₂, то можна побачити, що є ще одна точка перетину:

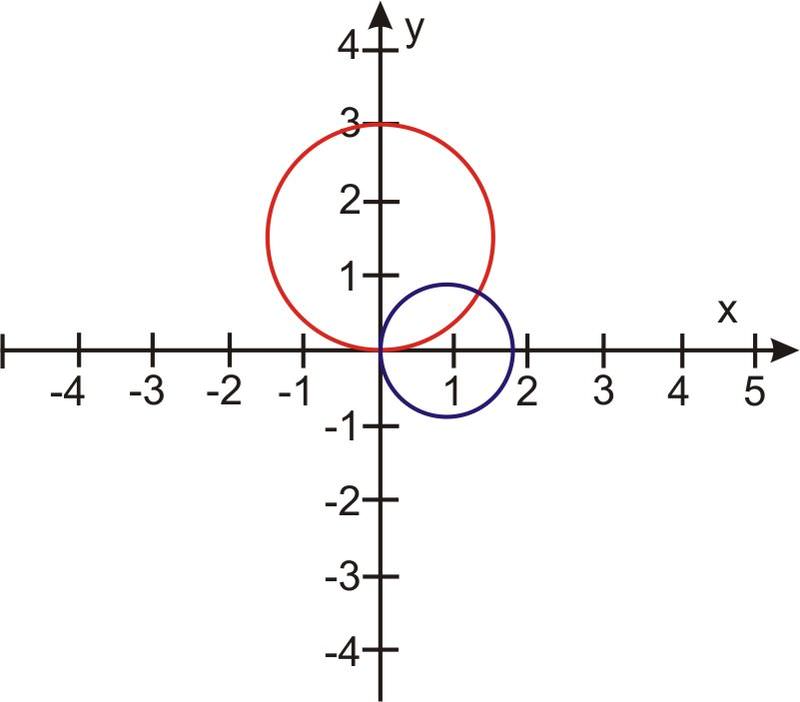
Ф-Д_7Б5Б5БД83С9Д2А50Б9Б9Ф4С0854ЕББ1С5Ф8АФ601ФЕ7Ф7Ф711Б3С35Д+зображення_крихіткий+зображення_крихіткий.jpg

коли θ = 0, r ₁ = 3 грін θ = 3 грін (0) = 0

Це означає, що r ₁ = 3 sin θ проходить через полюс (0, 0).

Для r ₂: коли\(\ \theta=\frac{\pi}{2}\), r ₂ = 0 тобто r ₂ =\(\ \sqrt{3} \cos \theta\) проходить через точку\(\ \left(0, \frac{\pi}{2}\right)\).

Тому обидва графіки проходять через полюс і полюс є точкою перетину.

Полюс НЕ був виявлений як точка перетину за допомогою першого кроку! (Чому? Підказка: Скільки існує способів представлення полюса в полярних координатах?) Це показує нам, що після того, як ви використовуєте алгебраїчні методи для пошуку перетинів у точках, відмінних від полюса, ви також повинні перевірити наявність перетинів на полюсі.

Приклад 2

Знайдіть точку (и) перетину для двох графіків:\(\ r_{1}=1 \text { and } r_{2}=2 \sin 2 \theta\).

Рішення

Встановіть r ₁ = r ₂ і вирішіть:

\ (\\ begin {масив} {l}
1=2\ sin 2\ тета\\
\ frac {1} {2} =\ sin 2\ тета
\ кінець {масив}\)

Використовуйте заміну\(\ \alpha=2 \theta\) для вирішення

\ (\\ begin {масив} {l}
\ frac {1} {2} =\ sin\ альфа\
\ альфа =\ гідророзриву {\ pi} {6},\ frac {5\ pi} {6}
\ end {масив}\)

Так як\(\ \alpha=2 \theta\), рішення для\(\ \theta\) дає нам

\(\ \theta=\frac{\pi}{12}, \frac{5 \pi}{12}\)

Але, нагадаємо, що θ має діапазон 0 ≤ θ ≤ 2 π. Оскільки ми розв'язали з 0 ≤ α ≤ 2 π, нам насправді потрібно враховувати значення θ з 0 ≤ θ ≤ 4 π. Чому? Нагадаємо, що sin (2 θ) має два цикли між 0 і 2 π, і тому ми додаємо ще два рішення,

\(\ \alpha=\frac{13 \pi}{6}, \frac{17 \pi}{6}\)

і з тих пір\(\ \alpha=2 \theta\),

\(\ \theta=\frac{13 \pi}{12}, \frac{17 \pi}{12}\)

Нарешті, нам потрібно розглянути розв'язки, коли r = -1, оскільки r = 1 і r = -1 - це одне і те ж полярне рівняння. Отже, рішення

\(\ -\frac{1}{2}=\sin \alpha\)

\(\ \alpha=\frac{7 \pi}{6}, \frac{11 \pi}{6}\)

Знову ж таки, використання α = 2 θ і додавання розв'язків для повторення дає нам ще чотири рішення,

\(\ \theta=\frac{7 \pi}{12}, \frac{11 \pi}{12}, \frac{19 \pi}{12}, \frac{21 \pi}{12}\)

Таким чином, в цілому, є вісім рішень цього набору рівнянь.

ПРИМІТКА: Нагадаємо, що рішення тригонометричних рівнянь, де кут дорівнює θ, вимагає розгляду всіх потенційних значень між 0 і 2π. Коли кут дорівнює 2θ, як і в цьому випадку, обов'язково шукайте всі потенційні значення між 0 і 4π. Коли кут дорівнює 3θ, як і в цьому випадку, обов'язково шукайте всі потенційні значення між 0 і 6π., і так далі.

Оскільки r ₁ не може дорівнювати 0, полюс не знаходиться на його графіку і не є точкою перетину.

Графік показує вісім точок перетину, які були знайдені раніше.

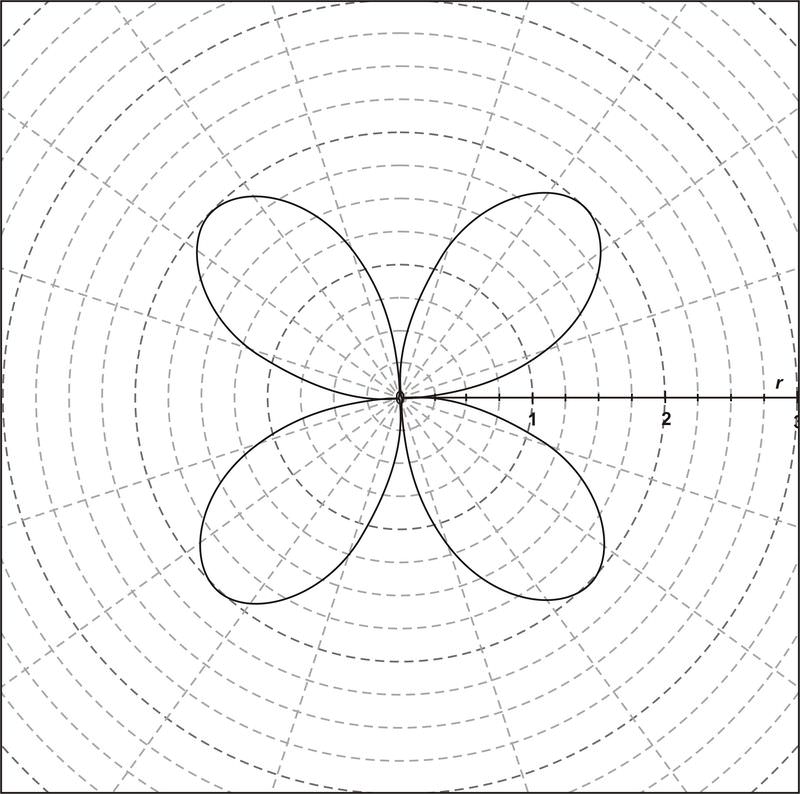
Ф-Д_Б321289 Деф 2Б07Ф906КД20АД092ФБ5А44Д1ДЕ 20Е6952Б4ФБ0Ф328ФА+зображення_крихіткий+зображення_крихіткий.jpg

Приклад 3

Знайти точку (и) перетину, якщо така існує, для наступної пари рівнянь: r ₁ = 2 і r ₂ = secθ.

Рішення

Тут ми будемо використовувати таблицю значень для кожної функції, вирішуючи за квадрантом. Нагадаємо, що період сек θ дорівнює 2π.

Для першого квадранта:

θ (кут)	0	π/6	π/4	π/3	π/2
r ₁ (відстань)	2	2	2	2	2
р ₂	1	1.15	1.4	2	унд

Для другого квадранта:

θ (кут)	2π/3	3π/4	5π/6	π
r ₁ (відстань)	2	2	2	2
р ₂	-2	-1.4	-1.15	-1

Для третього квадранта:

θ (кут)	7π/6	5π/4	4π/3	3π/2
r ₁ (відстань)	2	2	2	2
р ₂	-1.15	-1.4	-2	унд

Для четвертого квадранта:

θ (кут)	5π/3	7π/4	11π/6	2π
r ₁ (відстань)	2	2	2	2
р ₂	2	1.4	1.15	1

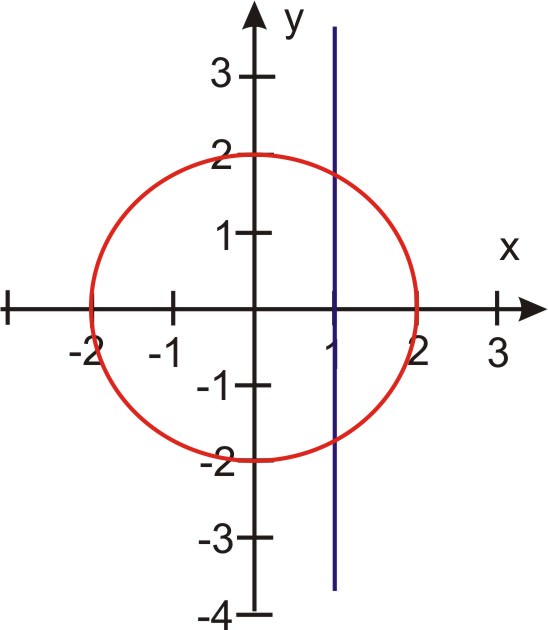
Ф-Д_44553349Д9Е3Ф11Ф86СЕ 90169Ф3ДФД637Б0С008ФД5Е18098АФ957643+зображення_крихіткий+зображення_крихіткий.jpg

Зверніть увагу, що ^3-й і ^4-й квадранти повторюють значення ^1-го і ^2-го квадрантів.

Зауважте в таблиці значень, що (2, π/3) і (2, 5π/3) є точками перетину. Подивіться на криві - перше рівняння дає коло, а друге дає лінію. Максимальна кількість точок, що перетинаються для прямої та кола, дорівнює 2. Два пункти були знайдені.

Приклад 4

Знайдіть точку (и) перетину для цієї пари полярних рівнянь: r = 2+ 4 sinθ та θ = 60°.

Рішення

Рівняння θ = 60 ^o - це лінія, що робить кут 60° з віссю r.

Складіть таблицю значень для r = 2 + 4 sin θ

Для першого квадранта:

θ (кут)	0	30	45	60	90
R (відстань)	2	4	4.83	5.46	6

Для другого квадранта:

θ (кут)	120	135	150	180
R (відстань)	5.46	4.83	4	2

Для третього квадранта:

θ (кут)	210	225	240	270
R (відстань)	0	-.83	-1.46	-2

Для четвертого квадранта:

θ (кут)	300	315	330	360
R (відстань)	-1.46	-.83	0	2

Зверніть увагу, що в табл., (60, 5.46) і (240, -1.46) = (60, 1.46). Нагадаємо, що при r < 0 ви будуєте точку (r, θ), обертаючи 180 ^o (або π).

Нарешті, нам потрібно перевірити полюс: r = 2 + 4 sin θ проходить через полюс для θ = 330 ^о, а θ = 60 ^o також проходить через полюс. Таким чином, третя точка перетину дорівнює (0, 0).

Ф-Д_9439515Ф18Б15Б15Б17352371С5Ф1А9ДФ Ф 656 ФЕБК 132683870А5ФА+зображення_крихіткий+зображення_крихіткий.jpg

Приклад 5

Знайдіть точку (и) перетину для цієї пари полярних рівнянь: r ₁ = 2 cosθ і r ₂ = 1.

Рішення

Складіть стіл:

Для першого квадранта:

θ (кут)	0	π/6	π/4	π/3	π/2
r ₁ (відстань)	2	\(\ \sqrt{3}\)	\(\ \sqrt{2}\)	1	0
р ₂	1	1	1	1	1

Для другого квадранта:

θ (кут)	2π/3	3π/4	5π/6	π
r ₁ (відстань)	-1	\(\ -\sqrt{2}\)	\(\ -\sqrt{3}\)	-2
р ₂	1	1	1	1

Для третього квадранта:

θ (кут)	7π/6	5π/4	4π/3	3π/2
r ₁ (відстань)	\(\ -\sqrt{3}\)	\(\ -\sqrt{2}\)	-1	0
р ₂	1	1	1	1

Для четвертого квадранта:

θ (кут)	5π/3	7π/4	11π/6	2π
r ₁ (відстань)	1	\(\ \sqrt{2}\)	\(\ \sqrt{3}\)	2
р ₂	1	1	1	1

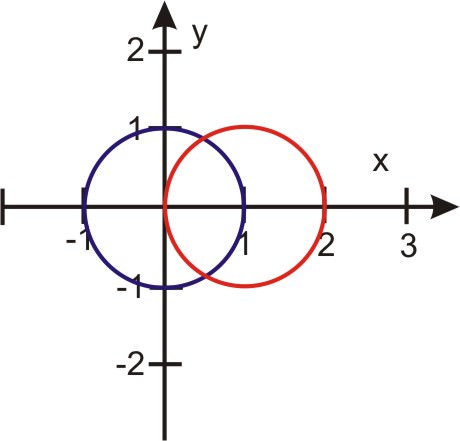
Таким чином, унікальні рішення знаходяться на\(\ \theta=\frac{\pi}{3}, \frac{4 \pi}{3}\). У цьому наборі також є два повторюваних рішення (чи можете ви їх знайти?).

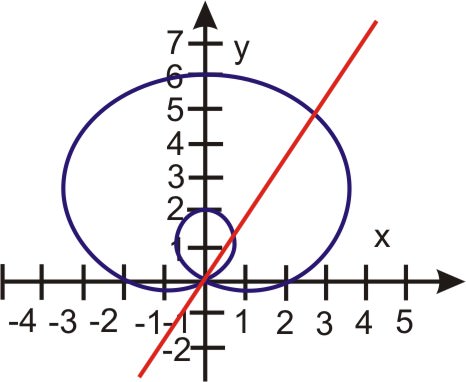
Ось графік, що показує два рішення:

F-д_ДК 3Е20А2659ФД 3БД ДДД 759089 ФА66Е367БДБ2Е247Д1СА0Д7БДД 3Д7БДД 6+зображення_крихіткий+зображення_крихіткий.jpg

Рецензія

Графіки r=1 і r=2cosθ наведені нижче.

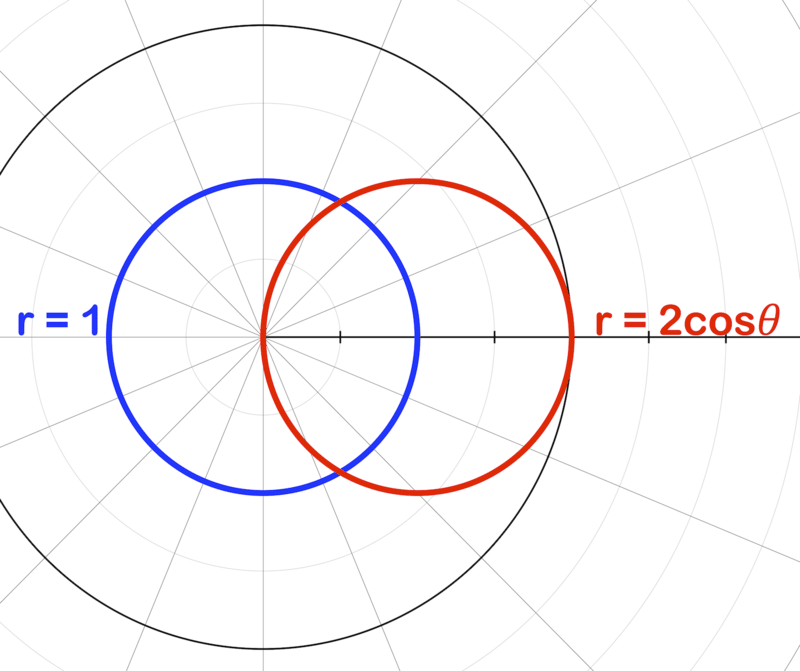
F-D_ЕД 25 де 03539С422Д440БД64С3389780 ББФ 73ЕФКД 9347612407D56D29+зображення_крихіткий+зображення_крихіткий.PNG

Скільки разів вони перетинаються?
У яких квадрантах вони перетинаються?
У яких точках відбуваються перехрестя?

На основі наведеного нижче зображення та наступної інформації: перетин графіків r=cosθ та r=1−cosθ

Визначте, скільки разів вони перетинаються?
У яких точках відбуваються перехрестя?

Знайдіть точки перетину наступних пар кривих.

r=2 р=2кост
r = sin2θ r = 2sinθ
r=2+2sinθ r = 2−2cosθ
r=3cosθ r = 2−кост

Знайти точку (и) перетину для кожної системи рівнянь. Графік для перевірки вашого рішення.

\(\ r_{1}=\csc \theta\ r_{2}=2 \sin \theta\)
\(\ r_{1}=\cos \theta\ r_{2}=1+\sin \theta\)
\(\ r_{1}=\sin \theta\ r_{2}=\sin 2 \theta\)
\(\ r_{1}=-4 \sin \theta\ r_{2}=-4 \cos \theta\)
\(\ r_{1}=1-2 \sin \theta\ r_{2}=\sqrt{9 \cos (\theta)}\)
\(\ r_{1}=1-\cos \theta\ r_{2}=4 \cos (3 \theta)\)

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 4.3.

Лексика

Термін	Визначення
Конічна	Конічні перерізи - це ті криві, які можуть бути створені перетином подвійного конуса і площини. Вони включають кола, еліпси, параболи та гіперболи.
Точки перетину	Точки перетину - це місця, де два різних рівняння мають однакові рішення.
полярні координати	Полярні координати описують розташування на сітці за допомогою полярної системи координат. Розташування кожної точки визначається її відстанню від полюса і його кутом по відношенню до полярної осі.
полюс	Полюс - це центральна точка на полярному графіку.
квадрант	Квадрант - це одна четверта координатної площини. Чотири квадранти нумеруються за допомогою римських цифр I, II, III та IV, починаючи у верхньому правому куті та збільшуючись проти годинникової стрілки.