Skip to main content
LibreTexts - Ukrayinska

4.4.1: Полярні координати

  1. Last updated
  2. Save as PDF
  • Page ID
    55014

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Полярні координати

    Всі мріяли літати в той чи інший час. Мало того, що було б набагато менше трафіку, щоб турбуватися про, але напрямки були б набагато простішими!

    Ходьба або водіння: «Ідіть на схід 2 квартали, поверніть ліворуч, потім на північ 6 блоків. Дочекайтеся поїзда. Поверніть направо, схід ще 3 блоки, обережно корови! Поверніть ліворуч, йдіть на північ ще 4 квартали і паркуйтеся».

    Політ: «Літайте 30 град на схід від півночі трохи менше 11 і 1/4 блоків. Земля».

    Приємний сон, але яке відношення це має до полярних координат?

    Полярні координати

    Полярна система координат є альтернативою декартовій системі координат, яку ви використовували в минулому для графічних функцій. Полярна система координат спеціалізується на візуалізації та маніпуляції кутами.

    Кути ідентифікуються шляхом переміщення проти годинникової стрілки навколо кругового графіка від лінії 0 град або осі r (де буде вісь + x) до заданого кута.

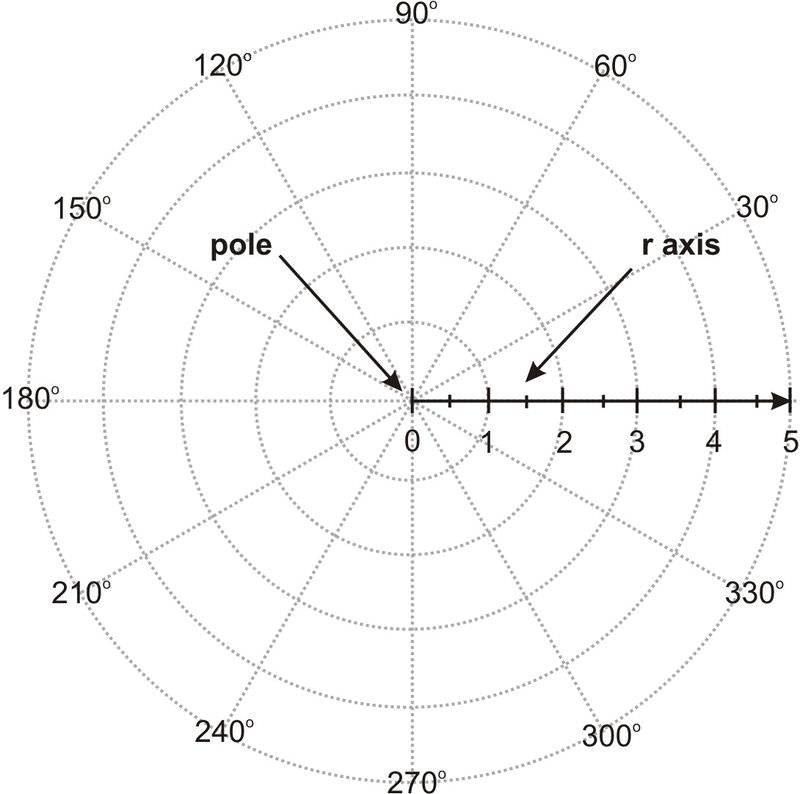    Ф-Д_ПК-ДФ 27Д83Е18011ДАД 541 А377СА59488БК 86ССК410551А71ЕБ79А9+зображення_крихіткий+зображення_крихіткий.jpg[Малюнок 1]

    Для побудови певної точки спочатку пройдіть вздовж осі r на r одиниць. Потім поверніть проти годинникової стрілки на заданий кут, зазвичай представлений «θ». Будьте обережні, щоб використовувати правильні одиниці виміру кута (радіани або градуси).

    Радіани

    Зазвичай полярні графіки робляться з радіанами (особливо якщо вони включають тригонометричні функції), але іноді використовуються градуси.

    Радіан - це кут, утворений між віссю r та полярною віссю, намальованою для задоволення ділянки окружності, яка є тією ж довжиною, що і радіус кола.

    Враховуючи, що окружність кола дорівнює 2π⋅r, а оскільки r - радіус, це означає, що в повному колі є 2π радіани, а 1π радіани в 1/2 кола.

    Якщо 1/2 кола дорівнює π радіани, і 180 град, це означає, що в кожному радіані є\(\ \frac{180}{\pi}\) градуси.

    Це означає приблизно 57,3 градусів = 1 радіан.

    Графік за допомогою технології

    Полярні рівняння можна графікувати за допомогою графічного калькулятора: За допомогою графічного калькулятора - перейдіть до MODE. Там виберіть RADIAN для вимірювання кута і POL (для Polar) на лінії FUNC (функція). При натисканні Y = зверніть увагу, що рівняння змінилося з y = на r =. Туди введіть полярне рівняння. Після натискання графіка, якщо ви не бачите повний графік, відрегулюйте x - і y - max/min тощо у ВІКНО.

    "рамка = «0" висота = «450px» ім'я = «92048" src =» https://www.ck12.org/flx/show/video/...nates-Overview "URL-адресу мініатюри ="» заголовок = «Відеооб'єкт? хеш = 1a6cbeee9e3598a31394e80c1e6462fd» дата завантаження = «2016-07-06 23:19:25" ширина =» 95% «>

    Приклади

    Приклад 1

    Покладіть точки на графіку полярних координат: точка A\(\ \left(2, \frac{\pi}{3}\right)\), точка B (4, 135 o) та точка C\(\ \left(-2, \frac{\pi}{6}\right)\)

    Рішення

    Нижче знаходиться полюс, полярна вісь і точки A, B і C.

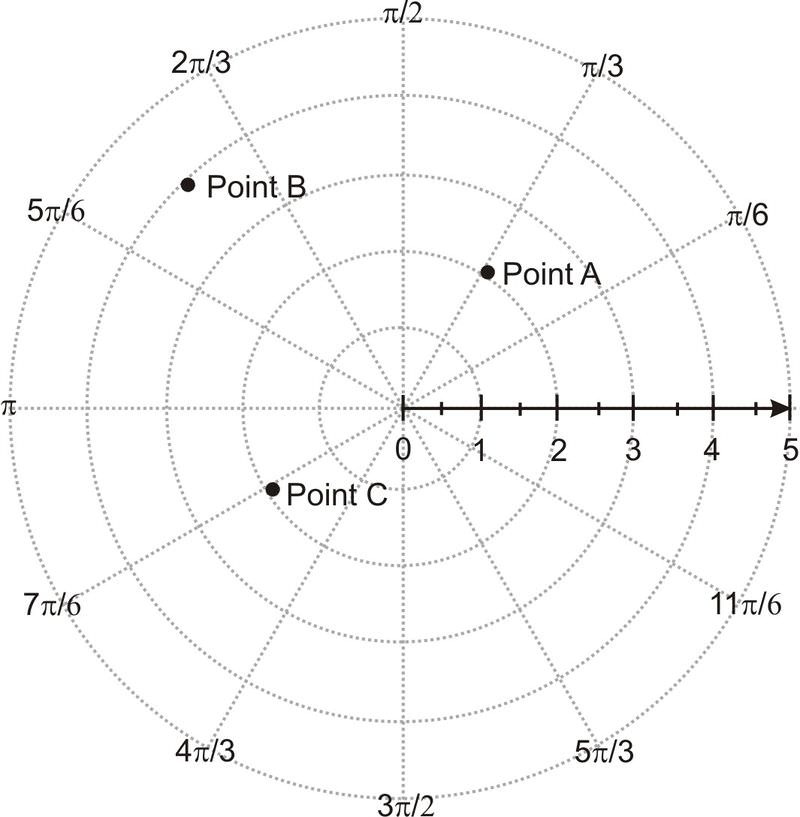    Ф-Д_45279С3164Д72 АА30БК 907КС78577Ф3А446Б590А7А7603563ДЕ5Б25БК+зображення_крихіткий+зображення_крихіткий.jpg[Малюнок 2]
    Приклад 2

    Побудуйте наступні пункти.

    1. (4, 30 о)
    2. (2.5,\(\ \pi\))
    3. \(\ \left(-1, \frac{\pi}{3}\right)\)
    4. \(\ \left(3, \frac{5 \pi}{6}\right)\)
    5. (−2, 300 о)

    Рішення

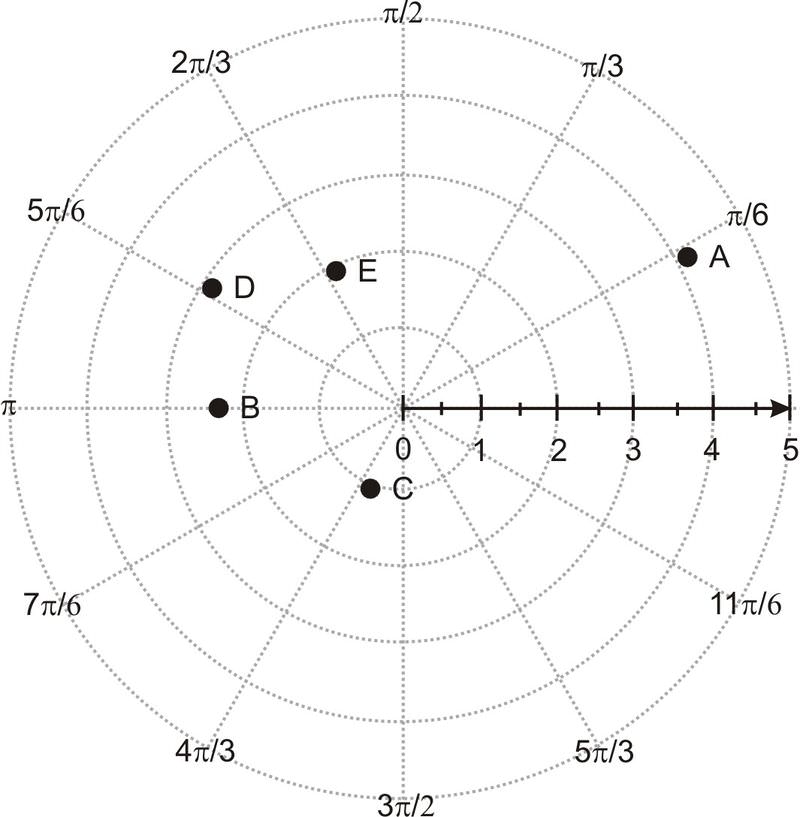    Ф-Д_9А4А4А 1287КФ13 ФАФА-4Ф8118ФЦ75СА57Е906АФ30ДФ296Ф3ЕЕ0С7504С+зображення_крихіткий+зображення_крихіткий.jpg[Малюнок 3]
    Приклад 3

    Використовуйте графічний калькулятор або програму побудови графіків для побудови наступних рівнянь.

    1. r = 1+3sinθ
    2. r = 1+2коСθ

    Рішення

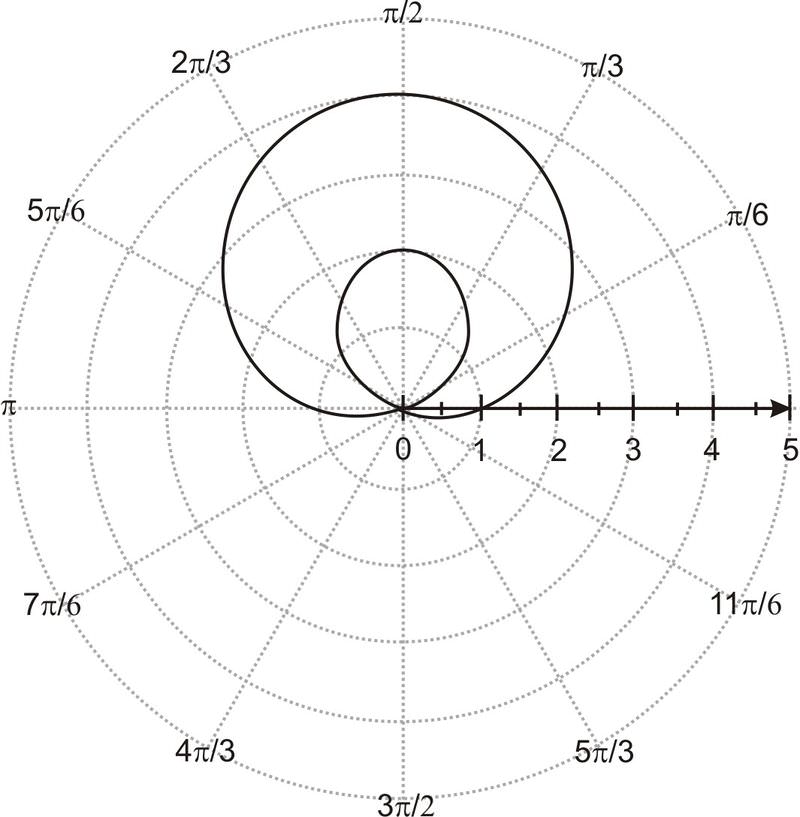
    1. Ф-Д_86957457Д9Ф7Ф7С34991 БА 3БДФ 2А548А7954527Е8Б5Ф5Ф729Б738235+зображення_крихіткий+зображення_крихіткий.jpg
    2. Перегляньте наведені вище кроки під графіком за допомогою технології, якщо у вас виникли проблеми.
    Приклад 4

    Перетворення з радіанів в градуси.

    Нагадаємо, що\(\ \pi r a d=180^{\circ} \text { and } 1 \mathrm{rad}=\frac{180}{\pi} \approx 57.3^{\circ}\)

    1. \(\ \frac{\pi}{2}\)
    2. 5.17
    3. \(\ \frac{3 \pi}{2}\)

    Рішення

    1. Якщо\(\ \pi r a d=180^{\circ}\) тоді\(\ \frac{\pi}{2} r a d=90^{\circ}\)
    2. Якщо\(\ 1 rad \approx 57.3^{\circ}\) тоді\(\ 5.17 rad \approx 296^{\circ}\)
    3. Якщо\(\ \pi r a d=180^{\circ}\) тоді\(\ \frac{3 \pi}{2} r a d=270^{\circ}\)
    Приклад 5

    Перетворення з градусів в радіани.

    Нагадаємо, що\(\ \frac{180^{\circ}}{\pi}=57.3^{\circ} \approx 1 \mathrm{rad}\).

    1. 251 г
    2. 360 о
    3. 327 г

    Рішення

    1. Якщо\(\ 57.3^{\circ} \approx 1rad\) тоді\(\ 251^{\circ} \approx 4.38 \mathrm{rad} \approx 1.4 \pi \mathrm{rad}\)
    2. Якщо\(\ 57.3^{\circ} \approx 1 rad\) тоді\(\ 360^{\circ} \approx 6.28 rad\)
    3. Якщо\(\ 57.3^{\circ} \approx 1 rad\) тоді\(\ \frac{327^{\circ}}{57.3^{\circ}} \approx 5.71 rad\)
    Приклад 6

    Перетворити з градусів в радіани, відповісти з точки зору π.

    Нагадаємо, що 2πrad = 360o і, отже, πrad=180 o.

    1. 90 г
    2. 270 о
    3. 45 о

    Рішення

    1. Якщо\(\ \pi r a d=180^{\circ}\) тоді\(\ \frac{\pi}{2} r a d=90^{\circ}\)
    2. Якщо\(\ \pi r a d=180^{\circ} \text { and } \frac{\pi}{2} r a d=90^{\circ}\) тоді\(\ 1 \frac{1}{2} \pi r a d \rightarrow \frac{3}{2} \pi \rightarrow \frac{3 \pi}{2} r a d=270^{\circ}\)
    3. Якщо\(\ \frac{\pi}{2} r a d=90^{\circ}\) тоді\(\ \frac{\pi}{4} r a d=45^{\circ}\)

    Рецензія

    1. Чому точка на площині не може бути позначена за допомогою унікальної впорядкованої пари (r, θ).
    2. Поясніть, як графік (r, θ), якщо r360<0 and/or θ>.

    Графік кожної точки на полярній площині.

    1. \(\ \text{A}\left(6,145^{\circ}\right)\)
    2. \(\ \text{B} (-2, \frac{13\pi}{6})\)
    3. \(\ \text{C} (\frac{7}{4}, -210^{\circ})\)
    4. \(\ \text{D}(5, \frac{\pi}{2})\)
    5. \(\ \text{E}(3.5, \frac{-\pi}{8})\)

    Назвіть дві інші пари полярних координат для кожної точки.

    1. \(\ (1.5, 170^{\circ})\)
    2. \(\ (-5, \frac{\pi}{-3})\)
    3. \(\ (3, 305^{\circ})\)

    Графік кожного полярного рівняння.

    1. \(\ r=3\)
    2. \(\ \theta=\frac{\pi}{5}\)
    3. \(\ r=15.5\)
    4. \(\ r=1.5\)
    5. \(\ \theta=-175^{\circ}\)

    Знайти відстань між заданими точками.

    1. \(\ P_{1}\left(5, \frac{\pi}{2}\right) \text { and } P_{2}\left(7, \frac{3 \pi}{9}\right)\)
    2. \(\ P_{1}\left(1.3,-52^{o}\right) \text { and } P_{2}\left(-13.6,-162^{\circ}\right)\)
    3. \(\ P_{1}\left(3,250^{\circ}\right) \text { and } P_{2}\left(7,90^{\circ}\right)\)

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 4.1.

    Лексика

    Термін Визначення
    \(\ \pi\) \(\ \pi\)(Pi) - відношення окружності кола до його діаметру. Це ірраціональне число, яке приблизно дорівнює 3,14.
    Декартова система координат Декартова площина - це сітка, утворена горизонтальною цифровою лінією та вертикальною цифровою лінією, які перетинаються в точці (0, 0), яка називається початком.
    полярна вісь Полярна вісь - це промінь, проведений від полюса під кутом 0 на полярному графіку.
    полярна система координат Полярна система координат - це спеціальна система координат, в якій розташування кожної точки визначається її відстанню від полюса і кутом по відношенню до полярної осі.
    полюс Полюс - це центральна точка на полярному графіку.
    радіан Радіан - це одиниця кута, яка дорівнює куту, створеному в центрі кола, дуга якого по довжині дорівнює радіусу.

    Атрибуції зображень

    1. [Рисунок 1]
       Кредит: Невідоме
      джерело: https://es.Wikipedia.org/wiki/Archivo:Lahore-PIA-747-TakeOff-80375.JPG
    2. [Рисунок 2]
       Кредит: Невідоме
      джерело: https://es.Wikipedia.org/wiki/Archivo:Lahore-PIA-747-TakeOff-80375.JPG
    3. [Рисунок 3]
       Кредит: Невідоме
      джерело: https://es.Wikipedia.org/wiki/Archivo:Lahore-PIA-747-TakeOff-80375.JPG