Skip to main content
LibreTexts - Ukrayinska

4.4.2: Полярна та декартова трансформація

  1. Last updated
  2. Save as PDF
  • Page ID
    55010

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Полярна і декартова трансформація

    Під час цього уроку ви побачите, що точки можна перетворити з прямокутної форми в полярну форму за допомогою невеликої алгебри та тригонометрії.

    Чи можна також перетворити рівняння форми? Як щодо кола, наприклад?

    Полярна і декартова трансформація

    Полярна форма до прямокутної форми

    Іноді задається проблема з координатами в полярній формі, але може знадобитися прямокутна форма.

    Щоб перетворити\(\ \left(4, \frac{3 \pi}{4}\right)\) полярну точку в прямокутні координати: спочатку визначте (r, θ).

    \(\ r=4 \text { and } \theta=\frac{3 \pi}{4}\)

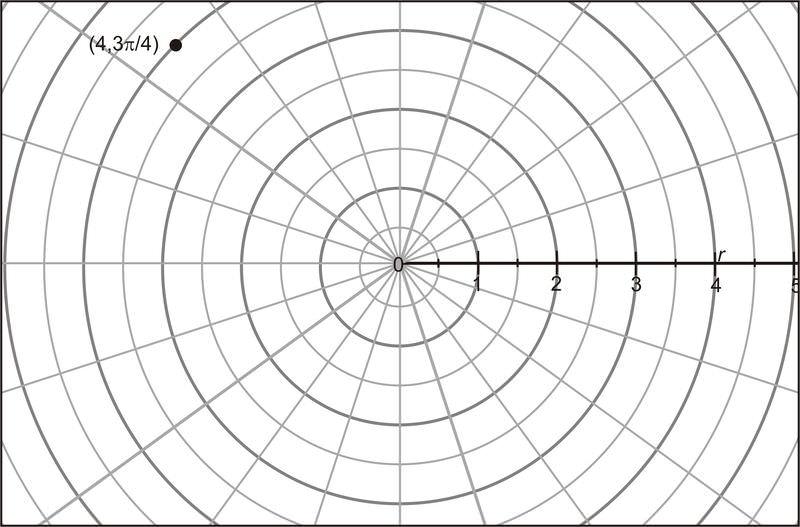
    Ф-Д_2Ф037 КБК 1С2 АДФ 267621965d18cd 0652510715622АААК 35А44Б8ЕА5+зображення_крихіткий+зображення_крихіткий.jpg

    По-друге, проведіть вертикальну лінію від точки до полярної осі (горизонтальної осі). Відстань від полюса до місця, де лінія, яку ви тільки що намалювали, перетинає полярну вісь, - це значення x, а довжина відрізка лінії від точки до полярної осі - значення y.

    Ці відстані можна обчислити за допомогою тригонометрії:

    х = r cos θ і у = r sin θ

    \(\ x=4 \cos \frac{3 \pi}{4} \text { and } y=4 \sin \frac{3 \pi}{4} \text { or } x=-2 \sqrt{2} \quad y=2 \sqrt{2}\)

    \(\ \left(4, \frac{3 \pi}{4}\right)\)в полярних координатах еквівалентно\(\ x=-2 \sqrt{2} \quad y=2 \sqrt{2}\)

    Прямокутна форма до полярної форми

    Перехід від прямокутних координат до полярних координат також можливий, але це вимагає трохи більше роботи. Припустимо, ми хочемо знайти полярні координати прямокутної точки (2, 2). Щоб почати виконувати цю операцію, відстань, яку точка (2, 2) знаходиться від початку (радіус, r), можна знайти за

    \ (\\ почати {масив} {л}
    r=\ sqrt {x^ {2} +y^ {2}}\\
    r=\ sqrt {2^ {2} +2^ {2}}\\
    r=\ sqrt {8} =2\ sqrt {2}
    \ кінець {масив}\)

    Кут, за яким відрізок лінії між точкою і початком може бути знайдений

    \ (\\ почати {масив} {л}
    \ тан\ тета=\ гідророзриву {y} {x}\
    \ тан\ тета =\ гідророзриву {2} {2}\\ тан
    \ тета = 1\\\ тета=
    \ тан ^ {-1} 1\\\
    theta=\ frac {\ pi} {4}
    \ кінець {масив}\)

    Оскільки ця точка знаходиться в першому квадранті (координати x і y позитивні), кут повинен бути\(\ 45^{\circ} \text { or } \frac{\pi}{4}\) радіанами. Можливо також, що при tan θ = 1 кут може бути в третьому квадранті, або\(\ \frac{5 \pi}{4}\) радіанах. Але цей кут не задовольнить умовам задачі, так як кут третього квадранта повинен мати і x, і y негативні.

    Примітка

    при використанні\(\ \tan \theta=\frac{y}{x}\) для пошуку міри θ слід спочатку розглянути частку\(\ \tan \theta=\left|\frac{y}{x}\right|\) і знайти перший кут квадранта, який задовольняє цій умові. Цей кут і буде називатися опорним кутом, позначається\(\ \theta_{\text {ref }}\). Знайдіть фактичний кут, аналізуючи, в якому квадранті кут повинен бути заданий знаками x і y.

    Приклади

    Приклад 1

    Раніше вас запитали, чи можна перетворити рівняння кола з прямокутної форми в полярну форму.

    Рішення

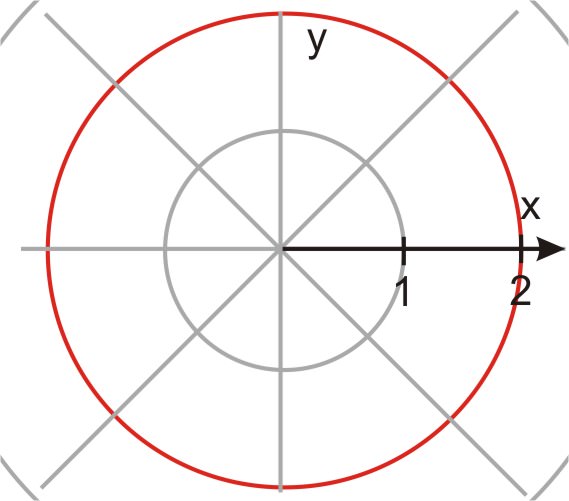
    Рівняння кола: x 2 + y 2 = k 2 - рівняння кола радіусом k в прямокутних координатах.

    Рівняння кола гранично просте в полярній формі. Насправді коло на полярному графіку є аналогом горизонтальної лінії на прямокутному графіку!

    Ви можете перетворити це рівняння в полярну форму, замінивши полярні значення на x, y. Нагадаємо х = r cos θ і у = r sin θ.

    (r cos θ) 2 + (r sin θ) 2 = к 2,

    квадратні члени: r 2 cos 2 θ + r 2 sin 2 θ = k 2,

    множник r 2 з обох членів зліва: r 2 (cos 2 θ + sin 2 θ) = k 2

    нагадати ідентичність: cos 2 θ + sin 2 θ = 1

    р 2 = к 2

    Отже: r = ± k - рівняння для кола в полярних одиницях.

    Коли r дорівнює константі, полярний графік - це коло.

    Ф-Д_4ФД4С980Ф9С6672Б76Е7Д59 САА АС 64CD61CEA78БФ5Д912Е24Б43458АА+зображення_крихіткий+зображення_крихіткий.jpg[Малюнок 1]
    Приклад 2

    Перетворіть полярні\(\ \left(2, \frac{11 \pi}{6}\right)\) координати на прямокутну форму.

    Рішення

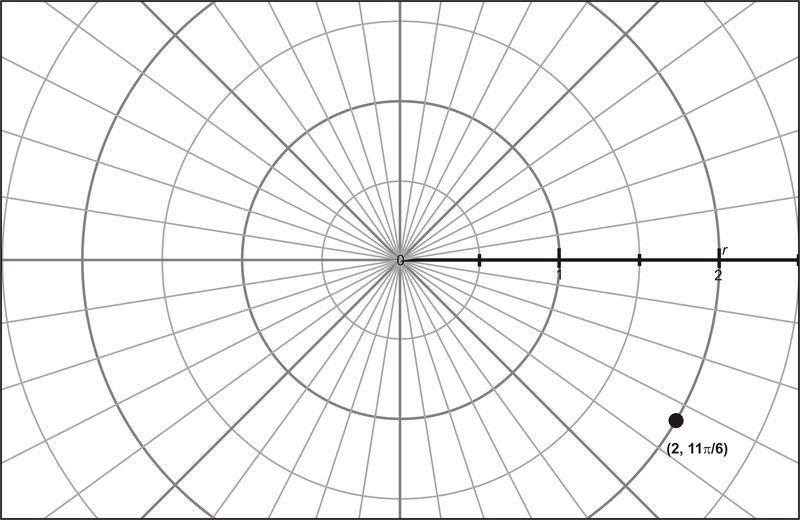
    Ф-Д_4627760Ф6Б74С76ФБ711Е2ДД4ДД1АД 3Д86 ДД209Е5Е5Ф84595Ф8А113ААБ+зображення_крихіткий+зображення_крихіткий.jpg

    \(\ r=2 \text { and } \theta=\frac{11 \pi}{6}\)

    \(\ x=r \cos \theta \text { and } y=r \sin \theta\)

    \(\ x=2 \cos \frac{11 \pi}{6} \text { and } y=2 \sin \frac{11 \pi}{6} \text { or } x=3 \sqrt{2} \quad y=-1\)

    \(\ \left(2, \frac{11 \pi}{6}\right)\)еквівалентно\(\ (3 \sqrt{2},-1)\) або в десятковій формі, приблизно (4.342, −1).

    Приклад 3

    Знайти полярні координати для\(\ (3,-3 \sqrt{3})\).

    Рішення

    \(\ x=3\)і\(\ y=-3 \sqrt{3}\)

    Намалюйте прямокутний трикутник в стандартній формі. Знайдіть відстань, яку точка знаходиться від початку, і кут відрізка лінії, який представляє цю відстань, складає з віссю +x:

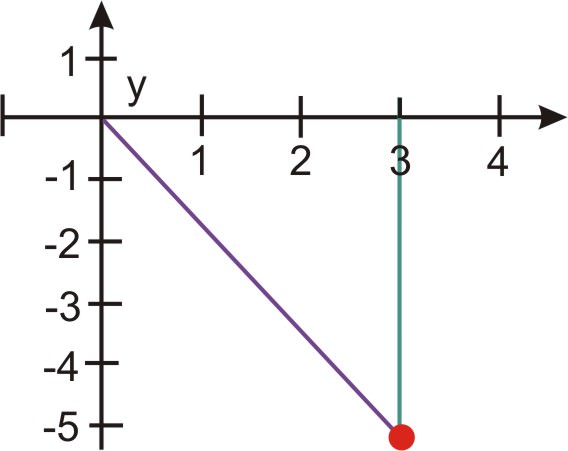    F-D_4093308 АФ БББ 1ДА26Б9 СБ534371Ф6Д77Ф93407312FF7559CE7656+зображення_крихіткий+зображення_крихіткий.jpg[Малюнок 2]

    \ (\\ почати {масив} {л}
    r=\ sqrt {3^ {2} + (-3\ sqrt {3}) ^ {2}}\\
    =\ sqrt {9+27}\
    =\ sqrt {36}\\
    =6
    \ end {масив}\)

    І за кутом,

    \ (\\ почати {масив} {л}
    \ тан\ тета_ {ref} =\ ліворуч |\ frac {(-3\ sqrt {3})} {3}\ праворуч |\\ tan
    \ theta_ {3}\\ theta_ {ref} =
    \ гідророзриву {\ pi} {3}
    \ end {масив}\)

    Отже,\(\ \theta_{r e f}=\frac{\pi}{3}\) і ми можемо подивитися на знаки x і y — (+, -) — щоб побачити це,\(\ \theta=\frac{5 \pi}{3}\) оскільки це кут четвертого квадранта.

    \(\ (3,-3 \sqrt{3})\)Прямокутна точка еквівалентна полярній точці\(\ \left(6, \frac{5 \pi}{3}\right)\).

    Нагадаємо, що при вирішенні для θ ми використовували

    \(\ \tan \theta=\left|\frac{(-3 \sqrt{3})}{3}\right|\)або\(\ \tan \theta=\sqrt{3}\)

    Ми знайшли

    \(\ \theta=\frac{5 \pi}{3}\). АЛЕ, також\(\ \theta\) може бути\(\ \theta=\frac{2 \pi}{3}\). Ви повинні вивчити знаки кожної координати, щоб побачити, що кут повинен бути в четвертому квадранті в прямокутних одиницях або між\(\ \frac{3 \pi}{2}\) і\(\ 2 \pi\) в полярних одиницях. З двох можливих кутів для\(\ \theta\), тільки\(\ \frac{5 \pi}{3}\) дійсний. Зверніть увагу, що при використанні tan -1 на калькуляторі ви завжди отримаєте відповідь в діапазоні\(\ -\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2}\).

    Приклад 4

    Перетворіть наступні прямокутні координати на полярні координати.

    1. \(\ (3,3 \sqrt{3})\)
    2. \(\ (−2,2)\)

    Перетворіть наступні полярні координати на прямокутні координати.

    1. \(\ \left(4, \frac{2 \pi}{3}\right)\)
    2. \(\ \left(-1, \frac{5 \pi}{6}\right)\)

    Рішення

    1. \(\ \left(6,66^{\circ}\right)\)
    2. \(\ \left(2 \sqrt{2}, 225^{\circ}\right)\)
    3. \(\ (-2,2 \sqrt{3})\)
    4. \(\ \left(\frac{\sqrt{3}}{2},-\frac{1}{2}\right)\)
    Приклад 5

    Висловіть рівняння в прямокутному вигляді: r=6cosθ.

    Рішення

    r 2 = 6rcosθ: помножити обидві сторони на r

    x 2+у 2 = 6x: Використання х 2+у 2 = r 2 та x = rcosθ

    x 2+y 2 = 6x - рівняння прямокутної форми.

    Приклад 6

    Висловіть рівняння в прямокутному вигляді: r=6.

    Рішення

    Цей простий:

    r=6 - полярна форма рівняння для кола

    r 2 = 6 2: квадрат з обох сторін

    x 2+y 2 = 36: Використання x 2+y 2 = r 2 та спрощення

    x 2+y 2 =36 - рівняння прямокутної форми.

    Рецензія

    1. Як точка з полярними координатами (5, π) представлена в прямокутних координатах?

    Покладіть кожну точку нижче в полярних координатах (r, θ). Потім запишіть прямокутні координати (x, y) для точки.

    1. \(\ \left(3,60^{\circ}\right)\)
    2. \(\ \left(-10, \frac{\pi}{3}\right)\)
    3. \(\ (15, \pi)\)

    Задано прямокутні координати (x, y). Для кожного питання: а) знайти дві пари полярних координат (r, θ), одну з r > 0, а іншу з r < 0. b) Висловити θ в радіанах і округлити до найближчих сотих.

    1. \(\ (5,-5)\)
    2. \(\ (0,10)\)
    3. \(\ (−8,6)\)

    Перетворіть кожне полярне рівняння на рівняння за допомогою прямокутних Визначте графік, і дайте приблизний ескіз або опис ескізу.

    1. \(\ \theta=\frac{\pi}{10}\)
    2. \(\ r=8\)
    3. \(\ r \sin \theta=7\)
    4. \(\ r \cos \theta=-3\)

    Перетворіть кожне прямокутне рівняння на рівняння за допомогою полярних Визначте графік, і дайте приблизний ескіз або опис ескізу.

    1. \(\ x^{2}+y^{2}-2 x=0\)
    2. \(\ y=\sqrt{3} x\)
    3. \(\ y=-5\)
    4. \(\ x y=15\)

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 4.2.

    Лексика

    Термін Визначення
    Тангенс Тангенс кута в прямокутному трикутнику - це величина, знайдена діленням довжини сторони, протилежної заданому куту, на довжину сторони, прилеглої до заданого кута.
    косинус Косинус кута в прямокутному трикутнику - це величина, знайдена діленням довжини сторони, прилеглої до даного кута, на довжину гіпотенузи.
    полярні координати Полярні координати описують розташування на сітці за допомогою полярної системи координат. Розташування кожної точки визначається її відстанню від полюса і його кутом по відношенню до полярної осі.
    полярна форма Полярна форма точки або кривої задається через r і θ і графікується на полярній площині.
    квадрант Квадрант - це одна четверта координатної площини. Чотири квадранти нумеруються за допомогою римських цифр I, II, III та IV, починаючи у верхньому правому куті та збільшуючись проти годинникової стрілки.
    Квадранти Квадрант - це одна четверта координатної площини. Чотири квадранти нумеруються за допомогою римських цифр I, II, III та IV, починаючи у верхньому правому куті та збільшуючись проти годинникової стрілки.
    прямокутні координати Точка записується за допомогою прямокутних координат, якщо вона записана через x і y і може бути побудована на декартовій площині.
    прямокутна форма Прямокутна форма точки або кривої задається через x і y і зображується на декартовій площині.
    синус Синус кута в прямокутному трикутнику - це величина, знайдена діленням довжини сторони, протилежної заданому куту, на довжину гіпотенузи.