1.5.4: Позначення для перетворень

Last updated

Oct 27, 2022
Save as PDF
- 1.5.3: Поєднання перетворень
- 1.6: Операції над функціями

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Точкові позначення та позначення функцій

При виконанні декількох перетворень дуже легко зробити невелику похибку. Особливо це актуально, коли намагаєшся робити кожен крок подумки. Точкове позначення є корисним інструментом для концентрації зусиль на одній точці і допомагає уникнути дрібних помилок.

Як би виглядав f (3x) +7 в точкових позначеннях і чому це корисно?

Використання позначення функцій та позначення точок

Перетворення може бути записано в позначеннях функцій і в точкових позначеннях. Функція позначення є дуже поширеним і практичним, оскільки дозволяє графікувати будь-яку функцію, використовуючи той самий базовий процес мислення, який потрібно для графування параболи у формі вершини.

Інший спосіб графіка функції полягає в перетворенні кожної точки по черзі. Цей метод добре працює, коли таблиця значень x, y доступна або легко ідентифікується з графіка.

По суті, він приймає кожну координату (x, y) і призначає нову координату на основі перетворення.

(x, y) ⟶ (новий х, новий у)

Це позначення називається точковим. Нова координата y є простою і безпосередньо з того, що відбувається поза межами f (x), оскільки f (x) — це лише інший спосіб запису y. Наприклад, f (x) →2f (x) −1 матиме нову координату y 2y−1.

Нова координата x складніша. Вона походить від скасування операцій, які впливають на x. Наприклад, f (x) →f (2x−1) матиме нову координату x $\ \frac{x+1}{2}$ .

Функція позначення і точкові позначення зображення перетворення «Горизонтальний зсув вправо три одиниці, вертикальний зсув вгору 4 одиниці» є

ф (х) →ф (х−3) +4

(х, у) → (х+3, у+4)

Зверніть увагу, що операції з x відрізняються.

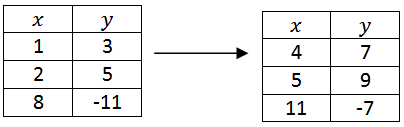
Застосуйте наведене вище перетворення до наступної таблиці пунктів.

х	у
1	3
2	5
8	−11

Зверніть увагу, що позначення точки значно зменшує ментальну візуалізацію, необхідну для збереження всіх перетворень відразу.

Приклади

Приклад 1

Рішення

Раніше вас запитали, якою буде функція f (3x) +7 при написанні в точкових позначеннях. Коли написано в точкових позначеннях, це буде написано як $\ (x, y) \rightarrow\left(\frac{x}{3}, y+7\right)$ . Це корисно, оскільки стає очевидним, що всі значення x діляться на три, а значення y збільшуються на 7.

Приклад 2

Перетворіть наступну функцію в точкових позначеннях в слова, а потім позначення функції.

(х, у) → (3х+1, −у+7)

Рішення

Горизонтальне розтягування в 3 рази, а потім горизонтальне зсув вправо на одну одиницю. Вертикальне відображення над віссю х і потім вертикальний зсув на 7 одиниць вгору.

$\ f(x) \rightarrow-f\left(\frac{1}{3} x-\frac{1}{3}\right)+7$

Приклад 3

Перетворіть наступні позначення функції в слова, а потім позначення точки. Нарешті, застосуйте трансформацію до трьох прикладних точок.

f (x) →−2f (х−1) +4

Рішення

Вертикальне відображення по осі x. Вертикальна розтяжка в 2 рази. Вертикальний зсув 4 од. Горизонтальний зсув вправо на одну одиницю.

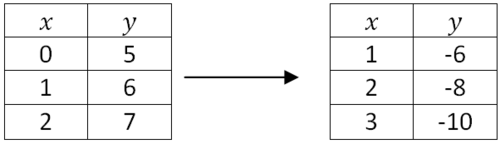
(x, y) → (x+1, −2y+4)

Приклад 4

Перетворіть наступні позначення функції в позначення точок і застосуйте його до включеної таблиці точок

$\ f(x) \rightarrow \frac{1}{4} f(-x-3)-1$

х	у
1	4
2	8

Рішення

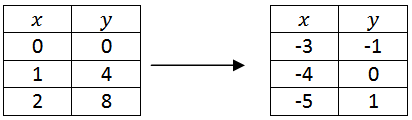
За y компонентом можна безпосередньо спостерігати. Для компонента x потрібно скасувати аргумент. $\ (x, y) \rightarrow\left(-x-3, \frac{1}{4} y-1\right)$

Приклад 5

Перетворіть наступні позначення точки на слова та функцію позначення, а потім застосуйте перетворення до включеної таблиці точок.

(x+3, y−1) → (2x+6, −y)

х	у
10	8
12	7
14	6

Рішення

Ця проблема інша, оскільки здається, що відбувається трансформація, що відбувається з початковою лівою точкою. Це додатковий шар виклику, оскільки трансформація інтересу - це лише різниця між двома пунктами. Зверніть увагу, що координата x просто подвоїлася, а координата y стала більшою на одиницю та стала негативною. Цю проблему можна переписати як:

(x, y) → (2x, − (y+1)) = (2x, −y−1)

$\ f(x) \rightarrow-f\left(\frac{x}{2}\right)-1$

Рецензія

х	у
	5
1	6
2	7

$\ f(x) \rightarrow-\frac{1}{2} f(x+1)$
г (х) →2г (3х) +2
h (x) →−h (x−4) −3
j (х) →3j (2х−4) +1
k (x) →−k (x−3)

Перетворіть наступні функції в точкових позначеннях в позначення функцій.

$\ (x, y) \rightarrow\left(\frac{1}{2} x+3, y-4\right)$
(x, y) → (2x+4, −y+1)
(x, y) → (4x,3y−5)
(2х, у) → (4x, −y+1)
(x+1, y−2) → (3x+3, −y+3)

Перетворіть наступні функції в позначенні функцій в точкові позначення.

ф (х) →3ф (х−2) +1
г (х) →−4г (х−1) +3
$\ h(x) \rightarrow \frac{1}{2} h(2 x+2)-5$
$\ j(x) \rightarrow 5 j\left(\frac{1}{2} x-2\right)-1$
$\ k(x) \rightarrow \frac{1}{4} k(2 x-4)$

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 1.3.

Лексика

Термін	Визначення
позначення функцій	У контексті перетворень позначення функції описує, як змінюється функція f (x) в результаті перетворення.
позначення точки	У контексті перетворень позначення точки описує, як змінюється кожна координата (x, y) в результаті перетворення.

Атрибуції зображень

[Рисунок 1]
Кредит: Фонд CK-12; Паула Еванс
Ліцензія: CC BY-SA
[Рисунок 2]
Кредит: Фонд CK-12; Паула Еванс
Ліцензія: CC BY-SA
[Рисунок 3]
Кредит: Фонд CK-12; Паула Еванс
Ліцензія: CC BY-SA
[Рисунок 4]
Кредит: Фонд CK-12; Паула Еванс
Ліцензія: CC BY-SA