1.5.2: Розтягування та відображення перетворень

Last updated

Oct 27, 2022
Save as PDF
- 1.5.1: Вертикальні та горизонтальні перетворення
- 1.5.3: Поєднання перетворень

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Розтягування та відображення перетворень

Розуміння того, як зміни рівняння функції призводять до розтягування та/або відображення графіка функції - це чудовий спосіб взяти частину таємниці з графіків більш складних рівнянь. Визнаючи сім'ю, до якої належить більш складне рівняння, а потім визначивши, які зміни були внесені до батька цієї сім'ї, графік навіть досить докладних функцій можна зробити набагато зрозумілішим.

Подивіться, чи можете ви визначити, які частини рівняння: $\ y=-\frac{1}{5} x^{2}$ представляють або розтягування, або відображення батьківської функції y=x ² перед прикладами в цьому розділі.

Розтягування та відображення перетворень

Розтягування та стиснення графіків

Якщо помножити функцію на коефіцієнт, графік функції буде розтягнутий або стиснутий.

З огляду на функцію f (x), ми можемо формалізувати стиснення і розтягування графа f (x) наступним чином:

Функція g (x) являє собою вертикальний розтяг f (x), якщо g (x) = cf (x) і c > 1.

Функція g (x) представляє вертикальне стиснення f (x), якщо g (x) = cf (x) і 0 < c < 1.

Функція h (x) являє собою горизонтальне стиснення f (x), якщо h (x) = f (cx) і c > 1.

Функція h (x) являє собою горизонтальний розтяг f (x), якщо h (x) = f (cx) і 0 < c < 1.

Зверніть увагу, що вертикальне стиснення або горизонтальне розтягнення відбувається, коли коефіцієнт є числом від 0 до 1.

Відображення графіків по осі Y та осі x

Розглянемо графіки функцій y = x ² і y = -x ², наведені нижче.

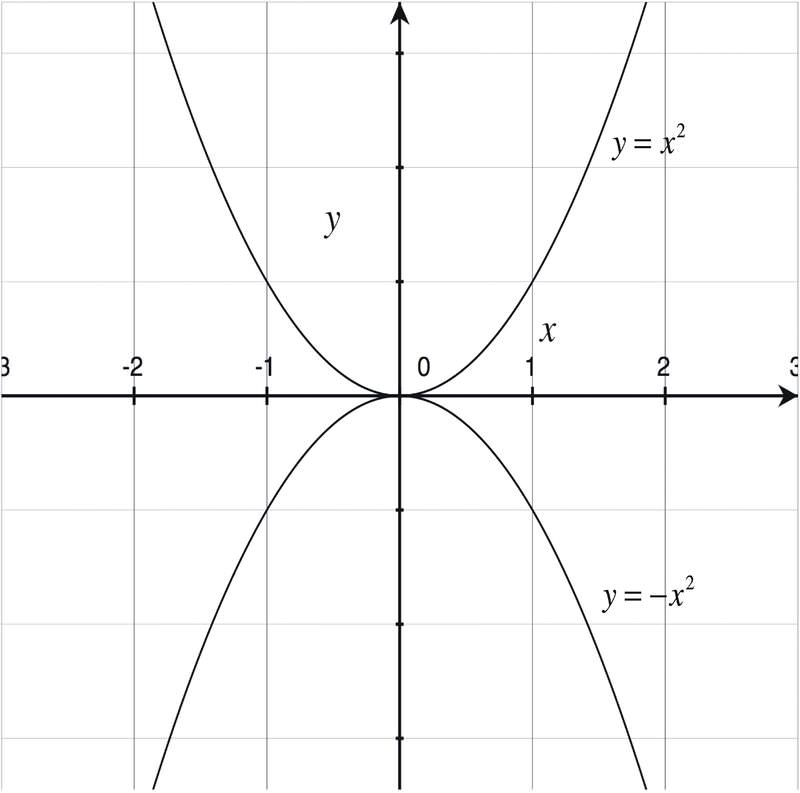
Ф-Д_Ф9957Е1А29С0С257Б07656096БА 5Ф6474Д1С31933217E5491769F5+зображення_крихіткий+зображення_крихіткий.jpg

Графік y = -x ² являє собою відображення y = x ², над віссю x. Тобто кожне значення функції y = -x ² є від'ємним значенням функції y = x ². Загалом, g (x) = -f (x) має графік, який є графом f (x), відображеним над віссю x.

Приклад 1

Рішення

Раніше вам задавали питання про виявлення перетворень.

Функція $\ y=-\frac{1}{5} x^{2}$ є результатом перетворення y = x ² шляхом відображення його над віссю x, через негативний коефіцієнт на x, і вертикального стиснення його (робить його ширшим), оскільки коефіцієнт на x - дріб між 0 і 1.

Приклад 2

Визначте графік функції y = (3x) ².

Рішення

Ми помножили х на 3. Це повинно вплинути на графік по горизонталі. Однак якщо спростити рівняння, то отримаємо y = 9x ². Тому графік, якщо ця парабола буде вищою/тонше, ніж y = x ². Множення x на число більше 1 створює горизонтальне стиснення, яке виглядає як вертикальна розтяжка.

Приклад 3

Визначте перетворення, описане y = ((1/2) x) ².

Рішення

Якщо спростити це рівняння, то отримаємо y = (1/4) х ². Тому множення x на число між 0 і 1 створює горизонтальне розтягування, яке виглядає як вертикальне стиснення. Тобто парабола буде коротше/ширше.

Приклад 4

Намалюйте графік y = x ³ і y = -x ³ на однакових осях.

Рішення

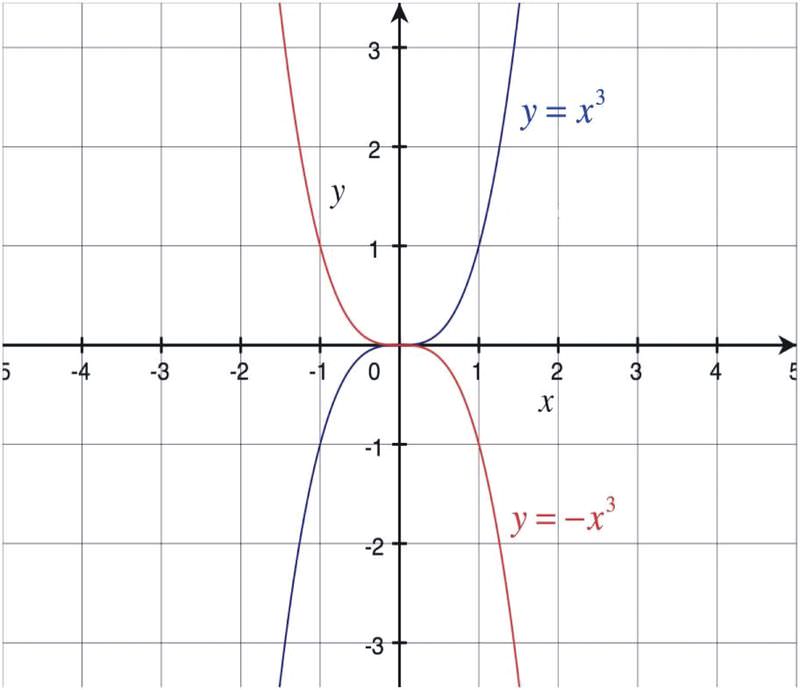
Ф-д_даффе 062279С80Е 719Е9019БФ0Д88Ф04ААААА 973Е5ЕЕЕЦ6БФ95+зображення_крихіткий+зображення_крихіткий.jpg

Спочатку дві функції можуть виглядати як дві параболи. Якщо ви графуєте вручну, або якщо ви встановите свій калькулятор в послідовний режим (а не одночасний), ви можете побачити, що графік y = -x ³ насправді є відображенням y = x ³ над віссю x.

Однак, якщо ви подивитеся на графік, ви можете побачити, що він є відображенням і над віссю Y. Так відбувається тому, що для того, щоб отримати відображення над віссю y, ми заперечуємо x Іншими словами, h (x) = f (-x) є відображенням f (x) над віссю y. Для функції у = х ³, h (x) = (-х) ³ = (-х) (-х) (-х) = -х ³. Це та сама функція, що і та, яку ми вже намалювали.

Важливо відзначити, що це особливий випадок. Графік y = x ² також є окремим випадком. Якщо ми хочемо відобразити y = x ² над віссю y, ми просто отримаємо той самий графік! Це можна пояснити алгебраїчно: у = (-х) ² = (-х) (-х) = х ².

Приклад 5

Графік функцій $\ y=\sqrt{x} \text { and } y=\sqrt{-x}$ .

Рішення

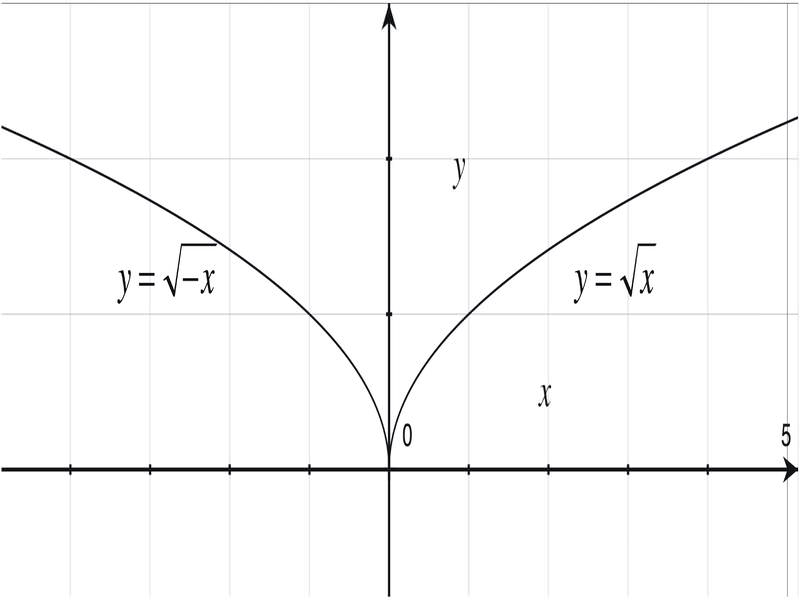
Рівняння $\ y=\sqrt{-x}$ може виглядати заплутаним через - x під квадратним коренем. Важливо мати на увазі, що - х означає протилежність х. Тому область цієї функції обмежена значеннями ≤ 0. Наприклад, якщо $\ x=-4, y=\sqrt{-(-4)}=\sqrt{4}=2$ . Саме ця область, яка включає всі дійсні числа, які не знаходяться в області $\ y=\sqrt{x}$ плюс нуль, дає нам графік, який є відображенням над віссю y.

У сумі графік представляє відображення над осі x, якщо функція була заперечена (тобто y була заперечена, якщо ми думаємо про y = f (x)). Графік являє собою відображення над віссю y, якщо змінна x була заперечена.

Ф-Д_АС 65С7 ЕД5Ф663Е983Ф7СБ3Б3А45Е8Ф6А88Е36Е20Е3Е1ДЦА2А+зображення_крихіткий+зображення_крихіткий.jpg

Приклад 6

Визначте функцію та намалюйте графік $\ y=\sqrt{x}$ відбитих по обох осях.

Рішення

Щоб відобразити графік $\ y=\sqrt{x}$ над обома осями, функція повинна бути заперечена як зовні, так і всередині кореня: $\ y=-\sqrt{-x}$ . Заперечення (негативне) зовні кореня має ефект відображення графіка по вертикалі, а заперечення всередині кореня відображає графік по горизонталі. На зображенні нижче показані три версії:

СИНІЙ: $\ y=\sqrt{x}$

ЗЕЛЕНИЙ: $\ y=-\sqrt{x}$

ЧЕРВОНИЙ: $\ y=\sqrt{-x}$

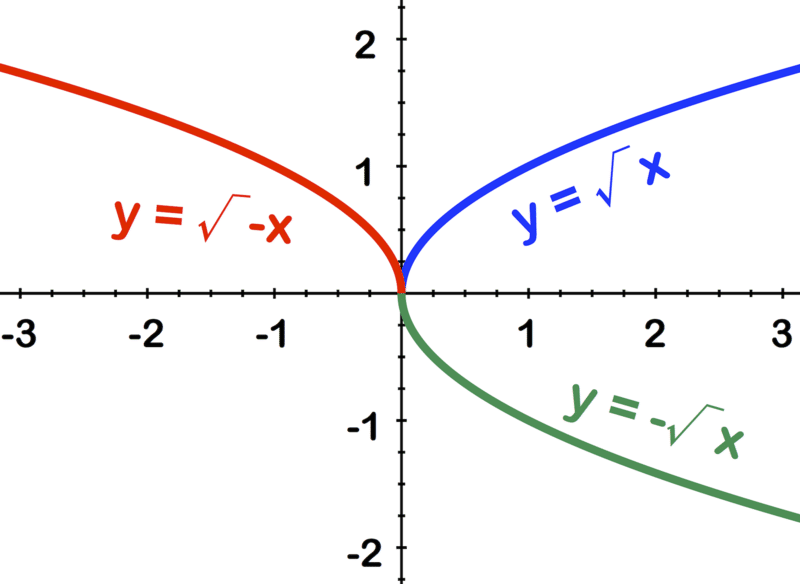
Ф-д_07а785А5БК85543А1А1 АА3ЕКА 302666588ФДБ77845БК084Б8ФЕ 32575D8+зображення_крихіткий+зображення_крихіткий.PNG

Рецензія

Якщо функцію помножити на коефіцієнт, що буде з графіком функції?
Що створює множення x на число більше одиниці?
Що відбувається, коли ми помножимо х на число між 0 і 1?
Для того, щоб отримати відображення над віссю y, що ми повинні зробити для x?
Як ми отримуємо відображення над віссю x?
Напишіть функцію, яка створить горизонтальне стиснення наступного:f (x) =x2+3
Напишіть функцію, яка буде горизонтально розтягувати наступне: f (x) =x ² −6
Перепишіть функцію, $\ f(x)=-\sqrt{x}$ щоб отримати відображення над віссю x.
Перепишіть функцію, $\ f(x)=\sqrt{x}$ щоб отримати відображення над віссю y.

Графік кожного з наступних за допомогою перетворень. Визначте переклади та роздуми.

f (x) =|х|−2
$\ h(x)=\sqrt{x+3}$
$\ g(x)=\frac{1}{x+1}$
f (x) =−4х ³
ч (х) = (х+3) ³ +1
$\ f(x)=\frac{1}{3}(x-3)^{2}+1$
$\ f(x)=-4 \sqrt{x+1}-2$
$\ f(x)=\frac{2}{3(x-2)}+\frac{1}{4}$

Нехай y=f (x) - функція, визначена відрізком лінії, що з'єднує точки (-1, 4) і (2, 5). Графік кожного з наступних перетворень y=f (x).

й=ф (х) +1
y=f (х+2)
y=f (−х)
y=f (х+3) −2

Графік y = x показаний нижче. Намалюйте графік кожного з наступних перетворень y = x

y=х+3
y=x−2
y=−x

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 1.13.

Лексика

Термін	Визначення
стиснення	Розтягування або стиснення - це перетворення функції, яке робить графік вужчим або ширшим, без перекладу його горизонтально або вертикально.
Функція сімейства	Сімейства функцій - це групи функцій з подібністю, які полегшують їх графік, коли ви знайомі з батьківською функцією, найпростішим прикладом форми.
батьківська функція	Батьківська функція - найпростіша форма певного типу функції. Всі інші функції цього типу зазвичай порівнюються з батьківською функцією.
Відображення	Відображення графіка означає перетворення графіка, щоб створити «дзеркальне відображення» вихідного графіка шляхом перегортання його через лінію.
Відображення	Відображення - це перетворення, які призводять до «дзеркального відображення» батьківської функції. Вони викликані різними ознаками між батьківськими і дочірніми функціями.
розтягнути	Розтяжка або стиснення - це перетворення функції, яке робить графік вужчим або ширшим.
розтягування	Розтягування графіка означає зробити графік вужчим або ширшим.
Трансформації	Перетворення використовуються для зміни графіка батьківської функції в граф більш складної функції.