Skip to main content
LibreTexts - Ukrayinska

1.1.3: Симетрія

  1. Last updated
  2. Save as PDF
  • Page ID
    55226

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Симетрія

    Деякі функції, такі як функція синуса, функція абсолютного значення та функція квадратури, мають симетрію відображення по лінії x = 0. Інші функції, такі як функція кубінгу та зворотна функція, мають обертальну симетрію щодо походження.

    Чому перша група класифікується як парні функції, тоді як друга група класифікується як непарні функції?

    Парні та непарні функції

    парні функції

    Функції, симетричні по лінії x=0 (вісь y), називаються парними. Навіть функції мають властивість, що коли від'ємне значення замінюється на x, воно створює те саме значення, що і при заміні додатного значення на x. Іншими словами, рівняння f (−x) =f (x) має значення true для парних функцій.

    Щоб показати, що функція f (x) =3x 4 −5x 2 +1 є парною, покажіть, що f (−x) =f (x).

    f (−x) =3 (−x) 4 −5 (−x) 2 +1

    = 3х 4 −5х 2 +1

    =ф (х)

    Властивість того, що як позитивні, так і негативні числа, підняті до парної сили, завжди позитивні, є причиною того, чому термін навіть використовується. При цьому не важливо, що коефіцієнти парні або непарні, тільки показники.

    Непарні функції

    Функції, які мають обертальну симетрію щодо походження, називаються непарними функціями. Непарні функції мають властивість, що коли в функцію підставляється від'ємне значення x, вона видає негативну версію функції, оціненої за додатним значенням. Іншими словами, рівнянняf (−x) =−f (x) має значення true для непарних функцій.

    Ця властивість стає все більш важливою у проблемах та доказах обчислення та за її межами, але наразі достатньо визначити функції, які є парними, непарними чи ні, і показати, чому.

    Щоб показати, що f (x) =4x 3 −x є непарним, покажіть, що f (−x) =−f (x).

    f (−x) =4 (−x) 3 −x

    =−4х 3+х

    =− (4х 3+х)

    =−f (х)

    Так само, як іменовані парні функції, непарні функції називаються, оскільки негативні ознаки не зникають і завжди можуть бути враховані з непарних функцій.

    Парні та непарні функції описують різні типи симетрії, але обидві вони отримують свою назву від властивостей показників. Негативне число, підняте до парного числа, завжди буде позитивним. Від'ємне число, підняте до непарного числа, завжди буде від'ємним.

    Приклади

    Приклад 1

    Які з основних функцій парні, які непарні, а які ні ні?

    Рішення

    Парні функції: Функція квадрата та функція абсолютного значення.

    Непарні функції: функція ідентичності, функція кубінгу, зворотна функція, функція синуса.

    Ні: функція квадратного кореня, експоненціальна функція та функція журналу. Логістична функція також не є ні тому, що вона обертально симетрична щодо точки (0,\(\ 1\over 2\)) на відміну від початку.

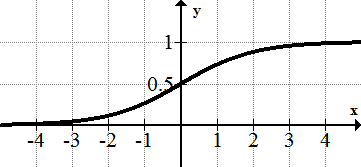    F-D_4503151956E3B3742D49327560551 DE2E49Ceda3B611B8A9DDCeb9A+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png[Малюнок 1]
    Приклад 2

    Припустимо, h (x) - парна функція, а g (x) - непарна функція. f (x) =h (x) +g (x). f (x) парний або непарний?

    Рішення

    Якщо h (x) навіть, то h (−x) =h (x). Якщо g (x) непарний, то g (−x) =−g (x).

    Отже: f (−x) =h (−x) +g (−x) =h (x) −g (x)

    Це не відповідає f (x) =h (x) +g (x) і не відповідає −f (x) =−h (x) −g (x).

    Це доказ, який показує суму парної функції, а непарна функція ніколи сама не буде парною або непарною.

    Приклад 3

    Визначте, чи є наступна функція парною, непарною чи ні.

    f (x) = х (х 2 −1) (х 4 +1)

    Визначте, чи функція парна, непарна чи ні, і поясніть, чому.

    Рішення

    f (x) = х (х 2 −1) (х 4 +1)

    f (−x) = (−x) ((−x) 2 −1) ((−x) 4 +1)

    =−х (х 2 −1) (х 4 +1)

    =−f (х)

    Функція є непарною, оскільки f (−x) =−f (x) має значення true.

    f (x) = 4х 3 −|х|

    f (−x) =4 (−x) 3 −x

    =−4x 3 −х

    Здається, це не відповідає ні f (x) =4x 3 −|x|, ні −f (x) =−4x 3 +|x|. Тому ця функція не є ні парною, ні непарною.

    Примітка

    Ця функція є різницею непарної функції і парної функції. Це повинно бути підказкою, що результуюча функція не є ні парною, ні непарною.

    Рецензія

    Визначте, чи є наступні функції парними, непарними чи ні.

    1. ф (х) =−4х 2 +1

    2. г (х) = 5х 3 −3х

    3. ч (х) = 2х 2 −х

    4. j (х) = (х−4) (х−3) 3

    5. к (х) = х (х2−1) 2

    6. ф (х) = 2х 3 −5х 2 −2х+1

    7. г (х) = 2х 2 −4х+2

    8. год (х) =−5х 4 +х 2 +2

    9. Припустимо, h (x) парне, а g (x) непарне. Показати, що f (x) =h (x) −g (x) не є ні парним, ні непарним.

    10. Припустимо, h (x) парне, а g (x) непарне. Покажіть, що\(\ f(x)=\frac{h(x)}{g(x)}\) непарно.

    11. Припустимо, h (x) парне, а g (x) непарне. Показати, що f (x) =h (x) ⋅g (x) непарне.

    12. Чи завжди сума двох парних функцій є парною функцією? Поясніть.

    13. Чи завжди сума двох непарних функцій є непарною функцією? Поясніть.

    14. Чому деякі функції ні парні, ні непарні?

    15. Якщо ви знаєте, що функція парна або непарна, що це говорить вам про симетрію функції?

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 1.6.

    Лексика

    Термін Визначення
    парна функція Парна функція - це функція з графом, який є симетричним відносно осі y і має властивість f (−x) =f (x).
    симетрія відображення Фігура має симетрію відображення, якщо вона може бути відображена через лінію і виглядати точно так само, як це було до відображення.
    Симетрія обертання Фігура має обертальну симетрію, якщо її можна повернути менше 360навколо своєї центральної точки і виглядати точно так само, як і до обертання.

    Атрибуції зображень

    1. [Малюнок 1]
       Кредит: Фонд CK-12; Паула Еванс; Роб Янг
      Джерело: https://www.flickr.com/photos/rob-young/1149735229/; https://commons.wikimedia.org/wiki/File:Will_%26_Grace_Apartment _Будівний_ (1149735229) .jpg
      Ліцензія: CC BY-SA; CC BY-NC-SA