Skip to main content
LibreTexts - Ukrayinska

12.6: Припинення держав

  1. Last updated
  2. Save as PDF
  • Page ID
    52951

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Хоча ми визначили, що наші машини зупиняються лише тоді, коли немає інструкції для виконання, загальні уявлення машин Тьюринга мають спеціальний стан зупинки\(h\), такий, що\(h \in Q\).

    Ідея, що стоїть за станом зупинки, проста: коли машина закінчила операцію (вона готова прийняти вхід або закінчила писати вихід), вона переходить у стан,\(h\) коли він зупиняється. Деякі машини мають два стани зупинки, один, який приймає вхід і той, який відхиляє введення.

    Приклад\(\PageIndex{1}\)

    Припинення держав. Щоб з'ясувати це поняття, почнемо з переробки парної машини. Замість того, щоб машина зупинялася в стані,\(q_0\) якщо вхід рівний, ми можемо додати інструкцію для відправки машини в стан зупинки.

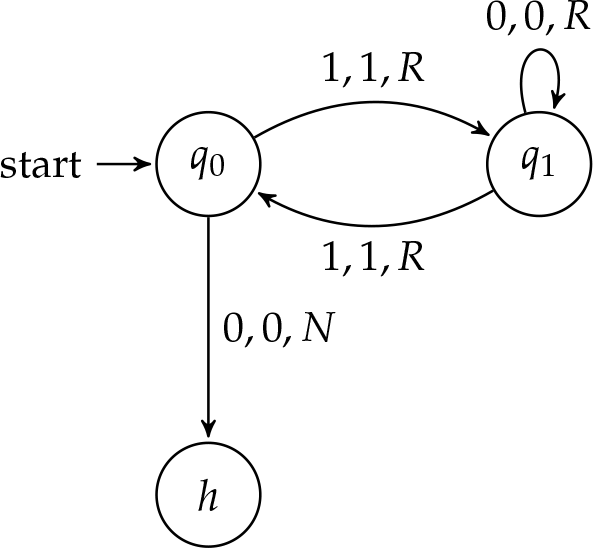
    12.6.1_навіть приховання.png

    Розширимо далі приклад. Коли машина визначає, що вхід непарний, він ніколи не зупиняється. Ми можемо змінити машину, щоб включити стан відхилення, замінивши інструкцію циклу інструкцією переходу до стану відхилення\(r\).

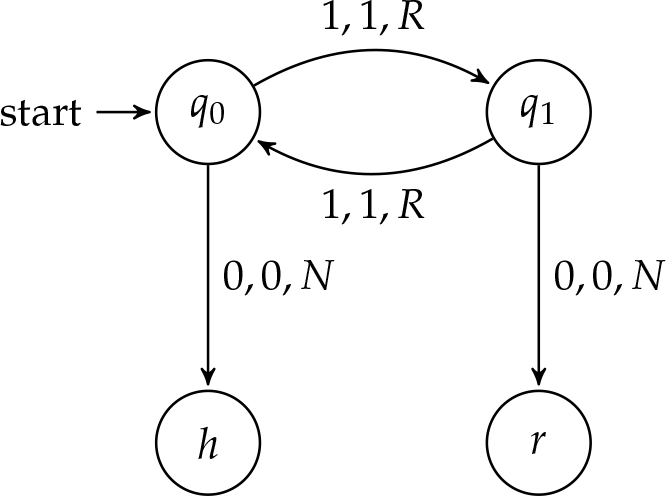
    12.6.2_навіть відкинути.png

    Додавання виділеного стану зупинки може бути вигідним у таких випадках, коли це робить явним, коли машина приймає/відхиляє певні входи. Однак важливо зазначити, що жодна обчислювальна потужність не отримується шляхом додавання виділеного стану зупинки. Аналогічно, менш формальне поняття зупинки має свої переваги. Визначення зупинки, яке використовується до цих пір в цьому розділі, робить доказ проблеми зупинки інтуїтивно зрозумілим і легким для демонстрації. З цієї причини ми продовжуємо наше початкове визначення.