12.7: Поєднання машин Тьюринга

Last updated
Save as PDF

Page ID: 52982

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Приклади машин Тьюринга, які ми бачили досі, були досить простими за своєю природою. Але насправді будь-яка проблема, яку можна вирішити будь-яким сучасним мовою програмування, також може бути вирішена за допомогою машин Тьюринга. Щоб побудувати більш складні машини Тьюринга, важливо переконати себе, що ми можемо їх комбінувати, щоб ми могли будувати машини для вирішення більш складних проблем, розбиваючи процедуру на простіші частини. Якщо ми зможемо знайти природний спосіб розбити складну проблему на складові частини, ми можемо вирішити проблему в кілька етапів, створивши кілька простих машин Тьюринга і об'єднавши їх в одну машину, яка може вирішити проблему. Цей момент особливо важливий при вирішенні проблеми зупинки в наступному розділі.

Приклад\(\PageIndex{1}\)

Поєднання машин: Створіть машину, яка обчислює функцію\(f(m,n) = 2(m+n)\).

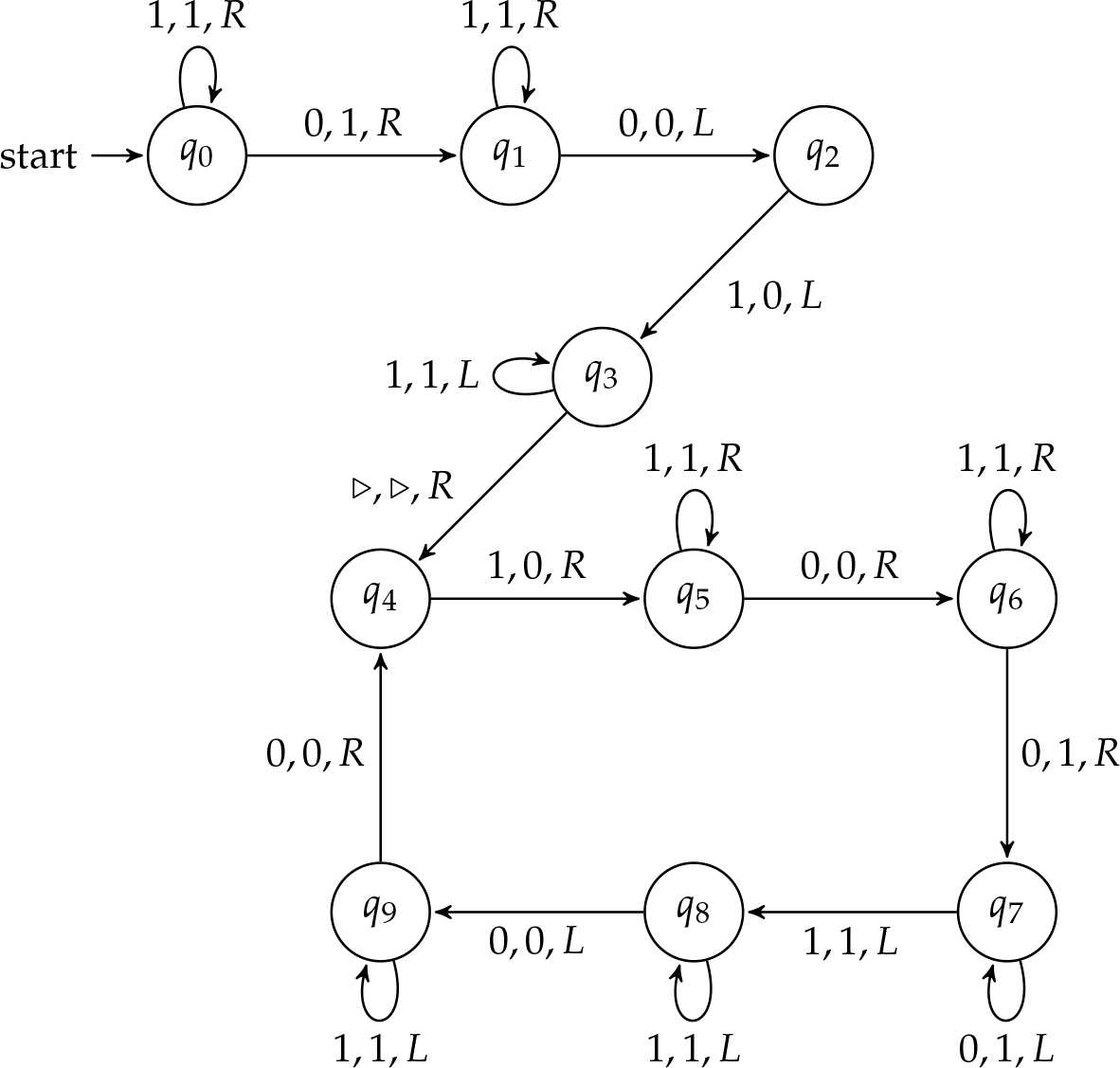
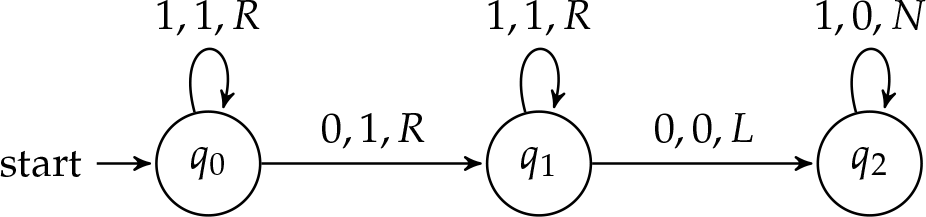
Для того, щоб побудувати цю машину, ми можемо об'єднати дві машини, з якими ми вже знайомі: машина додавання та дублер. Починаємо з малювання схеми стану машини складання.

12.7.1_дод.png

Замість зупинки в стані\(q_2\), ми хочемо продовжити роботу, щоб подвоїти вихід. Нагадаємо, що машина дублер стирає перший штрих на вході і записує два штрихи в окремий висновок. Давайте додамо інструкцію, щоб переконатися, що головка стрічки читає перший хід виходу машини додавання.

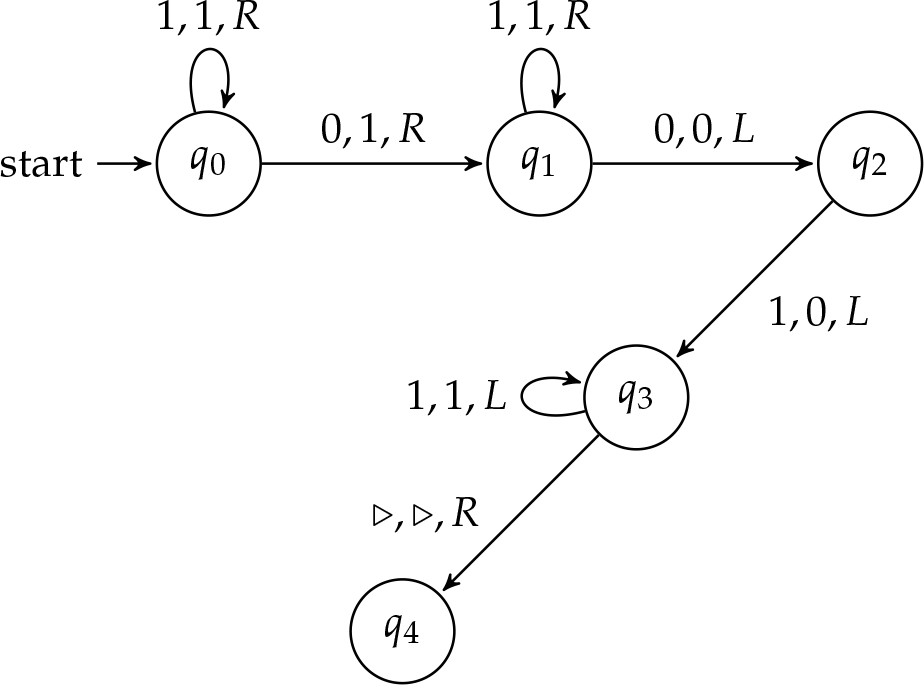
12.7.2_модифікувати.png

Тепер легко подвоїти вхід - все, що нам потрібно зробити, це підключити машину подвійника до стану\(q_4\). Це вимагає перейменування станів машини подвійника, щоб вони починалися\(q_4\) замість\(q_0\) —таким чином ми не закінчуємо двома початковими станами. Остаточна схема повинна виглядати так, як на малюнку\(\PageIndex{1}\).

**Малюнок\(\PageIndex{1}\):** Поєднання суматора і дублер машин