12.5: Унарне представлення чисел

Last updated
Save as PDF

Page ID: 52952

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Template:MathJaxZach

Машини Тьюринга працюють над послідовностями символів, написаних на їх стрічці. Залежно від алфавіту, який використовує машина Тьюринга, ці послідовності символів можуть представляти різні входи та виходи. Особливий інтерес, звичайно, представляють машини Тьюринга, які обчислюють арифметичні функції, тобто функції натуральних чисел. Простий спосіб представлення позитивних цілих чисел - це кодування їх як послідовності одного символу$\TMstroke$. Якщо$n \in \Nat$,$\TMstroke^n$ нехай порожня послідовність if$n = 0$, а в іншому випадку послідовність, що складається з точно$n$$\TMstroke$ 's.

Визначення$\PageIndex{1}$: Computation

Машина Тьюринга$M$ обчислює функцію,$f\colon \Nat^n \to \Nat$ якщо$M$ зупиняється на вході\[\TMstroke^{k_1} \TMblank \TMstroke^{k_2} \TMblank \dots \TMblank \TMstroke^{k_n}\nonumber\] з виходом$\TMstroke^{f(k_1, \dots, k_n)}$.

Приклад$\PageIndex{1}$

Додаток: Створіть машину, яка, коли задано вхідні дані двох непорожніх$\TMstroke$ рядків довжини$n$ та$m$, обчислює функцію$f(n,m) = n + m$.

Ми хочемо придумати машину, яка починається з двох блоків штрихів на стрічці і зупиняється одним блоком штрихів. Для початку нам знадобиться метод для виконання. Вхідні штрихи відокремлюються порожнім, тому одним із способів було б написати обведення на квадраті, що містить порожній, і стерти перший (або останній) штрих. Це призведе до блоку з$n + m$$\TMstroke$. Крім того, ми могли б діяти аналогічно машині подвійника, стираючи штрих з першого блоку і додаючи один до другого блоку штрихів, поки перший блок не буде повністю вилучено. Приступимо до колишнього прикладу.

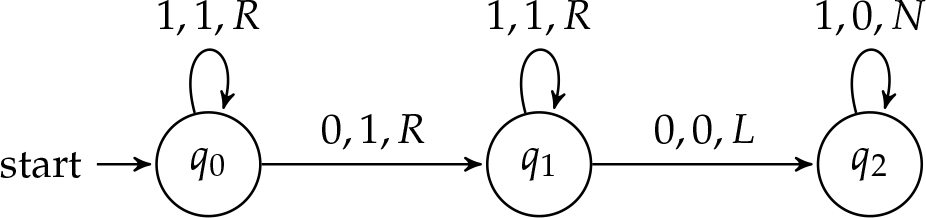
12.5.1_додаткова машина.png

Проблема$\PageIndex{1}$

Трасування через конфігурації машини для введення$\tuple{3,5}$.

Проблема$\PageIndex{2}$

Віднімання: Спроектуйте машину Тьюринга, яка при вході двох непорожніх рядків довжини$n$ і$m$$n > m$, де, обчислює функцію$f(n,m) = n - m$.

Проблема$\PageIndex{3}$

Рівність: Створіть машину Тьюринга для обчислення наступної функції:\[\fn{equality}(x,y) = \begin{cases} \text{1} & \text{if $x = y$} \\ \text{0} & \text{if $x \neq y$} \end{cases}\nonumber\] де$x$ і$y$ є цілими числами більше ніж$0$.

Проблема$\PageIndex{4}$

Спроектуйте машину Тьюринга для обчислення функції,$\min(x,y)$ де$x$ і$y$ є додатними цілими числами, представленими на стрічці рядками з$\TMstroke$ розділеними a$\TMblank$. Ви можете використовувати додаткові символи в алфавіті машини.

Функція$\min$ вибирає найменше значення зі своїх аргументів$\min(3,5)=3$, так$\min(20,16)=16$, і$\min(4,4)=4$, і так далі.