8.9: Вихідність і послідовність

Last updated
Save as PDF

Page ID: 52944

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Template:MathJaxZach

Зараз ми встановимо ряд властивостей відношення похідності. Вони самостійно цікаві, але кожен зіграє свою роль в доведенні теореми про повноту.

Пропозиція\(\PageIndex{1}\)

Якщо\(\Gamma \Proves A\) і\(\Gamma \cup \{A\}\) є непослідовним, то\(\Gamma\) непослідовно.

Доказ. Є кінцеві\(\Gamma_0\) і\(\Gamma_1 \subseteq \Gamma\) такі, що\(\Log{LK}\) виводить\(\Gamma_0 \Sequent A\) і\(A, \Gamma_1 \Sequent \quad\). Нехай\(\Log{LK}\) -виведенням\(\Gamma_0 \Sequent A\) бути\(\pi_0\) і\(\Log{LK}\) -виведенням\(\Gamma_1, A \Sequent \quad\) бути\(\pi_1\). Потім ми можемо вивести

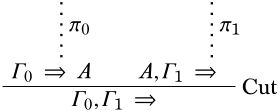
8.9.1.png

Так як\(\Gamma_0 \subseteq \Gamma\) і\(\Gamma_1 \subseteq \Gamma\)\(\Gamma_0 \cup \Gamma_1 \subseteq \Gamma\), отже,\(\Gamma\) непослідовно. ◻

Пропозиція\(\PageIndex{2}\)

\(\Gamma \Proves A\)iff\(\Gamma \cup \{\lnot A\}\) є непослідовним.

Доказ. По-перше\(\Gamma \Proves A\), припустимо, тобто є\(\pi_0\) виведення\(\Gamma \Sequent A\). Додавши\(\LeftR{\lnot}\) правило, отримуємо виведення\(\lnot A, \Gamma \Sequent \quad\), тобто\(\Gamma \cup \{\lnot A\}\) є непослідовним.

Якщо\(\Gamma \cup \{\lnot A\}\) є непослідовним, відбувається\(\pi_1\) виведення\(\lnot A, \Gamma \Sequent \quad\). Нижче наведено виведення\(\Gamma \Sequent A\):

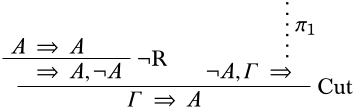
8.9.2.png

◻

Проблема\(\PageIndex{1}\)

Доведіть, що\(\Gamma \Proves \lnot A\) iff\(\Gamma \cup \{A\}\) є непослідовним.

Пропозиція\(\PageIndex{3}\)

Якщо\(\Gamma \Proves A\) і\(\lnot A \in \Gamma\), то\(\Gamma\) непослідовно.

Доказ. Припустимо\(\Gamma \Proves A\), і\(\lnot A \in \Gamma\). Потім відбувається виведення\(\pi\) послідовності\(\Gamma_0 \Sequent A\). \(\lnot A, \Gamma_0 \Sequent \quad\)Послідовність також виводиться:

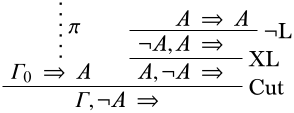
8.9.3.png

Оскільки\(\lnot A \in \Gamma\) і\(\Gamma_0 \subseteq \Gamma\), це показує, що\(\Gamma\) є непослідовним. ◻

Пропозиція\(\PageIndex{4}\)

Якщо\(\Gamma \cup \{A\}\) і\(\Gamma \cup \{\lnot A\}\) обидва несумісні,\(\Gamma\) то суперечливі.

Доказ. Існують кінцеві\(\Gamma_0 \subseteq \Gamma\)\(\Gamma_1 \subseteq \Gamma\) множини і\(\Log{LK}\) -похідні\(\pi_0\) і\(\pi_1\) з\(A, \Gamma_0 \Sequent \quad\) і\(\lnot A, \Gamma_1 \Sequent \quad\), відповідно. Потім ми можемо вивести

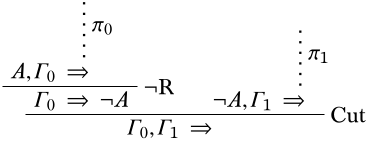
8.9.4.png

Так як\(\Gamma_0 \subseteq \Gamma\) і\(\Gamma_1 \subseteq \Gamma\),\(\Gamma_0 \cup \Gamma_1 \subseteq \Gamma\). Отже\(\Gamma\), непослідовно. ◻