5.4: Тестування еволюційних кореляцій
Існує багато способів перевірити еволюційні кореляції між двома символами. Традиційні методи, такі як PIC та PGLS, чудово працюють для тестування еволюційної регресії, яка дуже схожа на тестування еволюційних кореляцій. Однак при використанні цих методів зв'язок з реальними моделями еволюції характеру може залишатися непрозорим. Таким чином, я вперше представлю підходи до тестування корельованої еволюції на основі вибору моделі за допомогою АПК та Байєсівського аналізу. Потім я повернуся до «стандартних» методів еволюційної регресії в кінці глави.
Розділ 5.4a: Тестування кореляцій символів з використанням максимальної ймовірності та AIC
Щоб перевірити еволюційну кореляцію між двома символами, нас дійсно цікавлять елементи в матриці R. Для двох символів, x і y, R можна записати як:
(ур. 5,8)
R=[σ2xσxyσxyσ2y]
Нас цікавить параметр σ x y - еволюційна коваріація - і дорівнює він нулю (без кореляції) чи ні. Один простий спосіб перевірити цю гіпотезу - встановити дві конкуруючі гіпотези і порівняти їх між собою. Одна гіпотеза (H 1) полягає в тому, що риси еволюціонують незалежно один від одного, а інша (H 2), що риси розвиваються з деякою коваріацією σ x y. Ми можемо записати ці дві матриці швидкості як:
(ур. 5,9)
RH1=[σ2x00σ2y]RH2=[σ2xσxyσxyσ2y]
Ми можемо обчислити оцінку ML параметрів в R H 2 за допомогою рівняння 5.4. Оцінку максимальної ймовірності R H 1 можна отримати, зазначивши, що, якщо еволюція характеру незалежна по всіх символах, то і σ x 2, і σ y 2 можна отримати, обробляючи кожен символ окремо і використовуючи рівняння з глави 3 для вирішення для кожного. Виходить, що оцінки МЛ для σ х 2 і σ у 2 завжди точно однакові для Н 1 і Н 2.
Щоб порівняти ці дві моделі, ми обчислимо ймовірність кожної з них, використовуючи рівняння 5.4. Потім ми можемо порівняти ці дві ймовірності, використовуючи або тест на коефіцієнт ймовірності, або порівнявши бали AiCC (див. Розділ 2).
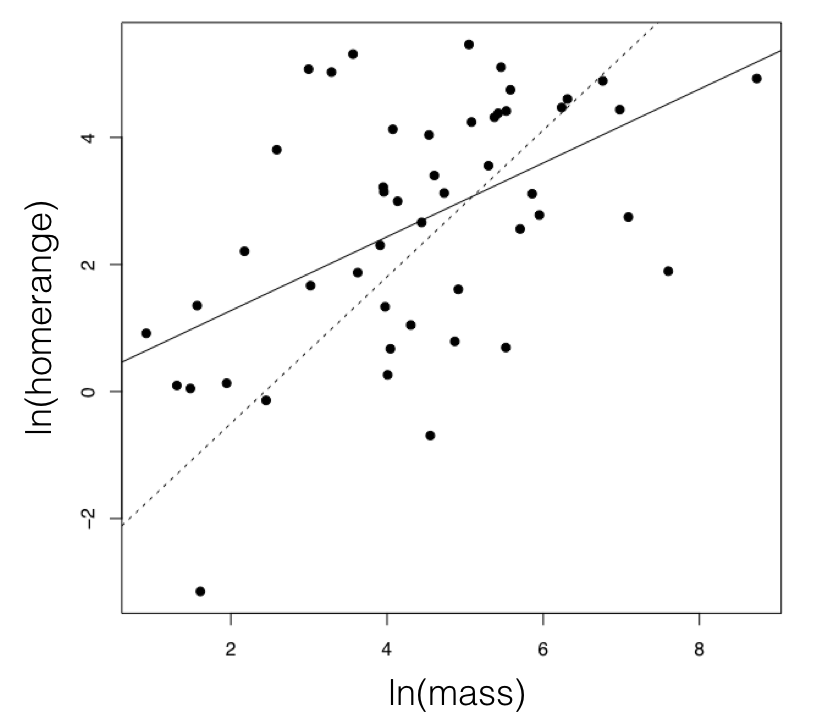
Для прикладу ссавців ми можемо розглянути дві риси (ln-трансформованого) розміру тіла та розміру домашнього діапазону (Garland 1992). Ці два символи мають позитивну кореляцію за допомогою стандартного регресійного аналізу (r = 0,27), а лінійна регресія значна (P = 0,0001; рис. 5.3). Якщо ми підходимо до цих даних багатовимірну броунівську модель руху, розглядаючи домашній діапазон як ознаку 1, а масу тіла як ознаку 2, то отримаємо наступні оцінки параметрів:
(ур. 5,10)
ˆaH2=[2.544.64]ˆRH2=[0.240.100.100.09]
Зверніть увагу на позитивний позадіагональний елемент в оцінюваній матриці R, що свідчить про позитивну еволюційну кореляцію між цими двома ознаками. Ця модель відповідає гіпотезі 2 вище і має log-ймовірність l n L = −164,0. Якщо ми підходимо до моделі без кореляції між двома ознаками, ми отримаємо:
(ур. 5,11)
ˆaH1=[2.544.64]ˆRH1=[0.24000.09]
Варто ще раз зазначити, що це модельне обмеження вплинуло лише на оцінки еволюційної кореляції; всі інші оцінки параметрів залишаються колишніми. Ця модель має меншу (більш негативну) вірогідність журналу l n L = −180,5.
Тест на коефіцієнт ймовірності дає Δ = 33,0, а P < <0,001, відкидаючи нульову гіпотезу. Різниця в оцінках A I C дорівнює 30.9, а вага Akaike для моделі 2 фактично дорівнює 1.0. Всі способи порівняння цих двох моделей дають сильну підтримку гіпотезі 2. Можна зробити висновок, що існує еволюційна кореляція між масою тіла та розмірами домашнього ареалу у ссавців. Що це означає в еволюційному плані, це те, що у ссавців еволюційні зміни маси тіла, як правило, позитивно коваріюються зі змінами домашнього діапазону.
Розділ 5.4b: Тестування кореляцій символів за допомогою вибору моделі Байєса
Ми також можемо реалізувати байєсійський підхід до тестування корельованої еволюції двох символів. Найпростіший спосіб зробити це - лише використовувати стандартний алгоритм Байєсівського MCMC, щоб відповідати корельованій моделі до двох символів. Ми можемо змінити алгоритм, представлений у розділі 2, наступним чином:
- Зразок множини значень початкових параметрів σ x 2, σ y 2, σ x y, $\ bar {z} _1 (0) $ та $\ bar {z} _2 (0) $ з попередніх розподілів. Для цього прикладу ми можемо встановити наш попередній розподіл як рівномірний між 0 та 1 для σ x 2 та σ y 2, рівномірний від -1 до +1 для σ x y, рівномірний від 1 до 9 для $\ bar {z} _1 (0) $ (lNMass), і -3 до 5 для $\ bar {z} _1 (0) $ (lnHomeRange).
- Враховуючи поточні значення параметрів, виберіть нові запропоновані значення параметрів за допомогою густини пропозиції Q (p ′| p). Тут для всіх п'яти значень параметрів ми будемо використовувати рівномірну густину пропозиції шириною 0,2, так що Q (p ′| p) U (p − 0,1, p + 0,1).
- Обчисліть три співвідношення:
- Коефіцієнт попереднього коефіцієнта, R p r i o r. Це відношення ймовірності витягування значень параметрів p і p' від попереднього. Оскільки наші попередні рівні однорідні, R p r i o r = 1.
- Пропозиція коефіцієнт щільності, R p r o p o s a l. Це співвідношення ймовірності пропозицій, що йдуть від p до p' і зворотного. Наша щільність пропозиції симетрична, так що Q (p ′| p) = Q (p | p ′) і R p r o p o s a l = 1.
- Коефіцієнт ймовірності, R l i k e l i h o o d. Це співвідношення ймовірностей даних з урахуванням двох різних значень параметрів. Ми можемо обчислити ці ймовірності з рівняння 5.6 вище (ур. 5.12).
\ [R_ {ймовірність} =\ розриву {L (P'|д)} {L (p|d)} =\ розриву {P (D|p ')} {P (D|р)}\ [
- Знайдіть R a c c e p t, добуток попередніх коефіцієнтів, коефіцієнт щільності пропозиції та коефіцієнт ймовірності. У цьому випадку як попередні коефіцієнти, так і коефіцієнти щільності пропозиції дорівнюють 1, тому R a c c e p t = R l i k e l i ч о о д.
- Намалюйте випадкове число x з рівномірного розподілу між 0 і 1. Якщо x < R a c c e p t, прийміть запропоноване значення всіх параметрів; в іншому випадку відхиліть і збережіть поточні значення параметрів.
- Повторіть кроки 2-5 велику кількість разів.
Потім ми можемо перевірити задній розподіл для параметра значно більше (або менше) нуля. Як приклад, я запустив цей MCMC протягом 100 000 поколінь, відкинувши перші 10 000 поколінь як спалювання. Потім я вибрав задній розподіл кожні 100 поколінь і отримав такі оцінки параметрів: $\ hat {\ sigma} _x^2 = 0,26$ [95% достовірний інтервал (СІ): 0,18 - 0,38], $\ hat {\ sigma} _y^2 = 0,10$ (95% CI: 0,06 -0,15) та $\ hat {\ sigma} _ {xy} = 0,11$ (95% CI: 0,06 -0,15) та $\ hat {\ sigma} _ {xy} = 0,11$ (95% CI: 0,06 -0,15) КІ: 0,06 - 0,17; див. Рис. 5.4). Ці результати можна порівняти з нашими оцінками ML. Крім того, 95% CI для σ x y не перекривається з 0; насправді жоден із 901 задніх зразків σ х y не менше нуля. Знову ж таки, можна з упевненістю зробити висновок, що між цими двома персонажами існує еволюційна кореляція.
Розділ 5.5c: Тестування кореляцій символів за допомогою традиційних підходів (PIC, PGLS)
Викладений вище підхід, який перевіряє еволюційну кореляцію між персонажами за допомогою вибору моделі, зазвичай не застосовується в літературі порівняльної біології. Натомість більшість тестів кореляції характеру покладаються на філогенетичну регресію, використовуючи один з двох методів: філогенетичні незалежні контрасти (PIC) та філогенетичні загальні найменші квадрати (PGLS). PGLS насправді математично ідентичний PIC у простому випадку, описаному тут, і більш гнучкий, ніж PIC для інших моделей і типів символів. Тут я розгляну як PIC, так і PGLS і поясню, як вони працюють і як вони пов'язані з моделями, описаними вище.
Філогенетичні незалежні контрасти можуть бути використані для проведення регресійного тесту на зв'язок між двома різними персонажами. Для цього обчислюється стандартизовані PIC для ознаки x та ознаки y. Потім використовується стандартна лінійна регресія, примусова через походження, щоб перевірити зв'язок між цими двома наборами PIC. Необхідно змусити регресію через початок, оскільки напрямок віднімання контрастів у будь-якому вузлі дерева є довільним; відображення всіх контрастів по обох осях одночасно не повинно впливати на аналіз 3.
Для домашнього діапазону та маси тіла ссавців тест на регресію PIC показує значну кореляцію між двома ознаками (P < <0,0001; Рис. 5.5).
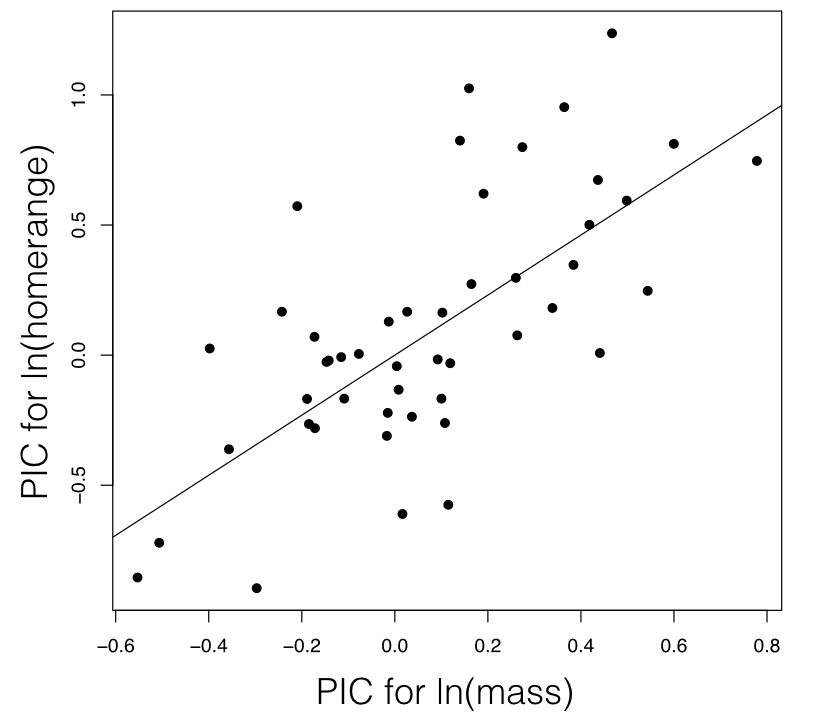
Однак є один недолік регресійного аналізу PIC - не відновлюється оцінка перехоплення регресії y на x - тобто значення y можна очікувати, коли x = 0. Найпростіший спосіб отримати оцінку цього параметра - замість цього використовувати філогенетичні узагальнені найменші квадрати (PGLS). PGLS використовує загальний статистичний механізм узагальнених найменших квадратів і застосовує його до філогенетичних порівняльних даних. У звичайних узагальнених найменших квадратах будується модель співвідношення між y та x, як:
(ур. 5,13)
у = Х Г б +
Тут y - вектор значень ознак n × 1, а b - вектор невідомих коефіцієнтів регресії, які повинні бути оцінені за даними. X D - це матриця дизайну, що включає риси, які потрібно перевірити на кореляцію з y і - якщо модель включає перехоплення - стовпець 1s. Для перевірки на кореляції ми використовуємо:
(ур. 5,14)
XD=[1x11x2……1xn]
У випадку одного предиктора і однієї змінної відповіді, b дорівнює 2 × 1 і отримана модель може бути використана для перевірки кореляцій між двома символами. Однак X D також може бути багатоваріантним і може включати більше одного символу, який може бути пов'язаний з y. Це дозволяє нам проводити еквівалент множинної регресії в філогенетичному контексті. Нарешті, - це залишки - різниця між значеннями y, передбаченими моделлю, та їх фактичними значеннями. У традиційній регресії припускається, що залишки все нормально розподіляються з однаковою дисперсією. На відміну від GLS, можна припустити, що залишки не можуть бути незалежними один від одного; натомість вони є багатоваріантними нормальними з очікуваним середнім нулем та деякою матрицею дисперсії коваріації Ω.
У випадку броунівського руху ми можемо моделювати залишки як мають дисперсії та коваріації, що слідують структурі філогенетичного дерева. Іншими словами, ми можемо замінити нашу філогенетичну дисперсійно-коваріаційну матрицю C як матрицю Ω. Потім ми можемо провести стандартний аналіз GLS для оцінки параметрів моделі:
(ур. 5,15)
ˆb=(X⊺DΩ−1X⊺D)−1X⊺DΩ−1y=(X⊺DC−1X⊺D)−1X⊺DC−1y
Перший член у $\ hat {\ mathbf {b}} $ є філогенетичним середнім $\ bar {z} (0) $. Іншим терміном у $\ hat {\ mathbf {b}} $ буде оцінкою нахилу співвідношення між y та x, обчислення якої статистично контролює ефект філогенетичних зв'язків.
Застосування PGLS до маси тіла ссавців та домашнього діапазону призводить до ідентичної оцінки нахилу та величини P, яку ми отримуємо за допомогою незалежних контрастів. PGLS також повертає оцінку перехоплення цього зв'язку, яку неможливо отримати з PIC.
Звичайно, ще одна відмінність полягає в тому, що PIC та PGLS використовують регресію, тоді як підхід, описаний вище, тестує на кореляцію. Ці два типи статистичних тестів відрізняються. Кореляційні тести для співвідношення між x і y, тоді як регресія намагається знайти найкращий спосіб передбачити y від x. Для кореляції не має значення, яку змінну ми називаємо x, а яку ми називаємо y. Однак в регресії ми отримаємо інший нахил, якщо ми передбачаємо y заданий x замість того, щоб передбачити x заданий y. Модель, яка передбачається моделями філогенетичної регресії, також відрізняється від моделі вище, де ми припустили, що два символи еволюціонують під корельованою броунівською моделлю руху. На відміну від цього, PGLS (і, неявно, PIC) припускають, що відхилення кожного виду від лінії регресії розвиваються під броунівською моделлю руху. Ми можемо уявити, наприклад, що види можуть вільно ковзати вздовж лінії регресії, але що розвивається навколо цієї лінії можна захопити звичайною броунівською моделлю. Інший спосіб подумати про модель PGLS полягає в тому, що ми розглядаємо x як фіксовану властивість видів. Відхилення y від того, що передбачається x, - це те, що розвивається під броунівською моделлю руху. Якщо це здається дивним, це тому, що це так! Існують інші, більш складні моделі моделювання корельованої еволюції двох персонажів, які роблять припущення, які є більш еволюційно реалістичними (наприклад, Хансен 1997); ми повернемося до цієї теми пізніше в книзі. У той же час PGLS є добре використовуваним методом еволюційної регресії і, безсумнівно, корисний, незважаючи на свої дещо дивні припущення.
Аналіз PGLS, як описано вище, передбачає, що ми можемо моделювати структуру похибок нашої лінійної моделі як розвивається під броунівською моделлю руху. Однак можна змінити структуру матриці дисперсії-коваріації помилок, щоб відобразити інші моделі еволюції, такі як Орнштайн-Уленбек. Ми повертаємося до цієї теми в наступному розділі.
