5.2: Що таке еволюційна кореляція?
Іноді серед початківців виникає трохи плутанини щодо того, що саме ми робимо, коли проводимо порівняльний метод, особливо при тестуванні кореляцій символів. Поширена мова, що порівняльні методи «контролю за філогенією» або «видалити філогенію з даних» не обов'язково є просвітницькими або навіть завжди точними. Ще одна поширена припущення полягає в тому, що види не є статистично незалежними і що ми повинні враховувати це порівняльними методами. Хоча точним, я все ще не думаю, що це твердження повністю відображає перспективу деревомислення, що забезпечується порівняльними методами. У цьому розділі я використовую конкретний приклад корельованої еволюції, щоб спробувати проілюструвати силу порівняльних методів та те, чим вони відрізняються від стандартних статистичних підходів, які не використовують філогенії.
У статистиці дві змінні можуть співвідноситися одна з одною. Ми могли б називати це стандартною кореляцією. Коли дві риси співвідносяться, це означає, що враховуючи значення однієї ознаки - скажімо, розмір тіла у ссавців - можна передбачити значення іншого - як площа домашнього ареалу. Кореляції можуть бути додатними (великі значення x пов'язані з великими значеннями y) або від'ємними (великі значення x пов'язані з малими значеннями y). Дивно широке розмаїття гіпотез в біології можна перевірити, оцінюючи кореляції між персонажами.
У порівняльній біології нас часто цікавлять більш конкретно еволюційні кореляції. Еволюційні кореляції виникають, коли дві риси мають тенденцію розвиватися разом через такі процеси, як мутація, генетичний дрейф або природний відбір. Якщо існує еволюційна кореляція між двома персонажами, це означає, що ми можемо передбачити величину і напрямок змін в одному персонажі, враховуючи знання про еволюційні зміни в іншому. Так само, як і стандартні кореляції, еволюційні кореляції можуть бути позитивними (збільшення ознаки x пов'язані зі збільшенням у) або негативними (зменшення x пов'язані зі збільшенням у).
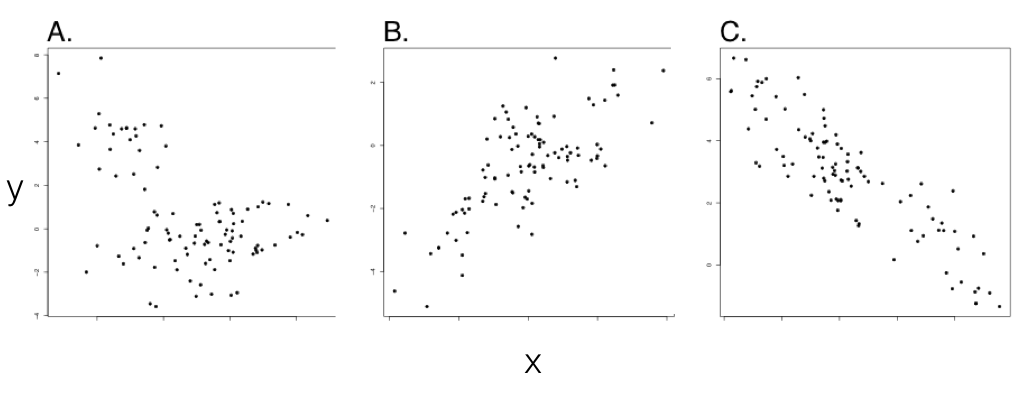
Тепер ми можемо протиставити стандартні кореляції, перевіряючи зв'язки між значеннями ознак у наборі видів, з еволюційними кореляціями - де еволюційні зміни двох ознак пов'язані один з одним. Це ключова відмінність, оскільки лише філогенетична спорідненість може призвести до взаємозв'язку між двома змінними, які насправді не розвиваються разом (рис. 5.1; також див. Felsenstein 1985). У таких випадках стандартні кореляції, правильно, скажуть нам, що можна передбачити значення ознаки y, знаючи значення ознаки x, принаймні серед існуючих видів; але ми були б введені в оману, якби спробували зробити будь-який еволюційний причинний висновок з цієї моделі. У прикладі малюнка 5.1 ми можемо передбачити лише x від y, оскільки значення ознаки x говорить нам, до якої клади належить вид, що, в свою чергу, дозволяє розумно передбачити y. Насправді це класичний приклад випадку, коли кореляція не є причинною причиною: дві змінні співвідносяться лише один з одним, оскільки обидві пов'язані з філогенією.
Якщо ми хочемо перевірити гіпотези про еволюцію ознак, ми повинні спеціально перевірити еволюційні кореляції 1. Наприклад, якщо ми знайдемо зв'язок між незалежними контрастами для двох символів, то ми можемо зробити висновок, що зміни в кожному персонажі пов'язані зі змінами в іншому - висновку, який набагато ближче до більшості біологічних гіпотез про те, чому символи можуть бути пов'язані. У цьому випадку ми можемо думати про статистичні порівняльні методи як орієнтовані на розплутування закономірностей через філогенетичну пов'язаність із закономірностями через ознаки, що розвиваються корельованим чином.