Skip to main content
LibreTexts - Ukrayinska

9.4: Імовірність та аналіз Chi-квадрата

  1. Last updated
  2. Save as PDF
  • Page ID
    6519

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Спостереження Менделя

    чисел

    Ймовірність: Минулі площі Паннетта

    Punnett Squares зручні для прогнозування результату моногібридних або дигібридних схрещувань. Очікування двох гетерозиготних батьків становить 3:1 в одному хресті ознак або 9:3:3:1 у двочерговому хресті. Виконання три-чотири риси хрест стає дуже безладним. У цих випадках краще дотримуватися правил ймовірності. Імовірність - це шанс того, що подія відбудеться, виражена у вигляді частки або відсотка. У випадку моногібридного кросу співвідношення 3:1 означає, що існує\(\frac{3}{4}\) (0,75) шанс домінантного фенотипу з\(\frac{1}{4}\) (0,25) шансом рецесивного фенотипу.

    Одиночна матриця має шанс 1 на 6 бути певним значенням. В цьому випадку є\(\frac{1}{6}\) ймовірність прокатки 3. Зрозуміло, що прокатка другої матриці одночасно не піддається впливу першого і тому є незалежним. Цей другий померти також має\(\frac{1}{6}\) шанс бути 3.

    Ми можемо зрозуміти ці правила ймовірності, застосувавши їх до дигібридного хреста і розуміючи, що ми приходимо до того ж результату, що і моногібридні квадрати Punnett 2, як і з єдиним дигібридним Punnett Square.

    Цей роздвоєний метод обчислення ймовірності потомства з різними генотипами і фенотипами може бути масштабований і застосований до більшої кількості характеристик.

    Тест «Чі-квадрат»

    Статистика σ 2 використовується в генетиці, щоб проілюструвати, чи є відхилення від очікуваних результатів алелів у популяції. Загальне припущення будь-якого статистичного тесту полягає в тому, що між виміряними результатами і прогнозованими відсутні суттєві відхилення. Цей недолік відхилення називається нульовою гіпотезою (H 0). Статистика X 2 використовує таблицю розподілу для порівняння результатів з різними рівнями ймовірностей або критичних значень. Якщо значення X 2 більше значення з певною ймовірністю, то нульова гіпотеза відхилена і спостерігалося значне відхилення від прогнозованих значень. Використовуючи закони Менделя, ми можемо рахувати фенотипи після хреста, щоб порівняти з тими, що передбачені ймовірностями (або площею Пуннетта).

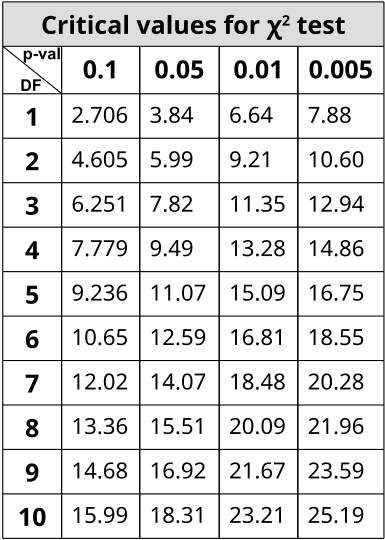
    Для того щоб скористатися таблицею, потрібно визначити терпкість тесту. Чим нижче p-значення, тим жорсткіша статистика. Ступені свободи (DF) також обчислюються, щоб визначити, яке значення на таблиці використовувати. Ступінь Свободи - це кількість класів або категорій, які є в спостереженнях мінус 1. ДФ = N-1

    У прикладі кольору і текстури кукурудзяного ядра є 4 класи: фіолетовий і гладкий, фіолетовий і зморшкуватий, жовтий і гладкий, жовтий і зморшкуватий. Отже, DF = 4 - 1 = 3 і вибираючи p < 0,05 як поріг значущості (відмова від нульової гіпотези), X 2 повинен бути більше 7,82, щоб значно відхилятися від очікуваного. У цьому дигібридному перехресному прикладі ми очікуємо співвідношення 9:3: 1 у фенотипах, де 1/16 населення є рецесивними як для текстури, так і для кольору, тоді\(\frac{9}{16}\) як популяції відображають як колір, так і текстуру як домінанту. \(\frac{3}{16}\)буде домінуючим для одного фенотипу, тоді як рецесивним для іншого, а решта\(\frac{3}{16}\) буде протилежною комбінацією.

    Маючи це на увазі, ми можемо прогнозувати або мати очікувані результати, використовуючи ці співвідношення. Беручи загальний підрахунок 200 подій у населенні, 9/16 (200) = 112,5 тощо. Формально значення σ 2 генерується шляхом підсумовування всіх комбінацій:

    \[\frac{(Observed-Expected)^2}{Expected}\]

    Тест Chi-Square: це монета справедлива чи зважена? (Діяльність)

    1. Кожен в класі повинен перевернути монету 2x і записати результат (припускає, що клас дорівнює 24).
    2. Очікується, що справедливі монети приземлять 50% голів і 50% хвостів.
      • 50% з 48 результатів має бути 24.
      • 24 голови і 24 хвоста вже написані в графі «Очікувані».
    3. Як клас, складіть результати в стовпці «Спостерігається» (всього 48 сальто монет).
    4. В останньому стовпці відніміть очікувані головки від спостережуваних голів і складіть її в квадрат, потім діліть на кількість очікуваних голів.
    5. В останньому стовпчику відніміть очікувані хвости від спостережуваних хвостів і квадратируйте його, потім розділіть на кількість очікуваних хвостів.
    6. Додайте значення з останнього стовпця, щоб створити значення X 2.
    7. Порівняйте значення зі значенням 0,05 з DF = 1.
      • Існує 2 класи або категорії (голова або хвіст), тому DF = 2 — 1 = 1.
      • Чи були монетні сальто справедливими (не суттєво відхиляючись від 50:50)?

    чи квадратна монета

    Припустимо, що підкидання монети дало 26 голів і 22 хвоста. Чи можемо ми припустити, що монета була несправедливою? Якщо ми кидаємо монету непарну кількість разів (наприклад, 51), то ми очікуємо, що результати дадуть 25,5 (50%) голів і 25,5 (50%) хвостів. Але це не можливість. Це коли тест X 2 важливий, оскільки він визначає, чи є 26:25 або 30:21 тощо, ймовірність справедливої монети.

    Хі-квадратний тест забарвлення і текстури ядра в популяції F 2 (активність)

    1. З підрахунків можна припустити, які фенотипи домінантні і рецесивні.
    2. Заповніть категорію «Спостерігається» відповідними підрахунками.
    3. Заповніть «Очікуваний коефіцієнт» з 9/16, 3/16 або 1/16.
    4. Загальна кількість підрахованих подій становила 200, тому помножте «Очікуваний коефіцієнт» x 200, щоб створити поля «Очікуване число».
    5. Обчисліть\(\frac{(Observed-Expected)^2}{Expected}\) для кожної комбінації фенотипів
    6. Додайте всі\(\frac{(Observed-Expected)^2}{Expected}\) значення разом, щоб згенерувати значення X 2 і порівняти зі значенням у таблиці, де DF = 3.
    7. Чи відкидаємо ми нульову гіпотезу чи були спостережувані цифри, як ми очікували приблизно 9:3: 1?
      • Що б це означало, якби нульова гіпотеза була відхилена? Чи можете ви пояснити випадок, коли ми спостерігали значення, які значно змінені від очікуваного?