4: Нове рівняння тиску пари
- Page ID
- 29418
Дистиляція науки (суміш хімії та хімічної інженерії)
Це частина IV, Нове рівняння тиску пари з десяти частин серії технічних статей з дистиляції науки, як в даний час практикується на промисловому рівні. Див. Частина I, Огляд для вступних коментарів, обсягу серії статей та номенклатури. Частини II та III є передумовою до частини IV.
Попередня частина II, Тиск пари стосується рівнянь чистих компонентів, які зазвичай зустрічаються в підручниках, але які мають обмеження в промисловому застосуванні. Частина III, Критичні властивості та ацентричний фактор розробляє ті параметри, які використовуються для взаємозв'язку умовних одиниць температури, тиску та об'єму з їх зменшеними еквівалентами властивостей, а також ацентричний коефіцієнт Пфайзера, який використовується в сучасних рівняннях стану.
Кілька термодинамічно узгоджених форм рівнянь тиску пари (ВП) були розроблені в минулому спеціально для органічних рідин, і, як правило, передбачається, що вони не працюють ні з полярними, ні з сильно пов'язаними з воднем рідинами. Будучи як трохи полярними в природі, так і пов'язаними з воднем, хлоросилани та їх домішки потрапляють саме в це виключення, і тому роблять хороші приклади, що продовжують.
У цій статті температура і тиск використовуються в їх зниженому вигляді, оскільки це дозволяє краще взаємопорівняння між рідинами, є безрозмірним і дозволяє більш глобальний майбутній розвиток. Наведену форму отримують простим діленням звичайної температури, T, на критичну температуру рідини => T r = T/T c. Аналогічно знижений тиск - це звичайний тиск, розділений на критичний тиск рідини => P r = P/P c. Температура і тиск повинні бути в абсолютних одиницях (наприклад, ºK не ºC)
Повертаючись до частини II, E quation 2-4, рівняння Клаузіуса-Клапейрона наведено у скороченому форматі, використовуючи\(\psi \nonumber\) як позначення для термодинамічної похідної природного журналу (відновленого) тиску пари відносно зворотної (зниженої) абсолютної температури:
\[\psi = \frac{-d(\ln P_{r})}{d(1/T_{r})} = \frac{\Delta H_{v}}{\Delta ZRT_{c}} \label{4-1} \]
Для того, щоб мати вдосконалену форму рівняння ВП, яка може бути використана для широкого діапазону між T b і T c (тобто від атмосферного тиску до критичної точки), це співвідношення повинно відповідати наступним критеріям:
- Форма рівняння повинна точно мати зменшене значення VP 1/P c при T b/T c (тобто дає відому температуру кипіння атмосфери при атмосферному тиску), що є добре виміряним лабораторним значенням і легко оцінюється на основі структурних міркувань (див. Частина III Стаття).
- Форма рівняння повинна точно мати зменшене значення ВП одиниці при критичній температурі (тобто відповідати виміряному значенню критичної точки), де зникає рідкий меніск. Це властивість також можна легко оцінити, виходячи зі структурних міркувань (див. Частина III стаття).
- Дайте обґрунтоване значення для зниженого ВП при T r =0,7, відповідне визначенню ацентричного фактора Пфайзера, який має основу в молекулярній складності (див. Частина III стаття).
- Зустрітися з двома термодинамічними тестами консистенції Рейделя, оскільки критична точка наближається (що «α» монотонно падає до найнижчого значення при критичному, і що температурна похідна α = нуль при критичній). Див. крайню ліву частину E quation (\ ref {4-4}) для визначення «α».
Така форма рівняння В.П. дозволила б оцінити сучасні рівняння стану (див. Частина V стаття), міркування про невимушеність (див. Частина VI статтю) та параметри бінарної взаємодії (див. Частина VII стаття). Переважно форма рівняння ВП розумно підходить для більшості рідин (як природних, так і синтетичних), включаючи полярні сполуки та ті, що мають значну водневу зв'язок. Зверніть увагу, що рівняння VP, наведені в частині II, працюють лише у вузьких діапазонах; однак наведені вище критерії #1 та #2 вимагають, щоб форма рівняння VP охоплювала дуже широкий діапазон. У тексті «Властивості газів і рідин», Prausnitz, et al, обговорюються кілька альтернативних форм рівняння ВП, всі з яких відповідають вищезазначеним чотирьом критеріям.
У своїй докторській дисертації в Сіракузькому університеті в 1965 році під керівництвом Леонарда Стіла Річард Тек запропонував саме таку форму рівняння, щоб заповнити технологічну прогалину. Згодом він був опублікований AICHe в 1966 році. На жаль, обчислювальна потужність в той час була дуже обмеженою, тому форми рівнянь з ітераційними рішеннями не могли бути використані; і Інтернет не існував, щоб забезпечити готовий доступ до глобальних даних, взятих за останні багато десятиліть. Використовуючи сучасну комп'ютерну швидкість обробки та програмування, ці обмеження були вирішені, а константи визначені для всіх хлоросиланів та їх електронних домішок.
Як задано рівнянням (\ ref {4-2}) нижче, вихідне рівняння Тек-Стіля В.П. У диференційній формі має два члени: перший, який керує при нижчих тисках, близьких до атмосферного, і другий, який приймає на себе як критичну точку наближається. Хоча Thek встановлюють змінні «q» і «k» рівні константам, щоб уникнути ітераційних рішень, при сучасному програмуванні вони тепер можуть бути оцінені як справжні змінні. Виведення остаточного модифікованого рівняння Тек-Стіля В.П. доступно за запитом, але не відтворюється в цих статтях заради стислості.
\[\frac{d(\ln P_{r})}{d(1/T_{r})} = \frac{A}{T_{r}^2}[1-B_{1}T_{r}+B_{2}T_{r}^2-B_{3}T_{r}^3+B_{4}T_{r}^4...]+ \frac{c}{T_{r}^2}(T_{r}^n-k) \label{4-2} \]
Кілька констант «B» є результатом біноміального розширення загального співвідношення Ватсона для ΔH v. Після скидання B 4 і більш високих термінів розширення як незначних математично та інтегруючи, отримане рівняння зниженого тиску пари становить:
\[ \ln (P_{r})= A[B_{0}-T_{r}^{-1}-B_{1}\ln T_{r}+B_{2}T_{r}-(1/2)B_{3}T_{r}^2]+c\left[\frac{T_{r}^{n-1}-1}{n-1} +k(T_{r}^{-1}-1)\right] \label{4-3} \]
- \(A=\dfrac{\Delta H_{vb}}{RT_{c}(1-T_{br})^q} \nonumber\)
- \(B_{0}=1-B_{2}+(\frac{1}{2})B_{3} \nonumber\)
- \(B_{1}=q \nonumber\)
- \(B_{2}= \dfrac{q(q-1)}{2!} = \dfrac{q(q-1)}{2} \nonumber\)
- \(B_{3}=\dfrac{q(q-1)(q-2)}{3!} = \dfrac{q(q-1)(q-2)}{6} \nonumber\)
- \(c=\dfrac{\alpha_{c} -A(1-B_{1}+B_{2}-B_{3})}{1-k} \nonumber\)
- \(n=(1-k)+\dfrac{A}{c}(1-B_{2}+2B_{3}) \nonumber\)
Оцінка параметрів рівняння ΔH vb, q, k та α c проводиться ітераційно за допомогою методів у частині X, Стратегії збіжності, на основі даних тиску пари, структури молекули та значення T br (знижена температура кипіння атмосфери, Т б/Т с = Т бр). P r має бути одиницею в критичній точці (T r = 1), що дозволяє оцінити константу інтеграції Рівняння 4-3. Дві важливі термодинамічні похідні функції:
\[\frac{d(\ln P_{r})}{d(\ln T_{r})} = \alpha = A(T_{r}^{-1}-B_{1}+B_{2}T_{r}-B_{3}T_{r}^2)+c(T_{r}^{n-1}-\frac{k}{T_{r}}) \label{4-4} \]
\[\frac{-d(\ln P_{r})}{d(1/T_{r})} = \frac{\Delta H_{v}}{\Delta ZRT_{c}}= \psi = A(1-B_{1}T_{r}+B_{2}T_{r}^2-B_{3}T_{r}^3)+c(T_{r}^n-k) \label{4-5} \]
Константи «A» та «B» рівнянь (\ ref {4-2}), (\ ref {4-3}) та (\ ref {4-4}) збігаються з рівнянням (\ ref {4-5}). Оцінка похідної функції Рейделя «α» у Рівнянні (\ ref {4-4}) використовується для встановлення термодинамічної консистенції та дозволяє оцінити параметр рівняння. Зауважте, що похідна Клапейрона від рівняння (\ ref {4-5}) математично ідентична рівнянню рівняння (\ ref {4-1}).\(\psi \nonumber\) \(\psi \nonumber\)буде використана частина V для встановлення прихованої теплоти ΔH v, а також насиченої пари та щільності рідини рідин при різних умовах моделювання ректифікаційної колони.
Використовуючи результати частини III, Модифіковані константи рівняння Тек-Стіля В.П., наведені нижче в таблиці 4-1, для хлоросиланів та електронних домішок, виявлених у виробництві кремнію високої чистоти. Для стислості значення ацентричного фактора, ω, і критичної похідної Ріделя\(\alpha_{c} \nonumber \), в таблиці не наведені. Їх можна обчислити з інших констант рівняння. У деяких випадках електронна домішка може мати як мономерну, так і димерну форму, але форма відзначається в таблиці. Там, де з'єднання не є стабільним, читач відзначить «отвір» в таблиці (наприклад, AlH 3 і Ga 2 H 6 не стабільні як рідини або пари).
Оскільки рішення модифікованого рівняння Tek-Stiel VP обов'язково є ітераційним, застосування цього відношення VP вимагає використання деяких сучасних обчислювальних інструментів для виконання таких ітераційних обчислень (він же «вкладених циклів»). Залежно від уподобань, це може бути зроблено як макрос у програмі електронних таблиць, як MS Excel, або автономної програми, розробленої в BASIC (або MatLab або Fortran). Як уже згадувалося вище, деякі поради щодо стратегії конвергенції наведені в частині X.
Таблиця 4-1 є досить експансивною, щоб проілюструвати, наскільки загальні нові відносини VP. Організація таблиць в основному здійснюється групою Періодичної таблиці (наприклад, група III, група IV та група V) атома ядра молекули, а потім гомологом від гідриду до хлориду. Метилхлорсилани включені як приклади хорошого застосування до рідин, які утворюють межу між класично органічними та неорганічними. Включені два пентани, які представляють промисловий інтерес як електронні домішки, щоб проілюструвати, що нове рівняння ВП корисно і для органічних рідин.
Хоча летючі рідини групи II, групи VI та групи VII, схоже, також слідують новим відносинам ВП, немає записів, наведених у таблиці 4-1, оскільки ці рідини, як правило, не викликають занепокоєння при виробництві електронних матеріалів. Читачеві пропонується слідувати методам оцінювання та стратагемам, наведеним у цих статтях, для подальшого розвитку використання нових рівнянь ВП.
Таблиця 4-1, константи розчину ВП, за групами та гомологом
|
Рідина |
МВТ |
A |
Б 0 |
Б 1 |
Б 2 |
Б 3 |
c |
п |
к |
|
Група ІІІ (А) |
|||||||||
|
Б 2 Ч 6 |
27.670 |
8.9910 |
1.1494 |
0,37848 |
-0.11762 |
0.063573 |
2.8701 |
4.796 |
0,1197 |
|
Б 2 Н 5 Кл |
62.119 € |
8.1915 |
1.1494 |
0,37867 |
-0.11764 |
0.063578 |
3.4560 |
3.8431 |
0,1073 |
|
BH 2 Cl як мономер |
42.284 |
8.3872 |
1.1495 |
0,37888 |
-0.11766 |
0.063583 |
3.2767 |
4 0925 |
0.0938 |
|
BHCl 2 як мономер |
82.722 |
8.9910 |
1.1495 |
0,37937 |
-0.11772 |
0.063596 |
2.7577 |
4.953 |
0.0636 |
|
BCL 3 |
117.169 |
9.5652 |
1.1496 |
0,37988 |
-0.11779 |
0.063609 |
2.2357 |
6.2975 |
0.0291 |
|
AlCl 3 як мономер |
133.341 |
11 9183 |
1.1512 |
0,39300 |
-0.11928 |
0.063892 |
2.2700 |
7.5185 |
0.0291 |
|
Га 2 Н 4 Сл 2 як димер |
214 383 € |
7.0714 |
1.1506 |
0,38810 |
-0.11874 |
0.063799 |
5.346 |
2.5583 |
0.0938 |
|
Га 2 Н 2 Сл 4 як димер |
283 273 € |
10.8499 |
1.1513 |
0,39333 |
-0.11931 |
0.063898 |
3.3656 |
4.9567 |
0.0636 |
|
Га 2 Сл 6 як димер |
352.162 € |
11.1760 |
1.1520 |
0,39974 |
0,11997 |
0.063996 |
3.8566 |
4.5874 |
0.0291 |
|
Група IV (А) |
|||||||||
|
Ши 4 |
32.117 |
7.4652 |
1.1492 |
0,37673 |
-0.11740 |
0.063525 |
3.6247 |
3.4716 |
0.0914 |
|
Ши 3 Кл |
66.562 |
8.8830 |
1.1494 |
0,37847 |
-0.11761 |
0.063572 |
2.7614 |
4.9286 |
0.0756 |
|
Ш 2 сл 2 |
101.007 |
9.9221 |
1.1497 |
0,38068 |
-0.11788 |
0.063629 |
2.1589 |
6.627 |
0.0598 |
|
Сикл 3 |
135.452 |
9.9796 |
1.1501 |
0,38395 |
-0.11827 |
0.063708 |
2.5687 |
5.7950 |
0.0446 |
|
SiCl 4 |
169.896 |
10.0240 |
1.1504 |
0,38651 |
-0.11856 |
0.063765 |
2.8465 |
5.3590 |
0.0291 |
|
Ш (3 СН 3) |
46.144 |
9.0535 |
1.1494 |
0,37855 |
-0.11762 |
0.063574 |
2.6380 |
5.1963 |
0.0758 |
|
Сі 2 Кл (СН 3) |
80.589 |
10.1402 |
1.1499 |
0,38201 |
-0.11804 |
0.063662 |
2.1796 |
6.7338 |
0.0600 |
|
СиНКЛ 2 (СН 3) |
115.034 |
9.1805 |
1.1503 |
0,38512 |
-0.11840 |
0.063735 |
3.346 |
4.3854 |
0.0446 |
|
SiCl 3 (СН 3) |
149.479 |
10.1187 |
1.1506 |
0,38512 |
-0.11840 |
0.063789 |
2.9357 |
5.2665 |
0.0291 |
|
Ш 2 (СН 32) |
60.169 |
8.2747 |
1.1497 |
0,38077 |
-0.11789 |
0.063631 |
3.454 |
3 9214 |
0.0603 |
|
СиНЧ (СН 32) |
94.615 |
9.1914 |
1.1503 |
0,38509 |
-0.11840 |
0.063734 |
3.3232 |
4.4012 |
0.0447 |
|
SiCl 2 (СН 32) |
129.061 |
10.1007 |
1.1507 |
0,38820 |
-0.11875 |
0.063801 |
3.0279 |
5.1285 |
0.0291 |
|
Гех 4 |
76.642 |
8.1986 |
1.1494 |
0,37858 |
-0.11763 |
0.063575 |
3.3615 |
3,9445 |
0.0914 |
|
Гех 3 Кл |
111.087 |
8.6130 |
1.1496 |
0,37993 |
-0.11779 |
0.063610 |
3.1743 |
4.3025 |
0.0756 |
|
Гех 2 Сл 2 |
145.532 |
8.8966 |
1.1498 |
0,38154 |
-0.11798 |
0.063650 |
3.1184 |
4.4929 |
0.0598 |
|
ГеНКЛ 3 |
179.976 |
9.1230 |
1.1501 |
0,38344 |
-0.11821 |
0.063696 |
3.1490 |
4.5641 |
0.0446 |
|
ГеКл 4 |
214.421 |
9.4041 |
1.1503 |
0,38554 |
-0.11845 |
0.063744 |
3.1654 |
4.6724 |
0.0291 |
|
СНН 4 |
122.742 |
9.0298 |
1.1497 |
0,38087 |
-0.11790 |
0.063634 |
3.0671 |
4.5745 |
0.0914 |
|
SnCl 4 |
260.521 |
10.1994 |
1.1506 |
0,38745 |
-0.11867 |
0.063744 |
2.8471 |
5.4354 |
0.0291 |
|
Група V (A) |
|||||||||
|
РН 3 |
33.998 |
7.8041 |
1.1485 |
0,37228 |
-0.11684 |
0.063396 |
2.8050 |
4.3644 |
0.1009 |
|
РН 2 Кл |
68.443 |
8.6412 |
1.1490 |
0,37518 |
-0.11721 |
0.063482 |
2.4920 |
5.2267 |
0.0766 |
|
ПГКЛ 2 |
102.888 |
8.5412 |
1.1495 |
0,37919 |
-0.11770 |
0.063591 |
3.0719 |
4.3813 |
0.0527 |
|
пКл 3 |
137.333 |
7.2366 |
1.1501 |
0,38413 |
-0.11829 |
0.063712 |
4.4289 |
2.9789 |
0.0291 |
|
ОпКЛ 3 |
153.331 |
9.7746 |
1.1500 |
0,38331 |
-0.11819 |
0.063693 |
2.4586 |
5.9576 |
0 |
Таблиця 4-2, рішення ВП, за групами та гомологом, продовження
|
Рідина |
МВТ |
A |
Б 0 |
Б 1 |
Б 2 |
Б 3 |
c |
п |
к |
|
Група V (A), прод. |
|||||||||
|
АШ 3 |
77.945 |
7.4208 |
1.1484 |
0.37116 |
-0.11670 |
0.063362 |
2.9474 |
4.0298 |
0.1009 |
|
АШ 2 Кл |
112.390 |
8.5242 |
1.1488 |
0,37403 |
-0.11707 |
0.063448 |
2.3972 |
5.3468 |
0.0766 |
|
ЯСЛ 2 |
146.835 |
9.3548 |
1.1493 |
0,37782 |
-0.11754 |
0.063555 |
2.1821 |
6.2831 |
0.0527 |
|
АСЛ 3 |
181.281 |
10.0281 |
1.1499 |
0,38254 |
-0.11810 |
0.063675 |
2.2519 |
6.5171 |
0.0291 |
|
СбН 3 |
124.781 |
8.5409 |
1.1484 |
0,37136 |
-0.11673 |
0.063368 |
2.0491 |
6.0821 |
0.1009 |
|
SBCl 3 |
28.115 |
7.1200 |
1.1511 |
0,39192 |
-0.11916 |
0.063873 |
5.345 |
2.6317 |
0.0291 |
|
н-пентан |
72.149 |
10.0508 |
1.1504 |
0,38593 |
-0.11849 |
0.063753 |
2.6269 |
5.7673 |
0 |
|
ізо-пентан |
72.149 |
9,9797 |
1.1502 |
0,38432 |
-0.11831 |
0.063717 |
2.4514 |
6.0715 |
0 |
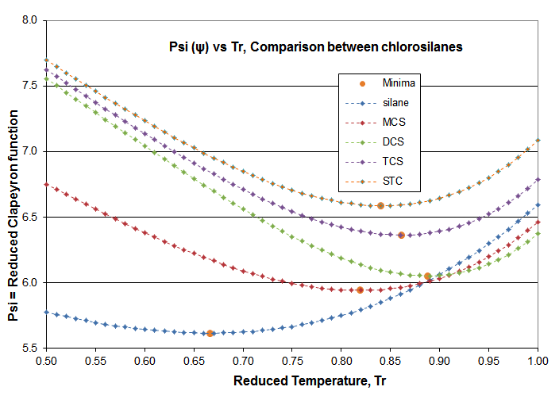
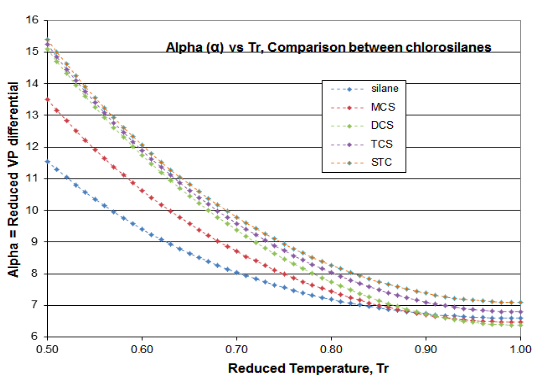
На малюнку 4-3 пропонуються дві ділянки, щоб підтвердити принципи цієї статті про дистиляцію науки. Ці ділянки призначені для функції\(\psi \) (Psi) рівняння (\ ref {4-5}) та\(\alpha \) (альфа) функції рівняння (\ ref {4-4}), для хлоросиланового гомологу. Похідна функція\(\phi \) проходить через необхідний мінімум, який створює очікуваний перегин у кривій тиску пари, як правило, близько T r = 0,80-0,86. Мінімум силану\(\phi \) відбувається при T r = 0,67, а мінімум\(\phi \) DCS - при T r = 0,89. Той факт, що дві рідини цього гомологу є викидами, ілюструє, чому тиск парів хлоросилану настільки погано відповідає вираженням ВП, які призначені для використання з вуглеводнями. Однак можна побачити, як\(\alpha \) функція Рейделя відповідає вимогам термодинамічної консистенції: для всіх рідин гомологу\(\alpha \) функція асимптотизує до постійного значення (\(\alpha_{c} \)) у міру наближення критичної точки, при цьому нахил\(\alpha \) функції збирається до нуля як критичний наближається.
Інша перевірка валідації показана на малюнку 4-4, порівнюючи тиск пари хлоросиланів та хлорофосфінів, які є програмами дистиляції розділення у всіх комерційних очищеннях хлоросилану.
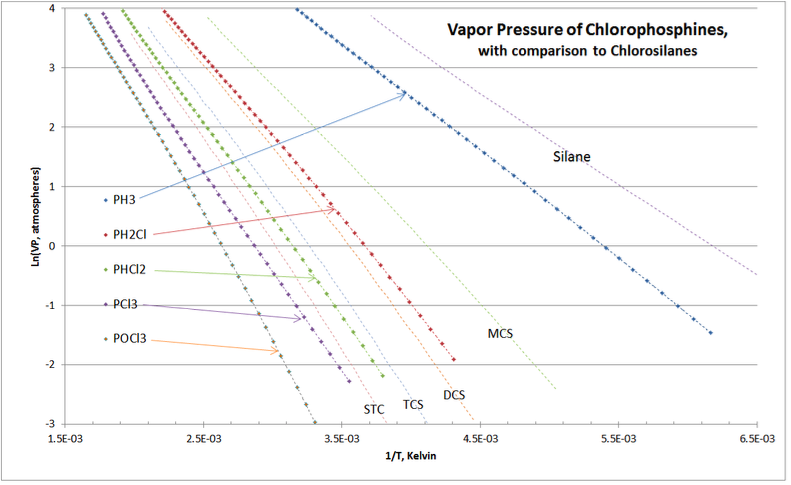
Як і очікувалося, криві VP хлорофосфіну гомолога «гніздяться» навколо хлоросиланів. Перехресних кривих немає, а розташування кривих тиску пари хлорофосфіну лежать саме так, як вони досвідчені в комерційній практиці дистиляційних колон очищення хлоросилану.
Оскільки математика в Equation (\ ref {4-3}) дещо задіяна, наводиться приклад з розрахунками.
Приклад: При тиску 3,50 атмосфер яка температура кипіння трихлорсилану (ТКС)?
З частини III, Таблиця 3-3, відповідні значення властивостей для TCS є: T c = 479,15° K і P c = 41.15 атм. MW, T b, V c і Z c для цього прикладу не потрібні. З частини IV константами розв'язку ВП для ТКС є: A=9.9796; B 0 = 1,1501; B 1 = 0.38395; B 2 = -0.11827; B 3 = 0.063708; c = 2.5687; n = 5.7950; і k = 0,0446.
Як і всі вдосконалені рівняння VP, визначення температури кипіння TCS в 3,50 атмосфер є ітераційним; тому приємно мати графік VP, щоб отримати гарне перше припущення. Використання наведеного вище рисунка 4‑4, для
\ ln (VP) =\ ln (3.50) = 1.2528, схоже, 1/T = 2.89E-3 може бути гарною першою здогадкою => T = 346° K; тому спочатку вгадайте T r = 346/479.15 = 0.7221. Підключення цього першого значення припущення T r до рівняння T-S VP з константами вище:
\( \ln (P_{r})= A[B_{0}-T_{r}^{-1}-B_{1}\ln T_{r}+B_{2}T_{r}-(1/2)B_{3}T_{r}^2]+c[\frac{T_{r}^{n-1}-1}{n-1} +k(T_{r}^{-1}-1)] \nonumber\)дає зменшене значення ВП P r = 0,08273; так VP=0.08273*41.15 = 3,404 атм, що трохи менше бажаного 3,50 атм. Таким чином, T потрібно трохи збільшити від початкового першого припущення 346° K.
Повторне виконання рівняння TCS VP з T = 347° K дає ВП 3,50 атм (примітка: 347.05°K є відповіддю, якщо рішення розроблено до двох знаків після коми температури). Отже, температура кипіння при 3,50 атмосфер становить 347° К або 73,9° C.
