7: Коефіцієнти активності рідини

Дистиляція науки (суміш хімії та хімічної інженерії)

Це частина VII, коефіцієнти активності рідини з десяти частин серії технічних статей з дистиляції науки, як в даний час практикується на промисловому рівні. Див. також Частина I, Огляд вступних коментарів, обсяг серії статей та номенклатури.

Частина VII, Коефіцієнти активності рідини будуються на частині VI, Fugacity щодо відходу паро-рідких рівноваг (VLE) бінарних сумішей від ідеальної поведінки, як це зазвичай зустрічається в практичному застосуванні науки про дистиляцію. У поєднанні з попередніми статтями мета цієї статті полягає в тому, щоб завершити пояснення рівноважної поведінки бінарних систем; таким чином, що частина IX може проілюструвати приклад проектування процесу дистиляції.

У частині VI було введено поєднання Закону Рауля та Закону Дальтона, що регулює ідеальну паро-рідинну поведінку летких рідинних сумішей, з повторенням рівняння 6-1 для зручності.

\( Y_{1}=(X_{1} \times VP_{1})/(X_{1} \times VP_{1} + X_{2} \times VP_{2}) \nonumber\)\( Y_{2}=(X_{2} \times VP_{2})/(X_{1} \times VP_{1} + X_{2} \times VP_{2}) \nonumber\)повторити рівняння 6-1

Також у частині VI реальний відхід від ідеальної поведінки обговорювався стосовно коефіцієнтів нечіткості, але не вистачало коефіцієнтів активності рідини. Рівняння 6-4, повторене нижче, дало повну залежність між парціальним тиском i-го компонента, PP _i, і чистокомпонентним тиском пари ВП _i, для рідких і парових мольних фракцій X _i і Y _i, відповідно. Загальний тиск в системі (сума парціальних тисків) позначається як\(\pi \nonumber\); (\(\phi_{i}^V\nonumber\)&\(\phi_{i}^L\nonumber\)) - коефіцієнти розпускання рідини і пари. \(\gamma_{i} \nonumber\)- коефіцієнт активності рідини i-го компонента для цього конкретного набору компонентів.

\(Y_{i} \times \pi =PP_{i} =(\phi_{i}^L/ \phi_{i}^V) \times \gamma_{i} \times VP_{i} \times X_{i} \nonumber\)повторити рівняння 6-4

Наведено приклад у частині VI випаровуючої суміші TCS-STC, що контрастує рівноваги пари та рідини (VLE), очікувані від Раулта/Далтона; від того, що насправді відбувається в реальному світі внаслідок відходів ідеальності. Підсумовуючи попередню статтю, більш летюча рідина впливає на менш летючу рідину, щоб збільшити її видимий тиск пари; і менш летюча рідина зменшує тиск пари більш летючої рідини. Чистий ефект полягає в тому, щоб ускладнити поділ компонентів за допомогою дистиляції (наприклад, більше теоретичних лотків або збільшеної кількості рефлюксу, ніж очікувалося). Детальне обговорення коефіцієнтів нечіткості див. Частина VI.

Як примітка «домашнє господарство», слід підкреслити, що частини VI та VII розглядають коефіцієнти невимушеності та коефіцієнти активності рідини окремо. У деяких текстах дві теми стискаються разом за допомогою конкретних моделей змішування та рівнянь стану (EOS). Однак два фактори відходу ідеальності по-різному базуються, і їх комбінація часто дає помилкові або нісенітниці результати при використанні з полярними рідинами або тими, які мають високий ступінь водневого зв'язку (наприклад, хлоросилани, які використовуються як постійні приклади). Коефіцієнти невибагливості природно виникають внаслідок відмінностей у летючості рідини. Коефіцієнти активності рідини виникають внаслідок відмінностей у властивостях рідини, включаючи критичну температуру (T _c), критичний тиск (P _c), критичний об'єм (V _c) та ацентричний фактор (ω), а також ефекти ентропії та ентальпії змішування (згадуються в термодинамічних текстах як надлишок вільної енергії Гіббса).

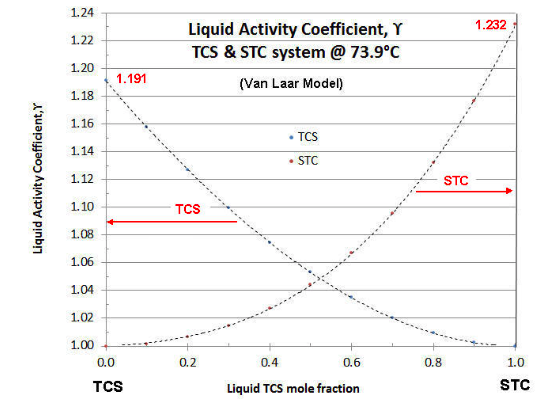
Для заданої температури та комбінації рідин значенням\(\gamma \nonumber\) є функція рідкої мольної фракції, асимптотично піднімаючись від одиниці за умови чистого компонента. Зазвичай значення\(\gamma \nonumber\) для системи будуються як функція мольної частки більш летючого компонента. Приклад такого графіка наведено на малюнку 7-1, для двійкового файлу TCS-STC при 73,9°C (температура продовжуючого прикладу попередніх статей).

Малюнок 7-1, Коефіцієнти активності рідини TCS-STC при 73,9° C

Існує кілька моделей коефіцієнтів активності рідини, які термодинамічно узгоджені (тобто дотримуйтесь правила Гіббса-Дюхема термодинаміки бінарної системи). Двоконстантна модель Ван Лаара найпростіша в маніпулюванні, але обмежена двійковими системами. Модель Маргулеса не тим чим відрізняється від моделі Ван Лаара, а також обмежена двійковими системами. Модель Вільсона є більш складною математично, але може бути застосована до потрійних або більш числових компонентних систем. На щастя параметри моделі Вілсона можна розрахувати за моделлю Ван Лаара. Відомі ще більш складні моделі коефіцієнтів активності рідини (наприклад, NRTL та UNIQUAC), але для ефективної оцінки вони потребують більшої кількості точок даних. У випадку з вищевказаним сюжетом показана модель Ван Лаара. У частині VIII методи обговорюються для оцінки експериментальних даних про коефіцієнти активності рідини та пристосування даних до моделі. У більшості випадків з хлоросиланами (та їх домішками) якість даних не така велика, тому простіший Ван Лаар зазвичай використовується для кореляції даних та оцінки бінарних систем, а модель Вільсона використовується для потрійних систем та за її межами. Для більш глибокого обговорення коефіцієнтів активності рідини читач посилається на текст «Властивості газів і рідин», Рейд, Праусніц і Шервуд, (McGraw-Hill). Третє видання більш читабельне, але п'яте видання більш оновлене.

Модель Ван Лаара:

\[Ln(\gamma_{1}) =A_{1} \times [1+(A_{1} \times X_{1})/(A_{2} \times X_{2})]^{-2} \label{7-1} \]

\(Ln(\gamma_{2}) =A_{2} \times [1+(A_{2} \times X_{2})/(A_{1} \times X_{1})]^{-2} \nonumber\)

при цьому A ₁ і A ₂ є константами Ван Лаара для більш летючої та менш летючої складової відповідно.

Зручно,\[EXP(A_{1}) = \gamma_{1} @ X_{2} \rightarrow 0 \label{7-2} \]

\(EXP(A_{2}) = \gamma_{2} @ X_{1} \rightarrow 0 \nonumber\)

що спрощує оцінку. Зверніть увагу на рисунок 7-1, що графік коефіцієнтів активності рідини не завжди симетричний (тобто A ₁ ≠ A ₂). На графіку рисунка 7-1, A ₁ (TCS) = 0,1752, тому крива ТКС асимптотизується при\(\gamma \nonumber\) = 1.191; а A ₂ (STC) = 0,2086, тому крива ТКС асимптотизується при\(\gamma \nonumber\) = 1.232.

Завершуючи поточний приклад з частини VI, для рідкої суміші TCS-STC, з 40% молярним TCS, при 73,9° C, для визначення мольної фракції пари в рівновазі (але тепер включаючи ефекти коефіцієнта активності рідини):

У частині VI тиск парів чистих компонентів TCS та STC відповідно обчислювали з рівняння ВП частини IV відповідно 3,500 та 1,651 атмосфер при 73,9° C, а також з частини V розраховували рідкі та парові слабкості відповідно Таблиця 6-1, повторена нижче, з використанням Peng-Robinson EOS (частина V).

Повторіть таблицю 6-1: Порівняння коефіцієнтів нечіткості TCS та STC

	TCS	СТК
\(\phi^L \nonumber\)	0.9976	1,0039
\(\phi^V \nonumber\)	1.0488	0,9562
\(\phi^L / \phi^V \nonumber\)	0,9512	1.0498

Значення для\(\gamma \nonumber\) обчислюються для TCS і STC @ 0,40 мф TCS, за E quation (\ ref {7-1}), використовуючи значення для A ₁ і A ₂ вище (або просто читати з рис. 7-1), щоб бути 1.075 і 1.027 відповідно. Підключивши всі ці значення до рівняння 6-4 (повторюється вище), парціальні тиски TCS та STC при 73,9° C:

\(PP_{TCS} =0.9512 \times 1.075 \times 3.500 \times 0.40 =1.432 \nonumber\)атмосфери, і

\(PP_{STC} =1.0498 \times 1.027 \times 1.651 \times 0.60 =1.068 \nonumber\)атмосфер.

Отже\(Y_{TCS} = 1.432/(1.432+1.068) =.573 \nonumber\), значення, яке було дано в частині VI, при цьому моль частка STC дорівнює 0,427.

Уважний читач побачить, що не тільки парціальні тиски TCS і STC відрізняються від Raoult/Dalton, але і загальний тиск. В ідеальній поведінці Раульта/Дальтона парціальні тиску були наведені в частині VI як 1.400 і 0.991 атмосфер, для загального тиску 2,39 атмосфер. Але насправді при 73,9° C і 0,40 мф TCS загальний тиск натомість становив би 2,50 атмосфер. Таким чином, хоча відхилення ідеальності TCS зробили частку парової молі меншою (0.573 проти 0.586), і TCS, і STC чинили трохи більше парціального тиску, ніж вказував би Раульт. Але кротова фракція ТКС все ж пішла вниз, тому що ідеальність відходу STC була більшою, ніж у TCS.

Винос з цього прикладу полягає в тому, що, хоча Раульт/Далтон дасть вам «швидке та брудне» значення для Y/X, легко отримати загальну неправильну відповідь для визначення вимог конструкції ректифікаційної колони. Майже в кожному випадку промислової практики використання Raoult/Dalton зменшить кількість лотків, необхідних для поділу (або для тієї ж кількості лотків, зменшити необхідний флюкс). З цієї причини важливо знати, як розробити кращу відповідь.

Для багатьох двійкових систем дані VLE існують - але, як правило, не при температурі/тиску, необхідному для промислового дизайну. Більшість промислових зразків використовують більш високі тиску для економії габаритів, а також для розміщення наявних джерел енергії для приводу колони ребойлера і конденсатора. Проте практичність збору даних в лабораторії зазвичай вимагає тиску трохи вище навколишнього середовища або при невеликому вакуумі. Особливо це стосується хлоросиланів, оскільки звичайні матеріали конструкції для більш високого тиску можуть каталізувати повільні побічні реакції, такі як диспропорція та димеризація.

Лабораторні дані зазвичай збираються на основі невеликих кількостей рідини, які використовуються неодноразово при дещо різних комбінаціях температури та складу. У випадку з електронними домішками деякі з цих сполук не дуже стабільні поза хлоросиланової матриці. Тому необхідно використовувати кореляційний метод, який дозволяє певну ступінь екстраполяції.

У 1981 Chung-Ton Lin і Thomas Daubert з Університету штату Пенн розробили таку модель коефіцієнта активності рідини і опублікували те ж саме в промислової та інженерної хімії проектування та розробки процесів, базуючи свою роботу на неполярних вуглеводневих сумішах. Я використовував їх загальний метод, але модифікував дві константи так, щоб краще відповідати наявним VLE даних про хлоросилани. Використовуючи ці переоцінені константи, переглянутий метод «Lin & Daubert» (детально описаний нижче як E quation (\ ref {7-3}) був використаний для перевірки промислово отриманих даних про дистиляційне очищення TCS і силану, з хорошими результатами. Очевидно, що більше даних було б краще, особливо про потрійні суміші та електронні домішки низької концентрації в хлоросиланах. Однак, поки таке не стане доступним, рекомендується E quation (\ ref {7-3}) нижче.

Щоб розробити загальний вираз для параметрів Ван Лаара (\(A_{i} \nonumber\)&\(A_{j} \nonumber\)), Lin & Daubert повертаються до оригінального двочленного виразу Ван Лаара щодо надлишкової енергії Гіббса змішування, використовуючи Рівняння стану SRK для часткової молярної стисливості та простих правил змішування; і розширити його в наступне:

\[A_{i} = c \times F_{i} +d \times k_{ij} \times G_{i} \label{7-3} \]

\(A_{j} = c \times F_{j} +d \times k_{ij} \times G_{j} \nonumber\)

• \(F_{i} =1/[T_{ri}P_{ci}] \times (R_{i} \times (1+M_{j})^{0.5} \times P_{ci}^{0.5} - R_{j} \times (1+M_{j})^{0.5} \times P_{cj}^{0.5})^2 \nonumber\)
• \(F_{j} =1/[T_{rj}P_{cj}] \times (R_{j} \times (1+M_{i})^{0.5} \times P_{cj}^{0.5} - R_{i} \times (1+M_{i})^{0.5} \times P_{ci}^{0.5})^2 \nonumber\)
• \(G_{i} = T_{ri}^{-1} (P_{cj}/P_{ci})^{0.5} \times R_{i} \times (1+M_{i})^{0.5} \times R_{j} (1+M_{i})^{0.5} \nonumber\)
• \(G_{j} = T_{rj}^{-1} (P_{ci}/P_{cj})^{0.5} \times R_{j} \times (1+M_{j})^{0.5} \times R_{i} (1+M_{j})^{0.5} \nonumber\)
• \(M_{i} = 0.480 + 1.574\omega_{i} -.176\omega_{i}^2 \nonumber\)\(M_{j} = 0.480 + 1.574\omega_{j} -.176\omega_{j}^2 \nonumber\)
• \(R_{i} =[1+M_{i} \times (1-T_{ri}^{0/5})]^{0.5} \nonumber\)\(R_{j} =[1+M_{j} \times (1-T_{rj}^{0/5})]^{0.5} \nonumber\)
• \(k_{ij} =1 - 2 \times [V_{ci}^{1/3} \times V_{cj}^{1/3}]^{0.5} / [V_{ci}^{1/3} + V_{cj}^{1/3}] \nonumber \)

Використовуючи вдосконалений набір curve-fits для «c»,

• \(0< \Delta \omega <0.03 ⇒ \nonumber\)\( Ln(c)= -8.0637E+04(\Delta \omega)^3 +8.2649E+03(\Delta \omega)^ 2 - 3.2891E+02 (\Delta \omega) +5.5051 \nonumber\)
• \(0.03 < \Delta \omega <0.30 ⇒ \nonumber\)\( Ln(c)=6.4645E+02(\Delta \omega)^4 -7.9857E+02(\Delta \omega)^3 +3.4768E+02(\Delta \omega)^2 -6.5099E+01(\Delta \omega) +2.5667 \nonumber\)

Зменшуючи наявні дані VLE до параметрів Ван Лаара та коригуючи коефіцієнти неміцності пари та рідини, найкраще значення «d» встановлено 112.1 для хлоросиланів та подібних рідин.

Lin & Daubert запропонували обмежувати функцію «c» на основі їхніх даних; але використання вищезгаданого вдосконаленого набору поліномів для «c» дозволяє уникнути особливостей під час ітераційних обчислень, з мінімальним «c» 0,135 (як «Δω» → ∞)\(0.005 < \Delta \omega=|\omega_{i} - \omega_{j}| <0.15 \nonumber\)

Зверніть увагу, що змінна «c» у першому семестрі Рівняння 7-3 базується на\(F_{i} \nonumber\) значеннях та відмінностях між ацентричним фактором двох рідин, ω (тобто їх молекулярна складність); тоді як другий член рівняння 7-3 базується на\(G_{i} \nonumber\) значеннях та відмінностях між двома рідинами молекулярні обсяги при критичних (V _c).

---

Повертаючись до попереднього прикладу TCS-STC та використовуючи критичну температуру двох компонентів (T _c), критичний тиск (P _c), критичний об'єм (V _c) та ацентричний коефіцієнт (ω), а також базуючи знижену температуру (T _r) на 73,9° C = 347,05° C, E quation (\ ref {7-3}) дає значення A ₁ і A ₂, використані раніше в цій статті, 0,1752 і 0,2086 відповідно.

Часто оцінюючи різні конструкції дистиляції для процесу, дизайнер стикається з необхідністю зміни температури процесу та визначення впливу на Y/X за допомогою рівняння 6-4, повтореного вище. Це не викликає проблем при оцінці коефіцієнта невимушеності\(\phi_{i}^L / \phi_{i}^V \nonumber\), оскільки ці фактори походять від EOS (див. Частина VI). Однак, якщо за допомогою експериментально отриманих значень для\(\gamma \nonumber\) того, щоб були отримані при іншій температурі, потрібна подальша коригування. Загальне «правило великого пальця», яке спостерігається в деяких текстах, полягає в тому, що Ln (\(\gamma \nonumber\)) пропорційний 1/T (абсолютна температура) для невеликих змін температури. Насправді таке «правило великого пальця» рівносильно припущенню, що змішувальні ефекти багатокомпонентної рідини ближче до ізотермічної моделі, ніж ізентальпічна. У більшості випадків температурна залежність від коефіцієнта активності являє собою суміш двох теоретичних моделей, що призводить до співвідношення:

\[Ln(\gamma_{i})=a + \frac{b}{T} \label{7-4} \]

де «a» і «b» - константи лінійної залежності («a» = 0, що ведуть до ізентальпічної моделі, або «b» = 0, що ведуть до ізотермічної моделі). Використання E quation (\ ref {7-3}) вирішує проблему, оскільки вона прогнозує такі зміни температури по лініях E quation (\ ref {7-4}), і тому може використовуватися відносним чином. Наприклад, якщо встановлено, що E quation (\ ref {7-3}) перепрогнозує значення\(Ln(\gamma) \nonumber\) на 10% від експериментально отриманого значення коефіцієнта активності, то обчислити, скільки E quation (\ ref {7-3}) буде передбачати різну температуру, і застосувати, що 10% на\(Ln(\gamma) \nonumber\).

Зверніть увагу, що за всіма намірами коефіцієнт активності рідини не є прямою функцією тиску, крім збільшення температури кипіння збільшує тиск. Однак fugacities є функцією як температури, так і тиску, і саме тому їх слід включати в розрахунки Y/X (багато текстів виступають за встановлення fugacity до єдності, що лише близько до того, щоб бути дійсним при дуже низькому тиску).

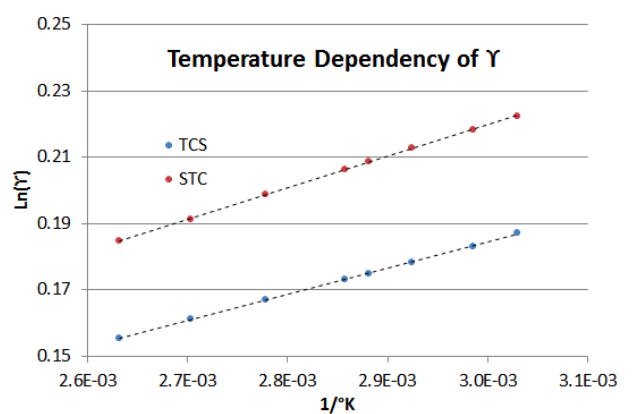
Щоб продемонструвати, як Equation (\ ref {7-3}) працює зі змінною температурою (від 330° K до 380° K), на малюнку 7-2 показано залежність для асимптотичних BIP суміші TCS-STC у наведеному вище прикладі. Зверніть увагу, що нахил лінії коефіцієнта активності рідини STC приблизно на 20% крутіший, ніж у лінії коефіцієнта активності рідини TCS (тобто в бінарній системі TCS-STC підвищення температури має більший вплив на STC,\(\gamma \nonumber\) ніж на TCS\(\gamma \nonumber\)).

Рисунок 7-2, Температурна залежність Ln () при асимптотах