8: Методи аналізу VLE

Дистиляція науки (суміш хімії та хімічної інженерії)

Це частина VIII, Методи аналізу VLE з десяти частин серії технічних статей з дистиляції науки, як в даний час практикується на промисловому рівні. Див. також Частина I, Огляд вступних коментарів, обсяг серії статей та номенклатури.

Частина VIII, Методи аналізу VLE рекомендує методологію, яка використовується при зборі даних коефіцієнтів активності рідини бінарних систем (див. Частина VII). Ця стаття також стосується перевірки, особливо коли збір даних здійснюється на реактивних рідин, таких як хлоросилани, які можуть непропорційно або димеризуватися під час дослідження.

У цій статті використовується інформація частин III-VII.

У частині VII наведено кореляційну методику оцінки коефіцієнтів активності рідини. Як згадувалося в попередній статті, зазвичай збирають дані про такі рівноваги пари та рідини (VLE) в лабораторії, в умовах, близьких до тиску навколишнього середовища. Тим не менш, багатьом промисловим застосуванням часто потрібно використовувати результати VLE при більш високих технологічних тиску/температурах або різних складах. Щоб уникнути плутанини позначень між коефіцієнтом активності рідини (\(\gamma_{i} \nonumber\)) та мольної фракцією пари (Y _i), мольні фракції X і Y показані жирним шрифтом.

Нагадаємо, з частин VI і VII, що коефіцієнти невибагливості (\(\phi_{i}^V\nonumber\)&\(\phi_{i}^L\nonumber\)) - це функції температури і тиску. Однак коефіцієнт активності рідини s (\(\gamma_{i} \nonumber\)) є функціями лише температури та мольної частки. В експериментальній ситуації розрахункові значення\(\gamma_{i} \nonumber\) (від значень Y _{i і X i} = парофазна моль фракція і рідкофазна моль фракція) найлегше співвіднести, коли температура в системі тримається постійною, а тиск в системі допускається варіюватися. Зазначено інакше, дані P XY @ константа T набагато легше збирати та співвідносити, ніж T XY @ константа P. Однак у комерційних додатках ректифікаційна колона, як правило, контролюється при постійному тиску. Отже, поширеною помилкою промислового зв'язку є запит лабораторії для збору даних VLE як T XY @P, але замість цього отримати P XY @T. Існує спосіб перетворити один набір даних в інший зв'язок, але це дещо незручно і вимагає вибору моделі коефіцієнта активності.

На малюнку 7-1 частини VII показаний очікуваний профіль\(\gamma \nonumber\) проти X @ постійної T, а на малюнку 7-2 частини VII показаний очікуваний профіль\(\gamma \nonumber\) проти T @ постійної X, на осях X = 0 та X = 1. Причиною створення коефіцієнтів активності рідини експериментально, як правило, є використання лабораторних результатів для проектування ректифікаційної колони, з упевненістю, що\(\gamma \nonumber\) може бути точно відомо при будь-якому значенні X або T, щоб встановити співвідношення Y/X вгору і вниз по конструкції колони. Використовуючи принципи частин VI і VII, ці проблеми можуть бути вирішені.

Встановивши експериментальний протокол, необхідно розглянути вплив обладнання для збору даних на аналізувані рідини та перевірити якість рідин для зразків. Для реактивних рідин, таких як хлоросилани, це означає, що використання скляного посуду, здатного до тиску, є найкращим вибором (або нікельованої сталі як другий вибір), оскільки деякі легуючі елементи нержавіючої сталі повільно каталізують реакції диспропорції, які змінюють склади зразків.

Також важливо перевірити чистоту зразків рідини, на відміну від сліпого прийняття аналізу будь-якої супутньої інформації постачальника. Знову ж таки, з хлоросиланами (як це характерно для реактивних рідин), транспортний контейнер може каталізувати побічні реакції (тобто COA постачальника, можливо, був точним, коли зразок завантажувався в контейнер, але чистота погіршилася під час відвантаження). Зазвичай 99,99% чистих зразків TCS (під інерцією аргону) від авторитетних постачальників в кінцевому підсумку мають кілька відсотків DCS та кілька відсотків STC, а також кілька десятих відсотків гексахлордисилану та кілька десятих відсотків водневого газу, коли вони використовуються лише через кілька тижнів. Хорошою практикою перед завантаженням рідин для зразків у лабораторне обладнання є подвійна перегонка зразків (відкидання фракцій «вогнів» та «важких» та запевнивши, що використовується лише фракція «серцевого розрізу»: тиск кипіння якої ідентичний очікуваному тиску пари чистого компонента).

При зазначених вище запобіжних заходах дані збираються в 15-20 (або більше) точках X, Y, з деякими дублікатами пізніше під час запуску для встановлення точності експериментального аналізу та підтвердження відсутності системної помилки (наприклад, забруднення). Принаймні дві пари точок даних повинні бути зібрані близько до X = нуля і X = одиниці. Щоб підтвердити температурну залежність коефіцієнтів активності, слід зібрати принаймні три набори даних (кожен при різній постійній температурі або тиску).

Після збору даних лабораторна робота призупиняється, але тоді для підтвердження достовірності даних перед тим, як звітувати або використовувати результати, необхідні «числові хрусткі». Якщо достовірність даних не підтверджена, помилка повинна бути знайдена і лабораторні роботи повторити. Спочатку складіть набір даних і перевірте, чи крива P- X і крива P- Y, або крива T- X і крива T- Y показують однакове перетин як на нульових, так і на одиничних мольних осей дробу; і що перетину осей точно репрезентативні кожному чисто- відомий тиск пари компонента. Якщо криві X і Y не перетинаються при правильному значенні на кожній осі, є деякі систематичні помилки в наборі даних, які повинні бути вирішені, перш ніж буде виконана будь-яка більш оціночна робота. Пошкоджений набір даних, швидше за все, буде мати лише мінімальне значення при встановленні коефіцієнтів активності; і частіше є причиною викинути все це і повторно виконати роботу після того, як системна помилка буде вирішена.

Використовуючи алгебраїчну модифікацію попереднього рівняння 6-4, коефіцієнти активності, обчислюються\(\gamma_{i} \nonumber\) _i для кожної точки даних P- X та P- Y.

\[\gamma_{i} =(\phi_{i}^V/\phi_{i}^L) \times (Y_{i} \times \pi)/(VP_{i} \times X_{i}) \label{8-1} \]

де\(\pi \nonumber\) - загальний тиск,\(VP_{i} \nonumber\) - тиск пари i-го компонента і\((\phi_{i}^V/\phi_{i}^L) \nonumber\) співвідношення пар/рідини цього компонента.

Малюнок 8-1, T XY/P дані VLE на системі TCS-STC

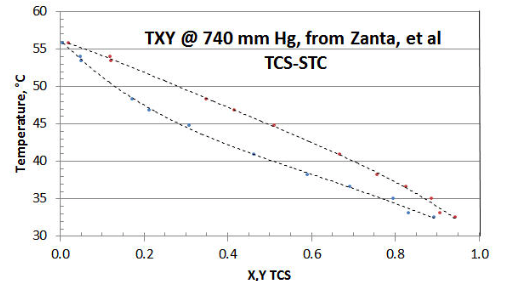
На малюнку 8-1 показано дванадцятиточковий T XY/P набір даних Zanta et al від Chemicky Prumysl (Чеська хімічна промисловість), використовуючи графік електронних таблиць. Дослідники зібрали кілька точок даних поблизу осі STC (тобто TCS = нуль). Однак було б краще мати кілька більше зібраних близько до іншої (тобто TCS = єдності) осі; і щоб всі дані повідомляли з більшою точністю. Дослідники вирішили збирати дані при постійному тиску 740 мм рт.ст. (на відміну від більш бажаного методу P XY/T, який дозволяє уникнути необхідності коригування розрахункового коефіцієнта активності рідини\(\gamma \nonumber\) для зміни температури), з міркувань їх лабораторного обладнання та спрощення їх процедури; і збирати лише один набір даних T XY/P.

Якщо розглядати лише вихідні дані, здається, що криві T- X і T- Y не можуть взаємно перетинатися на осі STC, або що перетин вище очікуваної температури 56,2° C, представника випаровування STC при 740 мм рт.ст. Причина полягає в тому, що точність окремих точок даних низька в області осі STC.

Однак, при згладжуванні даних та екстраполяції кривих T- X та T- Y за допомогою деякої підгонки кривої електронної таблиці, дві криві, здається, цілком ймовірно, що обидві перетинають вісь STC поблизу очікуваної температури 56,2° C. Однак на осі TCS крива підгонка даних T- X і T- Y призводить до їх перетину на осі TCS при 30,0° C, на відміну від очікуваних 32,3° C для чистого TCS. Найбільш імовірним поясненням цієї розбіжності набору даних є те, що зразок TCS, що поставляється, був або непропорційною сумішшю DCS/TCS/STC як отримано, та/або рідини в обладнанні непропорційовані внаслідок будівельних матеріалів обладнання. Температура осі TCS 30,0° C є репрезентативною для рідкої суміші 5% DCS/ 95% TCS. Дивно, але аналітична процедура дослідників не підхопила пік DCS, який би виявив корупцію вибірки (але це поширена помилка, використовуючи цей тип аналізатора дослідника).

Тепер, коли набір даних був дискредитуваний, залишається зрозуміти, що - якщо така - корисна інформація може бути витягнута. Окрім демонстрації техніки, мало користі для зменшення даних, які є високими у «поганих TCS», щоб отримати\(\gamma \nonumber\) асимптоту, що перетинає вісь TCS. Це пов'язано з тим, що мольні фракції X _TCS* змінюються вздовж кривої коефіцієнта активності STC (близько високого співвідношення DCS/TCS 1:19, знижуючись у співвідношенні до дуже мало DCS у потрійній суміші, близькій до 56,2° C на осі STC). Неможливо було б здогадатися, які значення властивостей найкраще використовувати для коефіцієнтів невибагливості, враховуючи вміст DCS «wild-card»). Дані, найближчі до перетину осі STC, можуть бути інтерпольовані, щоб скласти кілька «псевдоточок», близьких до X _TCS = 0, щоб отримати грубе значення\(\gamma \nonumber\) асимптоти TCS (виходячи з припущення, що в трійковій суміші в цій точці мало DCS). Однак навіть невеликі кількості DCS поблизу площі X _TCS = 0 можуть мати значний ефект коефіцієнта активності рідини, і значення нечіткості можуть бути дещо помилковими, припускаючи лише значення властивостей TCS.

Однак, щоб проілюструвати техніку зменшення даних для даних T XY/P (на відміну від бажаної форми P XY/T), кілька «псевдоточок» оцінюються поблизу осі.

Використовуючи криву четвертого порядку, з температурою осі STC, встановленою на 56.20° C, рівняння кривої посадки T- X і T-Y відповідно через функції підгонки кривої таблиці:

Т- Х\(T=18.949x^4-64.825x^3+75.709x^2-56.044x+ 56.20 \nonumber\)

Т- У\(T=-22.243y^4+33.158y^3-18.028y^2-19.075y+ 56.20 \nonumber\)

З цих двох кривих підходів обчислюються наступні «псевдоточки» шляхом вирішення квартичних рівнянь для T- X і T- Y:

Таблиця 8-1, три «псевдоточки», зроблені з кривих прилягання біля осі STC

P, мм рт.ст	Т, °C	Х ТС*	\(\gamma \nonumber\)ТС*
740	56.2	0,0000	\ (\ гамма\ nonnumber\) TCS*» valign="top» width="174" клас = «lt-eng-8146"> 0,0000
740	55.0	0,00359	\ (\ гамма\ nonnumber\) TCS*» valign="top» width="174" клас = «lt-eng-8146"> 0.0104
740	54.0	0.0415	\ (\ гамма\ nonnumber\) TCS*» valign="top» width="174" клас = «lt-eng-8146"> 0,1065
740	53.0	0.0620	\ (\ гамма\ nonnumber\) TCS*» valign="top» width="174" клас = «lt-eng-8146"> 0,1515

У таблиці 8-1 X _TCS* та Y _TCS* підписуються як «TCS*», щоб позначити, що, хоча властивості TCS використовуються для оцінки тиску пари та неміцності, більш летюча рідина насправді суміш DCS/TCS. Точка даних у X, Y = 0,0000, 0.0000 дається лише для того, щоб показати перетин осі STC, але не може бути використана для обчислення\(\gamma \nonumber\) асимптоти, оскільки це призведе до «ділення на нуль» у рівнянні 7-1.

Використовуючи властивості TCS, значення для VP, ø _L і ø _v розраховуються відповідно до частин IV, V і VI, а результати наведені в таблиці 8-2 для розрахункової\(\gamma \nonumber\) _ТС* при 740мм рт.ст. (для кожної «псевдоточкової» температури).

Таблиця 8-2 для\(\gamma \nonumber\) розрахункових ТС* при «псевдоточкових» температурах, з даних PXY/T

P, мм рт.ст	Т, °C	Віце-президент TCS*	Ø L	ø v	\(\gamma \nonumber\)ТС*
740	56.2	2.130	0,9983	1.0321	\ (\ гамма\ nonnumber\) TCS*» valign="top» width="126"> буде визначено
740	55.0	2.055	0,9984	1.0316	\ (\ гамма\ nonnumber\) TCS*» valign="top» width="126"> 1.418
740	54.0	1.994	0,9984	1.0311	\ (\ гамма\ nonnumber\) TCS*» valign="top» width="126"> 1.294
740	53.0	1.934	0,9984	1.0307	\ (\ гамма\ nonnumber\) TCS*» valign="top» width="126"> 1.270

Розрахункові значення для\(\gamma \nonumber\) _TCS* у таблиці 8-2 базуються на X, Y «псевдоточках» таблиці 8-1 та з використанням E quation (\ ref {8-1}) вище, щоб продемонструвати методологію експериментального зменшення даних. Тенденція на коефіцієнти невимушеності та коефіцієнт активності правильна: ø значення _L збільшуються до єдності, оскільки X _TCS* збільшується до єдності; ø _v значення зменшуються до єдності, оскільки X _TCS* збільшується до єдності;\(\gamma \nonumber\) Значення _TCS* зменшуються до єдності, оскільки X _TCS* збільшується до єдності.

Асимптоту на осі СТК визначають шляхом екстраполяції значення\(\gamma \nonumber\) _ТС* з трьох «псевдоточок». (Ця крива мала б інший нахил щодо складу, якби це були дані T XY/P, оскільки температура змінюється так само, як і X _TCS* в таблиці 7-2.) Цей метод ідентифікує асимптоту\(\gamma \nonumber\) _TCS* як 1.437 (середнє значення\(\gamma \nonumber\) _TCS*, отримане шляхом екстраполяції кривих прилягання\(\gamma \nonumber\) _TCS* проти X _TCS* до нульового значення X _TCS*, і \(\gamma \nonumber\)_TCS* проти Y _TCS* до нульового значення X _TCS*). Порівняно з даними інших дослідників, розрахункова асимптота має велике значення. Це також здається високим за очікуванням від рівняння 7-3 з частини VII, що вказувало б на значення, ближче до 1,21 при 56,2° C, або 1,23 @ 32,3° C (очікувана температура кипіння TCS при 740 мм рт.ст.). Можливо, є помилка вмісту DCS, яка, як правило, робить розрахункові значення\(\gamma \nonumber\) _TCS* високими за рахунок збільшення мольної фракції, що не є STC в парі. Методика встановлення кривої може бути «вимкнена», оскільки у двох парах даних, близьких до осі X _TCS* = 0, була низька точність.

Це демонструє, що просто немає хорошого способу «виправити» дані, які мають систематичну помилку в ньому: практично всі тексти говорять про те, що при зіткненні з пошкодженими даними безглуздо продовжувати аналіз даних. На додаток до визначення розумних асимптотичних значень на будь-якій осі, Рейд, Праусніц і Шервуд припускають у «Властивості газів і рідин», що всі\(\gamma \nonumber\) розрахункові значення спочатку регулюються на загальну температурну основу (використовуючи наближення\(Ln(\gamma) \times = constant \nonumber\)), а потім використовувати Гіббса- Закон Дюма для встановлення термодинамічної консистенції. Хоча технічно найкращий спосіб перевірки даних для узгодженості, він вимагає значної кількості високоякісних даних, і пропонується лише в тому випадку, якщо слід враховувати вдосконалені моделі коефіцієнтів активності рідини (наприклад, NRTL або UNIQUAC). Для Ван Лаара, Маргулеса, Вілсона або подібних двоконстантних моделей достатньо 15-20 точок даних.

Завжди краще мати менше точок даних, але мати набір даних внутрішньо узгоджений, а не велика кількість можливих пошкоджених точок даних.

У статті запропоновано використовувати модель Ван Лаара для коефіцієнтів активності, заснованих на обґрунтованих результатах з аналізом даних про хлоросилани, та успіх у прогнозуванні констант Ван Лаара за допомогою рівняння 7-3 у частині VII. Однак читач може захотіти вивчити інші моделі для кращого пристосування до експериментальних даних після підтвердження таких даних. У «Властивостях газів та рідин» автори дають вичерпний перелік інших моделей коефіцієнтів активності, які слід розглянути, з деякими примітками щодо «pro & con».