4.4: Ламіновані композитні плити

Вступ

Цей документ призначений для окреслення механіки армованих волокном ламінованих плит, що призводить до обчислювальної схеми, яка пов'язує внутрішньоплощинну деформацію і кривизну ламінату з накладеними на нього тягами і згинальними моментами. Хоча це невелика частина загальної області композитів, армованих волокном, або навіть теорії ламінату, це важлива техніка, яку повинні розуміти всі інженери композитів.

У наступних розділах ми розглянемо конституційні відносини для ізотропних матеріалів у матричній формі, а потім покажемо, що розширення до поперечно-ізотропних композитних пластин дуже просте. Оскільки кожен шар в ламінаті може бути орієнтований довільно, то ми потім покажемо, як еластичні властивості окремих ламінат можуть трансформуватися в загальний напрямок. Нарешті, ми збалансуємо напруження окремих шарів проти застосованих тяг і моментів, щоб розробити матричні відносини, що регулюють для ламінату в цілому.

Розрахунки для механіки ламінату найкраще проводити за допомогою комп'ютера, а алгоритми окреслені для еластичних ламінатів, ламінатів, що демонструють ефекти теплового розширення, та ламінатів, що демонструють в'язкопружну реакцію.

Ізотропні лінійні еластичні матеріали

Як показано в елементарних текстах з механіки матеріалів (пор. Roylance 1996 (див. Посилання, наведені в кінці цього документа)), декартові деформації, що виникають внаслідок стану плоского напруження ($\sigma_z = \tau_{xz} = \tau_{yz} = 0$), є

$\gamma_{xy} = \dfrac{1}{G} \tau_{xy}$

У плоскому напруженні також є деформація в$z$ напрямку через ефект Пуассона:$\epsilon_z = -\nu (\sigma_x + \sigma_y)$; цей компонент деформації буде ігноруватися в секціях, які слід дотримуватися. У вищезазначених співвідношеннях є три константи пружності: модуль Юнга$E$$\nu$, коефіцієнт Пуассона та модуль зсуву$G$. Однак для ізотропних матеріалів існує лише дві незалежні пружні константи, і, наприклад,$G$ можуть бути отримані з$E$ і$\nu$ як

$G = \dfrac{E}{2(1 + \nu)}$

Використовуючи матричні позначення, ці відносини можуть бути записані як

$$\left \{ \begin{array} {c} {\epsilon_x} \\ {\epsilon_x} \\ {\gamma_{xy}} \end{array} \right \} = \begin{bmatrix} 1/E & -\nu/E & 0 \\ -\nu/E & 1/E & 0 \\ 0 & 0 & 1/G \end{bmatrix} \left \{ \begin{array} {c} {\sigma_x} \\ {\sigma_y} \\ {\tau_{xy}} \end{array} \right \}$$

Величина в дужках називається матрицею відповідності матеріалу, позначається$S$ або$S_{ij}$. Важливо зрозуміти фізичну значимість різних його термінів. Безпосередньо з правил множення матриці елемент в$i^{th}$ рядку і$j^{th}$ стовпці$S_{ij}$ - це внесок$j^{th}$ напруги в$i^{th}$ деформацію. Наприклад, компонент у положенні 1,2 є внеском напруги -напрямку до деформації$y$ -напрямку:$\sigma_y$ множення на$1/E$ дає деформацію$x$ -direction, породжену$\sigma_y$, а потім множення цього на$-\nu$ дає деформацію Пуассона$y$ індукований в$x$ напрямку. Нульові елементи показують відсутність зчеплення між нормальними та зсувними компонентами.

Якщо ми хочемо записати напруження через деформації, рівняння 4.4.1 можна інвертувати, щоб дати:

$$\left \{ \begin{array} {c} {\sigma_x} \\ {\sigma_y} \\ {\tau_{xy}} \end{array} \right \} = \dfrac{E}{1- \nu^2} \begin{bmatrix} 1 & \nu & 0 \\ \nu & 1 & 0 \\ 0 & 0 & (1 - \nu)/2 \end{bmatrix} \left \{ \begin{array} {c} {\epsilon_x} \\ {\epsilon_y} \\ {\gamma_{xy}} \end{array} \right \}$$

де тут$G$ був замінений$E/2(1 + \nu)$. Це відношення може бути скорочено далі як:

$$\sigma = D \epsilon$$

де$D = S^{-1}$ - матриця жорсткості. Відзначимо, що модуль Юнга можна відновити, приймаючи зворотний елемент 1,1 матриці відповідності$S$, але що положення 1,1 матриці жорсткості$D$ містить ефекти Пуассона і не дорівнює$E$.

анізотропні матеріали

Якщо матеріал має текстуру, таку як дерево або однонаправлено армовані волокнисті композити, як показано на малюнку 1, модуль пружності$E_1$ у напрямку волокна, як правило, буде більшим, ніж у поперечних напрямках ($E_2$і$E_3$). Коли$E_1 \ne E_2 \ne E_3$, матеріал, як кажуть, ортотропний. Однак загальним є те, що властивості в площині, поперечній до напрямку волокна, щоб бути ізотропними до хорошого наближення ($E_2 = E_3$); такий матеріал називається поперечно-ізотропним. Пружні конститутивні закони повинні бути змінені з урахуванням цієї анізотропії, а наступна форма є продовженням звичайних рівнянь ізотропної пружності до поперечно-ізотропних матеріалів:

$$\left \{ \begin{array} {c} {\epsilon_1} \\ {\epsilon_2} \\ {\gamma_{12}} \end{array} \right \} = \begin{bmatrix} 1/E_1 & -\nu_{21}/E_2 & 0 \\ -\nu_{12}/E_1 & 1/E_2 & 0 \\ 0 & 0 & 1/G_{12} \end{bmatrix} \left \{ \begin{array} {c} {\sigma_1} \\ {\sigma_2} \\ {\tau_{12}} \end{array} \right \}$$

Малюнок 1: Ортотропний матеріал.

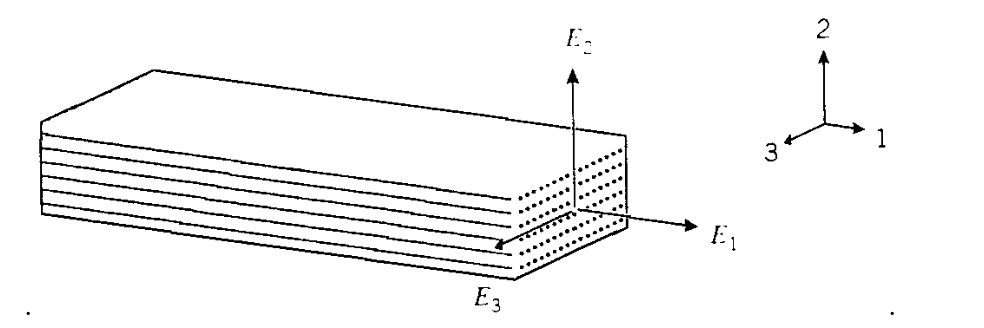
Параметр$\nu_{12}$ є основним коефіцієнтом Пуассона; це відношення деформації, індукованої у напрямку 2 деформацією, застосованою в 1-напрямку. Цей параметр не обмежується значеннями менше 0,5, як в ізотропних матеріалах. І навпаки,$\nu_{21}$ дає деформацію, індуковану в 1-напрямку деформацією, застосованою у напрямку 2. Оскільки 2-напрямок (поперечний до волокон), як правило, має набагато меншу жорсткість, ніж 1-напрямок, дана деформація в напрямку 1 зазвичай розвиває набагато більшу деформацію в напрямку 2, ніж така ж деформація в напрямку 2 індукує деформацію в напрямку 1. Отже, ми, як правило, матимемо$\nu_{12} > \nu_{21}$. У вищенаведеному рівнянні є п'ять констант ($E_1, E_2, \nu_{12}, \nu_{21}$і$G_{12}$. Однак тільки чотири з них незалежні; оскільки$S$ матриця симетрична, ми маємо$\nu_{21}/E_2 = \nu_{12}/E_1$.

Проста форма Рівняння 4.4.4, з нулями в термінами, що представляють зв'язок між нормальною та зсувною складовими, виходить лише тоді, коли осі вирівняні по основним напрямкам матеріалу; тобто уздовж і поперечно до осей волокон. Якщо осі орієнтовані по якомусь іншому напрямку, всі терміни матриці відповідності будуть заповнені, і симетрія матеріалу не буде кидатися в очі. Якщо, наприклад, напрямок волокна знаходиться поза віссю від напрямку завантаження, матеріал буде розвивати деформацію зсуву, коли волокна намагаються зорієнтуватися вздовж напрямку завантаження. Тому буде зв'язок між нормальним напруженням і деформацією зсуву, яка не відбувається в ізотропному матеріалі.

Трансформація осей

Важливо вміти перетворювати осі в «лабораторний»$x - y$ каркас і з нього на каркас з натурального матеріалу, в якому осі можуть бути марковані 1 - 2, що відповідають волокну та поперечним напрямкам, як показано на малюнку 2.

Малюнок 2: Обертання осей.

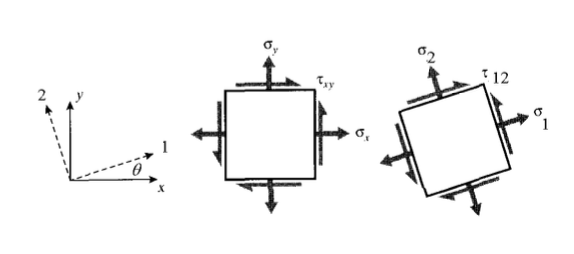
Як показано в елементарних підручниках, закон трансформації для декартового наголосу Коші можна записати:

$$\begin{array} {rcl} {\sigma_1} & = & {\sigma_x \cos^2 \theta + \sigma_y \sin^2 \theta + 2 \tau_{xy} \sin \theta \cos \theta} \\ {\sigma_2} & = & {\sigma_x \sin^2 \theta + \sigma_y \cos^2 \theta - 2 \tau_{xy} \sin \theta \cos \theta} \\ {\tau_{12}} & = & {(\sigma_y - \sigma_x) \sin \theta \cos \theta + \tau_{xy} (\cos^2 \theta -\sin^2 \theta)} \end{array}$$

Де$\theta$ - кут від$x$ осі до осі 1 (волокна). Ці відносини можуть бути записані в матричному вигляді як

$$\left \{ \begin{array} {c} {\sigma_1} \\ {\sigma_2} \\ {\tau_{12}} \end{array} \right \} = \dfrac{E}{1- \nu^2} \begin{bmatrix} c^2 & s^2 & 2sc \\ s^2 & c^2 & -2sc \\ -sc & sc & c^2 - s^2 \end{bmatrix} \left \{ \begin{array} {c} {\sigma_x} \\ {\sigma_y} \\ {\tau_{xy}} \end{array} \right \}$$

де$c = \cos \theta$ і$s = \sin \theta$. Це може бути скорочено як

$$\sigma' = A \sigma$$

де$A$ матриця перетворення в дужках вище. Цей вираз може бути застосований як до тривимірних, так і двовимірних напружених станів, хоча конкретна форма,$A$ наведена в рівнянні 4.4.6, дійсна лише у двох вимірах (плоска напруга) та для декартових координат.

Використовуючи математичні або геометричні аргументи, можна показати, що компоненти нескінченно малої деформації трансформуються майже однаковими співвідношеннями:

$$\left \{ \begin{array} {c} {\epsilon_1} \\ {\epsilon_2} \\ {\tfrac{1}{2} \gamma_{12}} \end{array} \right \} = A \left \{ \begin{array} {c} {\epsilon_x} \\ {\epsilon_y} \\ {\tfrac{1}{2} \gamma_{xy}} \end{array} \right \}$$

Коефіцієнт 1/2 на складових зсуву виникає з класичного визначення деформації зсуву, яка вдвічі перевищує тензоріальну деформацію зсуву. Це вносить деяку незручність в трансформаційні відносини, які можна зменшити, вводячи матрицю Рейтера, визначену як

$$[R] = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{bmatrix} \ \ or \ \ [R]^{-1} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & \tfrac{1}{2} \end{bmatrix}$$

Тепер ми можемо написати:

$\left \{ \begin{array} {c} {\epsilon_1} \\ {\epsilon_2} \\ { \gamma_{12}} \end{array} \right \} = R \left \{ \begin{array} {c} {\epsilon_1} \\ {\epsilon_2} \\ {\tfrac{1}{2} \gamma_{12}} \end{array} \right \} = RA \left \{ \begin{array} {c} {\epsilon_x} \\ {\epsilon_y} \\ {\tfrac{1}{2} \gamma_{xy}} \end{array} \right \} = RAR^{-1} \left \{ \begin{array} {c} {\epsilon_x} \\ {\epsilon_y} \\ {\gamma_{xy}} \end{array} \right \}$

або

$$\epsilon' = RAR^{-1} \epsilon$$

Закон трансформації для комплаєнсу тепер може бути розроблений з законів трансформації для деформацій і стресів. Послідовними перетвореннями деформація в$x-y$ довільному напрямку пов'язана з деформацією в 1-2 (основний матеріал) напрямках, потім до напружень в 1-2 напрямках і, нарешті, до напружень в$x-y$ напрямках. Остаточною групуванням матриць перетворення, що стосуються$x-y$ деформацій до$x-y$ напружень, є перетворена матриця відповідності в$x-y$ напрямку:

$\left \{ \begin{array} {c} {\epsilon_x} \\ {\epsilon_y} \\ { \gamma_{xy}} \end{array} \right \} = R \left \{ \begin{array} {c} {\epsilon_x} \\ {\epsilon_y} \\ {\tfrac{1}{2} \gamma_{xy}} \end{array} \right \} = RA^{-1} \left \{ \begin{array} {c} {\epsilon_1} \\ {\epsilon_2} \\ {\tfrac{1}{2} \gamma_{12}} \end{array} \right \} = RA^{-1} R^{-1} \left \{ \begin{array} {c} {\epsilon_1} \\ {\epsilon_2} \\ { \gamma_{12}} \end{array} \right \}$

$=RA^{-1} R^{-1} S \left \{ \begin{array} {c} {\sigma_1} \\ {\sigma_2} \\ { \tau_{12}} \end{array} \right \} = RA^{-1} R^{-1} SA \left \{ \begin{array} {c} {\sigma_x} \\ {\sigma_y} \\ { \tau_{xy}} \end{array} \right \} \equiv \bar{S} \left \{ \begin{array} {c} {\sigma_x} \\ {\sigma_y} \\ { \tau_{xy}} \end{array} \right \}$

де$\bar{S}$ - перетворена матриця відповідності щодо$x-y$ осей. Зворотний від$\bar{S}$ is$\bar{D}$, матриця жорсткості щодо$x-y$ осей:

$$\bar{S} = RA^{-1} R^{-1} SA, \ \ \bar{D} = \bar{S}^{-1}$$

Приклад$\PageIndex{1}$

Розглянемо шар кевлар-епоксидного композиту з жорсткістю$E_1 = 82, E_2 = 4, G_{12} = 2.8$ (всі ГПа) і$\nu_{12} = 0.25$. орієнтований на$30^{\circ}$ від$x$ осі. Жорсткість у$x$ напрямку можна знайти як зворотну елементу 1,1 перетвореної матриці відповідності$S$, як дано рівнянням 4.4.11. Нижче показано, як це можна зробити за допомогою символічного математичного програмного забезпечення Maple (відредаговано для стислості):

Read linear algebra package
> with(linalg):
Define compliance matrix
> S:=matrix(3,3,[[1/E[1],-nu[21]/E[2],0],[-nu[12]/E[1],1/E[2],0],[0,0,1/G[12]]]); 
Numerical parameters for Kevlar-epoxy
> Digits:=4;unprotect(E);E[1]:=82e9;E[2]:=4e9;G[12]:=2.8e9;nu[12]:=.25; 
nu[21]:=nu[12]*E[2]/E[1];
Compliance matrix evaluated
> S2:=map(eval,S); 

$S2 := \begin{bmatrix} .122010^{-10} & -.305010^{-11} & 0 \\ -.304910^{-11} & .250010^{-9} & 0 \\ 0 & 0 & .357110^{-9} \end{bmatrix}$

Transformation matrix
> A:=matrix(3,3,[[c^2,s^2,2*s*c],[s^2,c^2,-2*s*c],[-s*c,s*c,c^2-s^2]]); 
Trigonometric relations and angle
> s:=sin(theta);c:=cos(theta);theta:=30*Pi/180;
Transformation matrix evaluated
> A2:=evalf(map(eval,A)); 

$A2 := \begin{bmatrix} .7500 & .2500 & .8660 \\ .2500 & .7500 & -.8660 \\ -.4330 & .4330 & .5000 \end{bmatrix}$

Reuter's matrix
> R:=matrix(3,3,[[1,0,0],[0,1,0],[0,0,2]]);
Transformed compliance matrix
> Sbar:=evalf(evalm( R &* inverse(A2) &* inverse(R) &* S2 &* A2 )); 

$Sbar := \begin{bmatrix} .882810^{-10} & -.196810^{-10} & -.122210^{-9} \\ -.196910^{-10} & .207110^{-9} & -.837010^{-10} \\ -.122210^{-9} & -.837710^{-10} & .290510^{-9} \end{bmatrix}$

Stiffness in x-direction
> 'E[x]'=1/Sbar[1,1]; 

$E_x = .113310^{11}$

Зверніть увагу, що перетворена матриця відповідності симетрична (до числової помилки округлення), але існують ненульові значення зв'язку. Користувач, який не знає про внутрішній склад матеріалу, вважав би його повністю анізотропним.

Ламіновані композитні плити

Однією з найбільш поширених форм армованих волокном композитних матеріалів є перехресний ламінат, в якому виробник «закладає» послідовність односпрямованих армованих «шарів», як зазначено на малюнку 3. Кожен шар, як правило, являє собою тонкий (приблизно 0,2 мм) лист колімованих волокон, просочений неотвержденной епоксидною смолою або іншим термореактивним полімерним матричним матеріалом. Орієнтація кожного шару довільна, а послідовність укладання підібрана для досягнення бажаних властивостей ламінату. У цьому розділі ми описуємо, як розробляються та аналізуються такі ламінати.

Малюнок 3:3-шаровий симетричний ламінат.

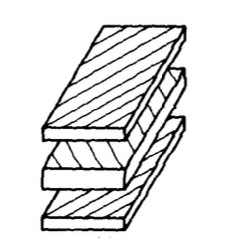
\ Класична теорія ламінату» є продовженням теорії згинання однорідних пластин, але з урахуванням внутрішньоплоских тяг на додаток до згинальних моментів, і для різної жорсткості кожного шару при аналізі. У загальних випадках визначення тяг і моментів в заданому місці зажадає вирішення загальних рівнянь для рівноваги і зміщення сумісності пластин. Ця теорія розглядається в ряді стандартних текстів (пор. С.Тимошенко і С.Войновський-Крігер, Теорія плит і раковин, Макгроу-Хілл, Нью-Йорк, 1959 р.), і тут обговорюватися не буде.

Почнемо з того, що припускаємо знання тяг N і моментів M, застосованих до пластини в положенні$x,y$, як показано на малюнку 4:

$$N = \left \{ \begin{array} {c} {N_x} \\ {N_y} \\ {N_{xy}} \end{array} \right \} \ \ \ M = \left \{ \begin{array} {c} {M_x} \\ {M_y} \\ {M_{xy}} \end{array} \right \}$$

Малюнок 4: Застосовані моменти при згинанні пластини.

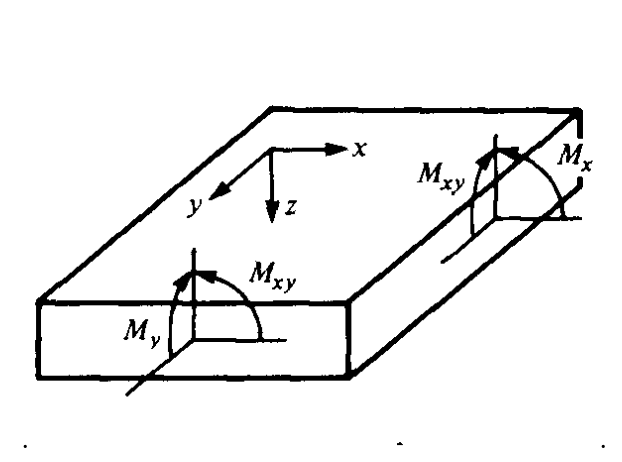
Зручно буде нормалізувати ці тяги і моменти по ширині плити, так вони мають одиниці$N/m$ і$N-m/m$, або просто$N$ відповідно. Координати$x$ і$y$ є напрямками в площині плити, і$z$ прийнято приймати як позитивні вниз. Прогин в$z$ напрямку називається$w$, також приймається як позитивний вниз.

Малюнок 5: Зсув точки в тарілці (з Пауелла, 1983).

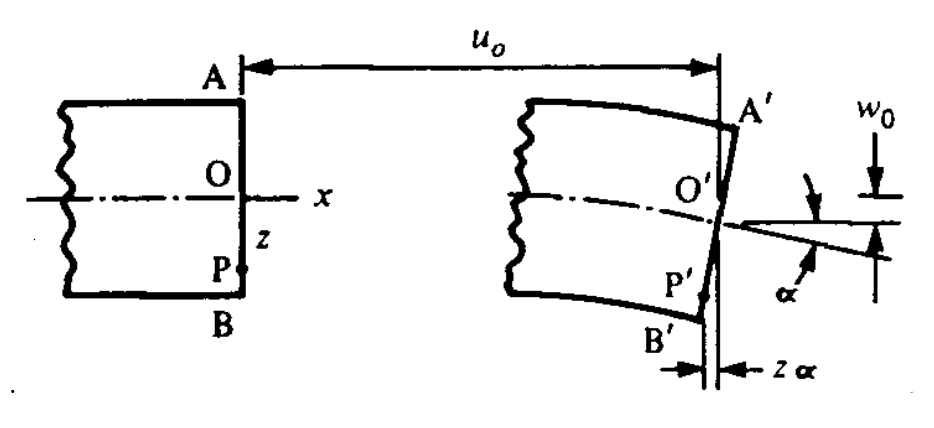
Аналогічно з припущенням Ейлера для балок, припущення Кіршкофа для згинання пластини приймає спочатку прямі вертикальні лінії, щоб залишатися прямими, але обертатися навколо середньої площини ($z = 0$). Як показано на малюнку 5, горизонтальні зсуви$u$ і$v$ в$y$ напрямках$x$ і за рахунок обертання можуть бути прийняті до розумного наближення від кута повороту і відстані від середньої площини, і це обертальне переміщення додається до зміщення середньої площини ( $u_0, v_0$):

$$u = u_0 - z w_{0, x}$$

$$v = v_0 - z w_{0, y}$$

$$\epsilon = \left \{ \begin{array} {c} {\epsilon_x} \\ {\epsilon_y} \\ { \gamma_{xy}} \end{array} \right \} = \left \{ \begin{array} {c} {u_{,x}} \\ {v_{,y}} \\ {u_{,y} + v_{,x}} \end{array} \right \} = \left \{ \begin{array} {c} {u_{0,x} - zw_{0,xx}} \\ {v_{0,y} - zw_{0, yy}} \\ {(u_{0,y} + v_{0, x}) - 2z w_{0, xy}} \end{array} \right \} = \epsilon^0 + z\kappa$$

Штами є лише градієнтами переміщень; використовуючи матричні позначення їх можна записати, де$\epsilon^0$ знаходиться деформація середньої площини і$\kappa$ є вектором других похідних зміщення, що називається кривизною:

$\kappa = \left \{ \begin{array} {c} {\kappa_x} \\ {\kappa_y} \\ { \kappa_{xy}} \end{array} \right \} = \left \{ \begin{array} {c} {-w_{0, xx}} \\ {-w_{0, yy}} \\ {-2w_{0, xy}} \end{array} \right \}$

Компонент$\kappa_{xy}$ являє собою скручувальну кривизну,$x$ вказуючи, як змінюється нахил середньої площини$y$ -direction$y$ (або еквівалентно, як змінюється нахил напрямку$x$).

Напруження щодо$x-y$ осей тепер визначаються з деформацій, і при цьому потрібно враховувати, що кожен шар взагалі матиме різну жорсткість, залежно від власних властивостей, а також своєї орієнтації щодо$x-y$ осей. Це враховується шляхом обчислення перетвореної матриці жорсткості$\bar{D}$, як описано в попередньому розділі (Equation 4.4.11). Нагадаємо, що жорсткість шару, задана рівнянням 4.4.4, - це ті, що вздовж волокна та поперечні напрямки цього конкретного шару. Властивості кожного шару необхідно трансформувати в загальні$x-y$ осі, підібрані довільно для всього ламінату. Напруги при будь-якому вертикальному положенні тоді:

$$\sigma = \bar{D} \epsilon = \bar{D} \epsilon^0 + z \bar{D} \kappa$$

де тут$\bar{D}$ трансформована жорсткість шару в положенні, при якому обчислюються напруги.

Кожен з цих шарів напружень повинен додати, щоб збалансувати тягу на одиницю ширини$N$:

$$N = \int_{-h/2}^{+h/2} \sigma dz = \sum_{k = 1}^{N} \int_{z_k}^{z_{k + 1}} \sigma_k dz$$

де$\sigma_k$ напруга в$k$ шарі і$z_k$ відстань від середини ламінату до$k$ нижньої частини шару. Використання рівняння 4.4.16 для запису напружень через деформації та кривизни середньої площини:

$$N = \sum_{k = 1}^{N} (\int_{z_k}^{z_{k + 1}} \bar{D} \epsilon^0 dz + \int_{z_k}^{z_{k + 1}} \bar{D} \kappa z dz)$$

Кривизна$\kappa$ і деформація середньої площини$\epsilon^0$ є постійними протягом усього$z$, і перетворена жорсткість$\bar{D}$ не змінюється в межах заданого шару. Видалення цих величин зсередини інтегралів:

$$N = \sum_{k = 1}^{N} (\bar{D} \epsilon^0 \int_{z_k}^{z_{k + 1}} dz + \bar{D} \kappa \int_{z_k}^{z_{k + 1}} z dz)$$

Після оцінки інтегралів цей вираз можна записати в компактному вигляді:

$$N = \mathcal{A} \epsilon^0 + \mathcal{B} \kappa$$

де$\mathcal{A}$ - «матриця розтягнутої жорсткості», яка визначається як:

$$\mathcal{A} = \sum_{k = 1}^{N} \bar{D} (z_{k + 1} - z_k)$$

і$\mathcal{B}$ являє собою «матрицю жорсткості зчеплення», яка визначається як:

$$\mathcal{B} = \dfrac{1}{2} \sum_{k = 1}^{N} \bar{D} (z_{k + 1}^2 - z_k^2)$$

Обґрунтування назв «extensional» і «couption» запропоновано рівнянням 4.4.20. $\mathcal{A}$Матриця дає вплив розтягнутої середньої площини деформації$\epsilon^0$ на внутрішню тягу$N$, а$\mathcal{B}$ матриця дає внесок кривизни$\kappa$ в тягу. Може бути не очевидно, чому згинання плити зажадає внутрішньоплощинной тяги, або навпаки, чому витягування пластини в її площині призведе до її згинання. Але візуалізуйте пластину, що містить шари все тієї ж жорсткості, за винятком деяких дуже низькомодульних шарів десь над її середньою площиною. Коли пластина витягується, більш сумісні шари над середньою площиною, як правило, розтягуються більше, ніж жорсткіші шари нижче середньої площини. Верхня половина ламінату тягнеться більше, ніж нижня половина, тому вона приймає увігнуто-вниз кривизну.

Аналогічно, результуючі моменти на одиницю ширини повинні врівноважуватися моментами, що сприяють внутрішнім напруженням:

$$M = \int_{-h/2}^{+h/2} \sigma z dz = \mathcal{B} \epsilon^0 + \mathcal{D} \kappa$$

де$\mathcal{D}$ «матриця жорсткості на вигин» визначається як:

$$\mathcal{D} = \dfrac{1}{3} \sum_{k = 1}^{N} \bar{D} (z_{k + 1}^3 - z_k^3)$$

Повний набір зв'язків між прикладними силами та моментами, а також отримані деформації та кривизни середньої площини можна узагальнити як єдине матричне рівняння:

$$\left \{ \begin{array} {c} {N} \\ {M} \end{array} \right \} = \begin{bmatrix} \mathcal{A} & \mathcal{B} \\ \mathcal{B} & \mathcal{D} \end{bmatrix} \left \{ \begin{array} {c} {\epsilon^0} \\ {\kappa} \end{array} \right \}$$

$\mathcal{A}/\mathcal{B}/\mathcal{B}/\mathcal{D}$Матриця в дужках - це матриця жорсткості ламінату, а її зворотним буде матриця відповідності ламінату.

Наявність ненульових елементів в матриці зчеплення$\mathcal{B}$ вказує на те, що застосування в площині тяги призведе до викривлення або викривлення пластини, або що прикладений згинальний момент також буде генерувати подовжувальну деформацію. Ці ефекти, як правило, небажані. Однак їх можна уникнути, зробивши ламінат симетричним щодо середньої площини, як може виявити експертиза Рівняння 4.4.22. (У деяких випадках ця муфта подовжувач-кривизна може бути використана як цікава конструктивна особливість. Наприклад, можна сконструювати композитну лопатку гвинта, кут атаки якого автоматично змінюється зі швидкістю обертання: збільшена швидкість збільшує доцентрове навантаження в площині, що викликає скручування в лопаті.)

Наведені вище співвідношення забезпечують прямий (хоча і виснажливий, якщо не використовується комп'ютер) засіб визначення напружень і переміщень в ламінованих композиціях, що піддаються внутрішньоплощинним тяговим або згинальним навантаженням:

1. Для кожного типу матеріалу в послідовності укладання отримують шляхом вимірювання або мікромеханічної оцінки чотири незалежних анізотропних параметра, що відображаються в Рівнянні 4.4.4: ($E_1, E_2, \nu_{12}$, і$G_{12}$).

2. Використовуючи Рівняння 4.4.11, перетворіть матрицю відповідності для кожного шару з основних напрямків матеріалу шару на деякі зручні опорні осі, які будуть використовуватися для ламінату в цілому.

3. Інвертувати перетворену матрицю відповідності для отримання перетвореної (щодо$x-y$ осей) матриці жорсткості. $\bar{D}$.

4. Додайте внесок кожного шару до$\mathcal{D}$ матриць$\mathcal{A}, \mathcal{B}$ і, як це передбачено Eqns. 4.4.21, 4.4.22 та 4.4.24.

5. Введіть задані тяги$N$ і згинальні моменти$M$, і сформуйте системні рівняння, задані рівнянням 4.4.25.

6. Розв'яжіть отриману систему для невідомих значень внутрішньоплоского деформації$\epsilon^0$ та кривизни$\kappa$.

7. Використовуйте Рівняння 4.4.16 для визначення напружень шару для кожного шару в ламінаті в перерахунку на$\epsilon^0, \kappa$ і$z$. Це будуть напруги щодо$x - y$ осей.

8. Використовуйте рівняння 4.4.6 для перетворення$x - y$ напружень назад до основних осей матеріалу (паралельних і поперечних волокнам).

9. При бажанні окремі напруження шару можуть бути використані у відповідному критерії відмови для оцінки ймовірності виходу цього шару з ладу. Критерій Цай-Хілла широко використовується для цієї мети:
   $$(\dfrac{\sigma_1}{\hat{\sigma}_1})^2 - \dfrac{\sigma_1 \sigma_2}{\hat{\sigma}_1^2} + (\dfrac{\sigma_2}{\hat{\sigma}_2})^2 + (\dfrac{\tau_{12}}{\hat{\tau}_{12}})^2 = 1$$
   $\hat{\sigma}_2$ Ось$\hat{\sigma}_1$ і міцність на розрив шарів паралельно і вздовж напрямку волокна,$\hat{\tau}_{12}$ а також міцність внутрішньомісячного шару. Цей критерій прогнозує невдачу, коли ліва сторона вищевказаного рівняння дорівнює або перевищує одиницю.

Приклад$\PageIndex{2}$

Аналіз ламінату, описаний вище, був реалізований в коді з назвою пластини, і цей приклад демонструє використання цього коду при визначенні жорсткості двошарового композиту 0/90 графіту/епоксидного композиту. Тут кожному з двох шарів дається товщина 0,5, тому загальна висота ламінату складе одиницю. Теорія ламінату передбачає одиницю ширини, тому загальна жорсткість і відповідність матриць будуть засновані на одиничному перерізі.

> plate
assign properties for lamina type 1...

enter modulus in fiber direction... 
    (enter -1 to stop): 230e9
enter modulus in transverse direction: 6.6e9 
enter principal Poisson ratio: .25
enter shear modulus: 4.8e9
enter ply thickness: .5
assign properties for lamina type 2... 
enter modulus in fiber direction... 
    (enter -1 to stop): -1
define layup sequence, starting at bottom... 
    (use negative material set number to stop)
enter material set number for ply number 1: 1
enter ply angle: 0
enter material set number for ply number 2: 1
enter ply angle: 90
enter material set number for ply number 3: -1

laminate stiffness matrix:

    0.1185E+12  0.1653E+10  0.2942E+04   -0.2798D+11  0.0000D+00  0.7354D+03
    0.1653E+10  0.1185E+12  0.1389E+06    0.0000D+00  0.2798D+11  0.3473D+05
    0.2942E+04  0.1389E+06  0.4800E+10    0.7354D+03  0.3473D+05  0.0000D+00
    
   -0.2798E+11  0.0000E+00  0.7354E+03    0.9876D+10  0.1377D+09  0.2451D+03 
    0.0000E+00  0.2798E+11  0.3473E+05    0.1377D+09  0.9876D+10  0.1158D+05 
    0.7354E+03  0.3473E+05  0.0000E+00    0.2451D+03  0.1158D+05  0.4000D+09 

laminate compliance matrix: 
    
    0.2548E-10 -0.3554E-12 -0.1639E-16    0.7218D-10  0.7125D-19 -0.6022D-16 
   -0.3554E-12  0.2548E-10 -0.2150E-15    0.3253D-18 -0.7218D-10 -0.1228D-15 
   -0.1639E-16 -0.2150E-15  0.2083E-09   -0.6022D-16 -0.1228D-15  0.2228D-19 
   -0.6022E-16 -0.1228E-15  0.2228E-19   -0.1967D-15 -0.2580D-14  0.2500D-08 

Зверніть увагу, що цей несиметричний ламінат генерує ненульові значення в матриці зв'язку$\mathcal{B}$, як і очікувалося. Жорсткість однакова в$x$ і$y$ напрямках, в чому можна переконатися, розглянувши 1,1 і 2,2 елементи матриці відповідності ламінату. Ефективним модулем є$E_x = E_y = 1/0.2548 \times 10^{-10} = 39.2$ ГПа. Однак ламінат не є ізотропним, як це можна виявити шляхом перекатки плити з укладанням 0/90, орієнтованим під іншим кутом від$x - y$ осей.

Температурні ефекти

Існує ряд поліпшень, які можна розглянути для описаного вище коду пластини: він може бути розширений, щоб включити міжламінарні напруги зсуву між шарами, він може включати базу даних комерційно доступних препрегів і основних матеріалів, або користувальницький інтерфейс може бути зроблений\ більш дружнім» і графічно орієнтований. Багато таких функцій доступні в комерційних кодах, або можуть бути додані користувачем, і далі тут не будуть обговорюватися. Однак ефекти теплового розширення настільки важливі в застосуванні, що код ламінату майже повинен мати цю особливість, щоб бути корисним, і загальний підхід буде викладено тут.

Загалом, підвищення температури$\Delta T$ викликає теплове розширення, яке дається відомим співвідношенням$\epsilon_T = \alpha \Delta T$, де$\epsilon_T$ знаходиться термічно індукована деформація і$\alpha$ коефіцієнт лінійного теплового розширення. Ця теплова деформація отримується без необхідності застосування напруги, так що коли закон Гука використовується для обчислення напруги від деформації, спочатку віднімається теплова складова:$\sigma = E(\epsilon - \alpha \Delta T)$. Теплове розширення викликає лише нормальну деформацію, тому зсувні компоненти деформації не впливають. Таким чином, рівняння 4.4.3 може бути розширено як

де вектор теплової деформації в координатній рамці 1 - 2 дорівнює

$\epsilon_T = \left \{ \begin{array} {c} {\alpha_1} \\ {\alpha_2} \\ {0} \end{array} \right \} \Delta T$

Ось$\alpha_1$ і$\alpha_2$ наведені анізотропні коефіцієнти теплового розширення в волоконному і поперечному напрямках. Трансформуючись в загальні$x - y$ осі, це відношення стає:

$$\left \{ \begin{array} {c} {\sigma_x} \\ {\sigma_y} \\ {\tau_{xy}} \end{array} \right \} = \begin{bmatrix} \hat{D}_{11} & \hat{D}_{12} & \hat{D}_{13} \\ \hat{D}_{21} & \hat{D}_{22} & \hat{D}_{23} \\ \hat{D}_{31} & \hat{D}_{32} & \hat{D}_{33} \end{bmatrix} \left \{ \begin{bmatrix} {\epsilon_x} \\ {\epsilon_y} \\ {\epsilon_{xy}} \end{bmatrix} - \begin{bmatrix} {\alpha_x} \\ {\alpha_y} \\ {\alpha_{xy}} \end{bmatrix} \Delta T\right \}$$

Індекси на$\bar{D}$ елементах стосуються позицій рядків та стовпців у матриці жорсткості, а не координатних напрямків; надпланка служить нагадуванням про те, що ці елементи стосуються$x - y$ осей. Вектор теплового розширення на правій стороні ($\alpha = \alpha_x, \alpha_y, \alpha_{xy}$) по суті є вектором деформації, і тому його можна отримати з ($\alpha_1, \alpha_2, 0$), як у Рівнянні 4.4.10:

$\alpha = \left \{ \begin{array} {c} {\sigma_x} \\ {\sigma_y} \\ {\sigma_{xy}} \end{array} \right \} = RA^{-1} R^{-1} \left \{ \begin{array} {c} {\alpha_1} \\ {\alpha_2} \\ {0} \end{array} \right \}$

Зверніть увагу, що в загальному$x - y$ напрямку теплове розширення викликає як нормальні, так і зсувні деформації.

Попереднє незалежне від температури розвиток тепер можна повторити, модифікувавши лише шляхом проведення термінів теплового розширення. Як і раніше, вектор деформації для будь-якого положення$z$ від середньої площини задається через деформацію$\epsilon^0$ та кривизну$\kappa$ середньої площини

$\epsilon = \epsilon^0 + z\kappa$

Відповідний стрес тоді

Врівноваження напружень від застосованих тяг і моментів, як і раніше:

Цей результат ідентичний результату рівняння 4.4.20 та рівняння 4.4.23, крім додавання інтегралів, що представляють «теплові навантаження». Це дозволяє вирішувати проблеми, що залежать від температури, за допомогою «еквівалентної механічної формули»; загальні керуючі рівняння можуть бути записані як

$$\left \{ \begin{array} {c} \bar{N} & \bar{M} \end{array} \right \} = \begin{bmatrix} \mathcal{A} & \mathcal{B} \\ \mathcal{B} & \mathcal{D} \end{bmatrix} \left \{ \begin{array} {c} \epsilon^0 & \kappa \end{array} \right \}, \ \ \ or \ \ \ \left \{ \begin{array} {c} \epsilon^0 & \kappa \end{array} \right \} = \begin{bmatrix} \mathcal{A} & \mathcal{B} \\ \mathcal{B} & \mathcal{D} \end{bmatrix}^{-1} \left \{ \begin{array} {c} \bar{N} & \bar{M} \end{array} \right \}$$

де\ еквівалентні теплові навантаження» задаються як

$\bar{N} = N + \int \bar{D} \alpha \Delta T dz$

$\bar{M} = M + \int \bar{D} \alpha \Delta T z dz$

Розширення коду пластини для розміщення теплових ефектів, таким чином, складається з модифікації вектора навантаження 6$\times$ 1 шляхом додавання двох векторних інтегралів 3$\times$ 1 у вищезгаданому виразі.

В'язкопружні ефекти

Оскільки матриця багатьох композитних ламінатів полімерна, конструктору може знадобитися розглянути можливість в'язкопружного розслаблення напружень або повзучості під час навантаження. Будь-який такий ефект, ймовірно, не буде великим, так як волокна, які несуть більшу частину навантаження, зазвичай не є в'язкоеластичними. Далі матеріал матриці зазвичай використовується значно нижче його температури склопереходу, і буде діяти в склоподібному еластичному режимі.

Однак деякі програми можуть бути не такими простими. Якщо ламінат використовується при підвищеній температурі, і якщо напруги діють в напрямках, не підтримуваних армуючими волокнами, можуть спостерігатися релаксаційні ефекти. На малюнку 6 показана повзучість, виміряна в однонаправленому графіто-епоксидному ламінаті T300/5208 (M.E. Tuttle and H.F. Brinson, «Прогнозування довгострокової відповідності повзучості загальних композитних ламінатів,» Експериментальна механіка, стор. 89, березень 1986.), завантажений поперечно до волокон на 149$^{\circ} C$. Навіть у цьому майже найгіршому випадку деформації повзучості відносно невеликі (менше 10% еластичної деформації), але малюнок 6 показує, що ефекти релаксації можуть бути важливими в деяких ситуаціях.

Малюнок 6: Реакція повзучі/повзучі-відновлення графітово-епоксидного ламінату.

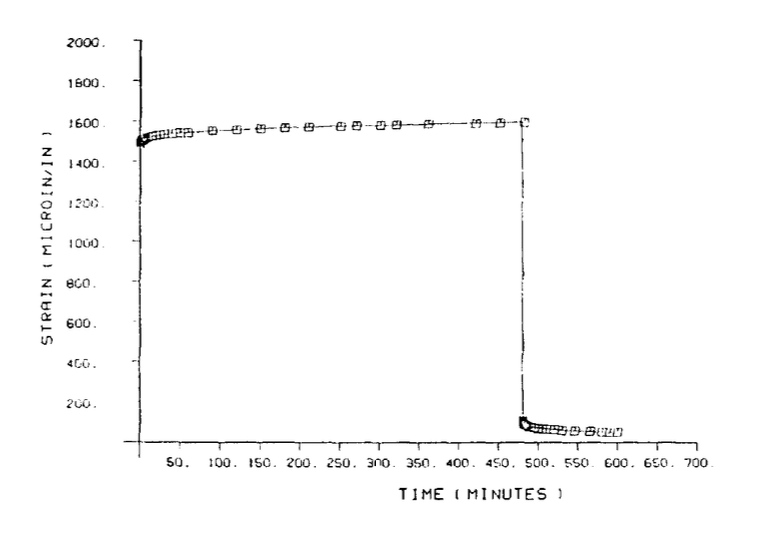
Наведена вище стаття Таттла-Брінсона описує покрокову обчислювальну схему, яка може бути використана для моделювання цих в'язкопружних ефектів ламінату, і тут буде викладена спрощена форма їх методу. В'язкопружна деформація повзучості, що виникає в даному шарі протягом певного приросту часу,$dt$ може бути розрахована на основі напруги в шарі в той час, припускаючи, що шар вільний від сусідніх шарів; це дає незалежний шар деформації повзучості. Цей штам буде діяти, щоб розслабити шаровий стрес.

Звичайно, шари не можуть вільно напружуватися довільно, і належну сумісність деформацій можна відновити шляхом розрахунку зовнішніх навантажень, які б створювали пружні деформації, рівні незалежним шарам повзучості. Ці навантаження підсумовуються по всіх шарах в ламінаті, щоб дати еквівалентну навантаження на повзучість ламінату. Це навантаження застосовується до ламінату для обчислення набору сумісних деформацій і кривизн, які називаються еквівалентним деформацією повзучості ламінату. Ця деформація додається до початкової пружної деформації при обчисленні напруги на заданому шарі, тоді як незалежний шар деформації повзучості віднімається.

Наступний список більш детально розробляє ці кроки:

1. Пружні деформації та кривизни середньої площини вирішуються для заданих згинальних моментів і тяг, використовуючи склоподібні модулі різних шарів. З рівняння 4.4.25:

$\left \{ \begin{array} {c} \epsilon^0 & \kappa \end{array} \right \} = \begin{bmatrix} \mathcal{A} & \mathcal{B} \\ \mathcal{B} & \mathcal{D} \end{bmatrix}^{-1} \left \{ \begin{array} {c} N & M \end{array} \right \}$

2. Потім пружна деформація в кожному шарі отримується з Рівняння 4.4.15. Для шару$k^{th}$, з центром у координаті$z$, це:

$\epsilon_{p\_e\_xy} = \epsilon^0 + z\kappa$

де$p\_e\_xy$ індекси позначають шар, пружний, напруга в$x-y$ напрямку. Штами пружного шару відносно 1-2 (волоконно-поперечних) напрямків задаються перетворенням Рівняння 4.4.10:

$\epsilon_{p\_e\_12} = RAR^{-1} \epsilon_{p\_e\_xy}$

Ці перші два кроки виконуються кодом пружної пластини, а адаптація до в'язкопружної реакції складається з додавання наступних кроків.

3. Поточна напруга шару$\sigma_{k\_12}$ в 1-2 напрямках становить:

Величина$\epsilon_{p\_lc\_12} - \epsilon_{p\_c\_12}$ - це різниця між еквівалентною деформацією повзучості ламінату та незалежним шаром деформації повзучості. Величини$\epsilon_{p\_lc\_12}$ і$\epsilon_{p\_c\_12}$ встановлюються на нуль спочатку, але оновлюються в кроках 4 і 8 нижче, щоб врахувати в'язкопружну релаксацію.

4. Поточне напруження шару в потім використовується у відповідній в'язкопружній моделі для обчислення повзучості, яка виникла б, якби шар вільно деформувався незалежно від сусідніх шарів; це називається незалежною деформацією повзучості шару. Для простої моделі Voigt поточне значення деформації повзучості може бути оновлено з його значення на попередньому часовому кроці як:

де надскрипти на деформації вказують значення на поточному та попередньому кроках часу. $C_v$Ось в'язкопружна відповідність повзучості і$\tau$ час релаксації. Штам повзучості, рівний,$C_v$ буде розвиватися на додаток до початкової еластичної деформації в ламінаті, і частка цієї$2/e$ деформації повзучості буде розвиватися через час$\tau$. Різні значення$C_v$ будуть використані для волокон, поперечних і зсувних деформаційних компонентів через анізотропії шару.

5. Напруження в напрямах 1-2 та\ (x-y), які були б необхідні для розвитку незалежних деформацій повзучості, якщо пласт був пружним, складають

$\sigma_{k\_12} = D\epsilon_{p\_c\_12}$

$\sigma_{k\_xy} = A^{-1} \sigma_{k\_12}$

6. Ці еквівалентні напруження пружного шару підсумовуються над усіма шарами в ламінаті, щоб створити еквівалентну навантаження на повзучість ламінату. Внесок$k^{th}$ п'єса становить:

$N_c = N_c + t_k \sigma_{k\_xy}$

$M_c = M_c + t_k z \sigma_{k\_xy}$

де$k^{th}$ - товщина шару і$k^{th}$ координата його$z$ осьової лінії.

7. Еквівалентна деформація повзучості ламінату потім обчислюється з еластичної матриці відповідності та еквівалентних навантажень на повзучість ламінату як

$\left \{ \begin{array} {c} \epsilon_{lc}^0 & \kappa_{lc} \end{array} \right \} = \begin{bmatrix} \mathcal{A} & \mathcal{B} \\ \mathcal{B} & \mathcal{D} \end{bmatrix}^{-1} \left \{ \begin{array} {c} N_c & M_c \end{array} \right \}$

8. Шарова деформація повзучості ламінату в$x-y$ і 1-2 напрямках

$\epsilon_{p\_pc\_xy} = \epsilon_{lc}^0 + z \kappa_{lc}$

$\epsilon_{p\_lc\_12} = RAR^{-1} \epsilon_{p\_lc\_xy}$

9. Нарешті, час збільшується,$(t \leftarrow t + dt)$ і інший часовий цикл обчислюється, починаючи з кроку 3.

Приклад$\PageIndex{3}$

В якості ілюстрації наведеного алгоритму розглянемо просту модель ламінату з одним ізотропним шаром. Пружні константи є$E = 100$ (довільні одиниці) і$\nu = 0.25$, а одиничне напруження прикладається в$x$ -напрямку. Отже,$x$ початкова деформація напрямку$\epsilon_{x,0} = \sigma_x/E = 0.01$. У цьому ізотропному тесті код обчислює модуль зсуву як$G = E/2(1 + \nu)$. Деформація повзучості регулюється параметром$v_{frac}$, який встановлює відповідність$G_v$ повзучості Voigt$v_{frac}/E_2$ у поперечному напрямку$v_{frac}/G_{12}$ для компонентів зсуву та нуль у напрямку волокна (припускаючи лише еластичну реакцію вздовж волокон).

На малюнку 7 показана історія деформації повзучості цього ламінату для часу релаксації$\tau = 1000$ s Код кроків лінійно в журналі часу, в даному випадку з чотирма часовими кроками на десятиліття. Деформація повзучості - це деформація над початковою пружною деформацією, яка переходить від нуля до того,$C_v \epsilon_{x,0} = 5 \times 10^{-4}$ як час прогресує через час релаксації.

Малюнок 7: Історія деформації повзучості в модельному ламінаті.

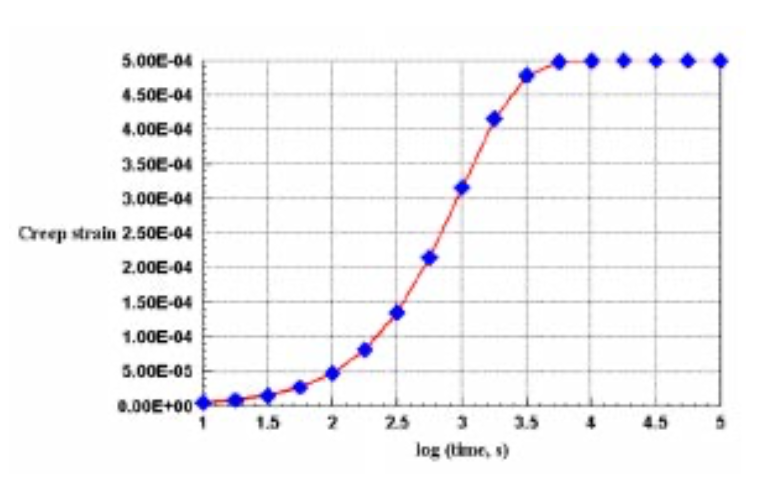
Посилання

1. Ештон, JE, J.C. Halpin і П.Х. Петі, грунтовка з композитних матеріалів: аналіз, Technomic Press, Вестпорт, Коннектикут, 1969.

2. Джонс, Р.М., Механіка композиційних матеріалів, Макгроу-Хілл, Нью-Йорк, 1975.

3. Пауелл, P.C., Інжиніринг з полімерами, Чепмен і Холл, Лондон, 1983.

4. Ройланс, Д., Механіка матеріалів, Wiley & Sons, Нью-Йорк, 1996.

Вправа$\PageIndex{1}$

Випишіть$x-y$ двовимірну матрицю відповідності$\bar{S}$ та матрицю жорсткості$\bar{D}$ (Рівняння 4.4.11) для одного шару графіту/епоксидного композиту з вирівняними по$x-y$ осях волокнами.

Вправа$\PageIndex{2}$

Випишіть$x-y$ двовимірну матрицю відповідності$\bar{S}$ та матрицю жорсткості$\bar{D}$ (Рівняння 4.4.11) для одного шару графіту/епоксидного композиту з вирівняними волокнами 30$^{\circ}$ від$x$ осі.

Вправа$\PageIndex{3}$

Побудуйте ефективний модуль Юнга, виміряний вздовж$x-$ осі, одного односпрямованого шару графіто-епоксидного композиту як функцію кута між напрямком волокна шару та$x-$ віссю.

Вправа$\PageIndex{4}$

Використовуючи мову програмування за вашим вибором, напишіть код ламінату, подібний до коду пластини, згаданого в тексті, і перевірте його, обчисливши жорсткість ламінату і відповідність матриць, наведених у прикладі$\PageIndex{2}$.

Вправа$\PageIndex{5}$

$(60^{\circ}/0^{\circ}/-60^{\circ})^S$Розкладка ($S$верхній індекс вказує, що шари повторюються для отримання симетричного ламінату) є прикладом того, що називаються «квазі-ізотропними» ламінатами, що мають рівні жорсткості в$y$ напрямках$x$ і, незалежно від орієнтації ламінату. Переконайтеся, що це так для двох орієнтацій ламінату, один має 0$^{\circ}$ шарів, орієнтованих вздовж$x$ осі, а інший з 0$^{\circ}$ шарів, орієнтованих на 30$^{\circ}$ від$x$ осі.

Механічні властивості композиційних матеріалів

У наступній таблиці наведено значення фізичних та механічних властивостей для репрезентативних матеріалів шарів та сердечників, широко використовуваних у композитних ламінатах, армованих волокнами. Властивості шару взяті з F.P.Gerstle, «Композити», Енциклопедії полімерних наук та інженерії, Wiley, Нью-Йорк, 1991, з якими слід звернутися до даних з більш широкого спектру матеріалів. Див. також Г.Любін, Довідник з композитів, Ван Ностранд, Нью-Йорк, 1982.

	S-скло/епоксидна смола	Кевлар/епоксидна смола	HM графіт/епоксидна смола	Сосна	Жорсткий пінопласт Rohacell 51
Еластичні властивості: $E_1$, ГПа $E_2$, ГПа $G_{12}$, ГПа $\nu_{12}$	56 16 7,6 0,26	80 5,5 2,1 0,31	230 6,6 4,8 0,25	13,4 0,55 0,83 0,30	0.07 0.07 0,021
Міцність на розрив: $\sigma_1$, МПа $\sigma_2$, МПа $\sigma_{12}$, МПа	1800 40 80	2000 20 40	1100 21 65	78 2,1 6,2	1,9 1,9 0,8
Міцність на стиск: $\sigma_1$, МПа $\sigma_2$, МПа	690 140	280 140	620 170	33 3,0	0,9 0,9
Фізичні властивості: $\alpha_1, 10^{-6}/^{\circ} C$ $\alpha_2, 10^{-6}/^{\circ} C$ Об'ємна частка Товщина,$mm$ Щільність,$Mg/m^3$	2,1 6,3 0,7 0,15 2,0	-4,0 60 0,54 0,13 1,38	-0,7 28 0,7 0,13 1,63	0,55	33 33 0,05