4.2: Напруження в балках

Вступ

Розуміння напружень, викликаних в балках навантаженнями на згинання, зайняло багато років. Галілей працював над цією проблемою, але теорія, якою ми її використовуємо сьогодні, зазвичай приписують головним чином великому математику Леонарду Ейлеру (1707—1783). Як буде розроблено нижче, балки розвивають нормальні напруги в поздовжньому напрямку, які варіюються від максимального натягу на одній поверхні, до нуля на середній площині балки, до максимуму при стисненні на протилежній поверхні. Напруження зсуву також індуковані, хоча вони часто незначні в порівнянні з нормальними напруженнями, коли відношення довжини до висоти балки велике. Процедури розрахунку цих напружень для різних умов навантаження та форм поперечного перерізу балки є, мабуть, найважливішими методами, які можна знайти у вступній механіці матеріалів, і будуть розроблені в наступних розділах. Ця теорія вимагає, щоб користувач міг побудувати діаграми зсувних і згинальних моментів для балки, як розроблено, наприклад, в Модулі 12.

Нормальні стреси

Балка, що піддається позитивному згинальному моменту, буде мати тенденцію до розвитку увігнуто-вгору кривизни. Інтуїтивно це означає, що матеріал біля верхньої частини балки поміщається в стисненні уздовж\(x\) напрямку, при цьому нижня область в напрузі. При переході між областями стиснення і розтягування напруга стає нульовим; це нейтральна вісь балки. Якщо матеріал має тенденцію до невдачі в напрузі, як крейда або скло, він буде робити це шляхом ініціювання тріщин і зростання з нижньої поверхні розтягування. Якщо матеріал сильний на напругу, але слабкий при стисненні, він вийде з ладу на верхній стискаючої поверхні; це може спостерігатися в шматку дерева шляхом стиснення вигин зовнішніх волокон.

Ми шукаємо вираз, що пов'язує величини цих осьових нормальних напружень до зсувного та згинального моменту всередині балки, аналогічно напруженням зсуву, індукованим крученням у круговому валу. По суті, розвиток потрібних відносин слід точно таким же прямим підходом, що і при крутінні:

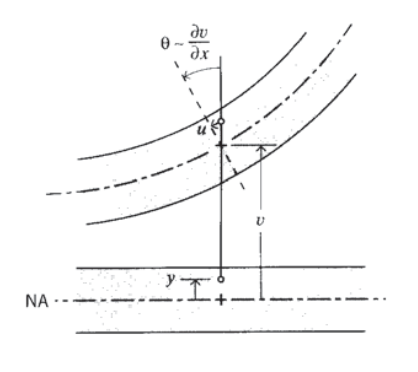
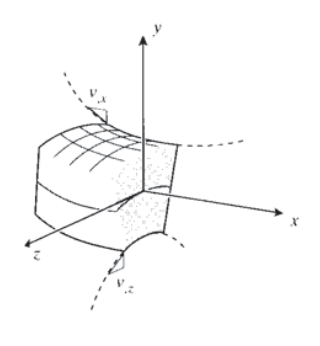
1. Геометричне твердження: Ми починаємо з того, що спочатку поперечні площини всередині балки залишаються площинними під вигином, але обертаються на кут\(\theta\) навколо точок на нейтральній осі, як показано на малюнку 1. Для малих обертань цей кут задається приблизно\(x\) -похідною функції вертикального відхилення променя\(v(x)\) (Точний вираз для кривизни є

\[\dfrac{d \theta}{ds} = \dfrac{d^2 v/dx^2}{[1 + (dv/dx)^2]^{3/2}}.\]

Це дає,\(\theta \approx dv/dx\) коли квадратна похідна в знаменнику мала порівняно з 1. ):

\[u = -y v_{,x}\]

де кома вказує на диференціацію щодо зазначеної змінної (\(v_{,x} \equiv dv/dx\)). Тут\(y\) вимірюється позитивне вгору від нейтральної осі, розташування якої всередині променя ще не визначено.

Малюнок 1: Геометрія вигину балки.

2. Кінематичне рівняння: Нормальна\(\epsilon_x\) деформація\(x\) -напрямок - це градієнт зміщення:

\[\epsilon_x = \dfrac{du}{dx} = -yv_{,xx}\]

Зверніть увагу, що деформації дорівнюють нулю на нейтральній осі\(y = 0\), де, негативні (стискаючі) над віссю, а позитивні (розтягнення) нижче. Вони збільшуються в величині лінійно з\(y\), так само, як деформації зсуву збільшувалися лінійно з\(r\) круговим валом з круговим навантаженням. Величина\(v_{,xx} \equiv d^2v/dx^2\) - це просторова швидкість зміни нахилу кривої прогину балки, «нахил ухилу». Це називається кривизною балки.

3. Установче рівняння: Напруження отримані безпосередньо із закону Гука як

\[\sigma_x = E\epsilon_x = -y Ev_{,xx}\]

Це обмежує застосовність цього похідного до лінійних еластичних матеріалів. Звідси осьове нормальне напруження, як і деформація, зростає лінійно від нуля на нейтральній осі до максимуму на зовнішніх поверхнях балки.

4. Співвідношення рівноваги: Оскільки не існує осьових (\(x\)-напрямних) навантажень, що застосовуються зовні до балки, загальна осьова сила, що створюється нормальними\(\sigma_x\) напруженнями (показана на малюнку 2), повинна дорівнювати нулю. Це може виражатися як

\(\sum F_x = 0 = \int_A \sigma_x dA = \int_A -y Ev_{,xx} dA\)

який вимагає, щоб

\(\int_A y dA = 0\)

Відстань\(\bar{y}\) від нейтральної осі до центроїда площі поперечного перерізу дорівнює

\(\bar{y} = \dfrac{\int_A y dA}{\int_A dA}\)

Отже\(\bar{y} = 0\), тобто нейтральна вісь збігається з центроїдом площі поперечного перерізу балки. Цей результат очевидний при відображенні, так як напруги збільшуються з однаковою лінійною швидкістю, вище осі при стисненні і нижче осі при розтягуванні. Тільки якщо вісь знаходиться точно в центроїдальному положенні, ці напруги будуть балансувати, щоб дати нульову чисту горизонтальну силу і зберегти промінь в горизонтальній рівновазі.

Малюнок 2: Момент і сила рівноваги в балці.

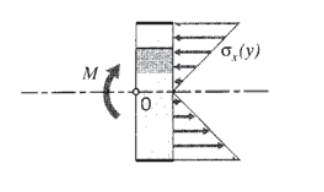
Нормальні напруги при стисненні та розтягуванні врівноважуються, щоб дати нульову чисту горизонтальну силу, але вони також виробляють чистий момент за годинниковою стрілкою. Цей момент повинен дорівнювати значенню\(M(x)\) при цьому значенні\(x\), як видно, приймаючи момент балансу навколо точки\(O\):

\(\sum M_O = 0 = M + \int_A \sigma_x \cdot y dA\)

\[M = \int_A (y Ev_{,xx}) \cdot y dA = Ev_{,xx} \int_A y^2 dA\]

Малюнок 3: Момент інерції для прямокутного перерізу.

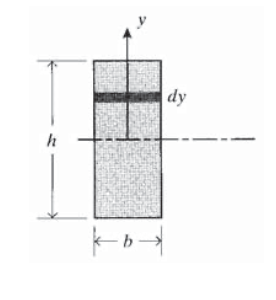
Величина\(\int y^2 dA\) - прямокутний момент інерції щодо центроїдальної осі, що позначається\(I\). Для прямокутного перерізу висоти\(h\) і ширини\(b\), як показано на малюнку 3, це:

\[I = \int_{-h/2}^{h/2} y^2 b dy = \dfrac{bh^3}{12}\]

Розв'язуючи рівняння 4.2.4 для\(v_{,xx}\), кривизна балки дорівнює

\[v_{,xx} = \dfrac{M}{EI}\]

5. Явна формула для напруги може бути отримана, використовуючи це в Рівнянні 4.2.3:

\[\sigma_x = -y E \dfrac{M}{EI} = \dfrac{-My}{I}\]

Остаточний вираз для напруги, Рівняння 4.2.7, схоже\(\tau_{\theta_z} = Tr/J\) на для кручених круглих валів: напруга змінюється лінійно від нуля на нейтральній осі до максимуму на зовнішній поверхні, воно змінюється обернено з моментом інерції поперечного перерізу, і воно не залежить від матеріалу властивості. Подібно до того, як дизайнер надасть перевагу кільцевим приводним валам, щоб максимізувати полярний момент інерції\(J\), балки часто виготовляються з широкими фланцями на верхній та нижній поверхнях для збільшення\(I\).

Приклад\(\PageIndex{1}\): Cantilevered T-beam

Розглянемо консольну таврову балку з розмірами, як показано на малюнку 4, що несе рівномірне навантаження\(w N/m\). Максимальний згинальний момент виникає у стіни, і його легко знайти\(M_{\max} = (wL)(L/2)\). Потім напруга задається рівнянням 4.2.7, що вимагає, щоб ми знали розташування нейтральної осі (оскільки\(y\) і\(I\) вимірюються звідти).

Малюнок 4: Консольна таврова балка.

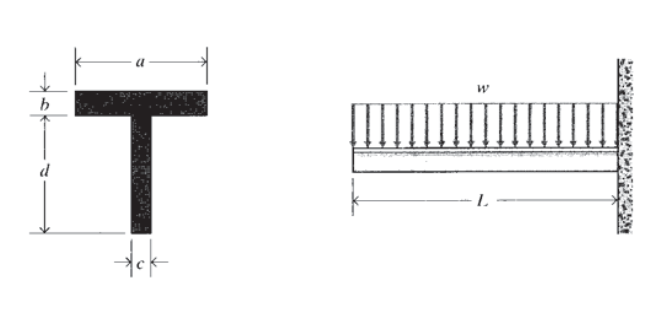
Відстань\(y\) від нижньої частини променя до центроїдальної нейтральної осі можна знайти за допомогою «теореми про композитну площу» (див. Вправа\(\PageIndex{1}\)). Ця теорема стверджує, що відстань від довільної осі до центроїда області, що складається з декількох підрайонів, є сумою підрайонів, що помножуються на відстань до їх окремих центроїдів, розділених на суму підрайонів (тобто загальна площа):

\(\bar{y} = \dfrac{\sum_i A_i \bar{y}_i}{\sum_i A_i}\)

Для нашого прикладу це

\(\bar{y} = \dfrac{(d/2)(cd) + (d + b/2)(ab)}{cd + ab}\)

Моменти інерції окремих частин складеної області по відношенню до власних центроїдів справедливі\(ab^3/12\) і\(cd^3/12\). Ці моменти можна прив'язати до горизонтальної осі через центроїд складеної області за допомогою «теореми паралельної осі» (див. Вправа\(\PageIndex{3}\)). Ця теорема стверджує, що моментом\(I_{z'}\) інерції ділянки\(A\), відносно будь-якої довільної осі,\(z'\) паралельної осі через центроїд, але на відстані\(d\) від нього, є моментом інерції щодо центроїдальної осі\(I_z\) плюс добуток площі\(A\) і квадрат відстані\(d\):

\(I_{z'} = I_z + A d^2\)

Для нашого прикладу це

Моментом інерції всієї площі з'єднання, щодо його центроїда, тоді є сумою цих двох внесків:

\(I = I^{(1)} + I^{(2)}\)

Потім максимальне напруження задається рівнянням 4.2.7, використовуючи це значення\(I\) і\(y = \bar{y}/2\) (відстань від нейтральної осі до зовнішніх волокон) разом з максимальним згинальним моментом\(M_{\max}\). Результатом цих замін є

\(\sigma_x = \dfrac{(3d^2c + 6abd + 3ab^2)wL^2}{2c^2d^4 + 8abcd^3 + 12ab^2cd^2 + 8ab^3cd + 2a^2b^4}\)

На практиці кожен крок, швидше за все, буде зведений до числового значення, а не працювати над алгебраїчним рішенням.

При чистому вигині (застосовуються лише згинальні моменти, відсутні поперечні або поздовжні сили) єдине напруження\(\sigma_x\), задане рівнянням 4.2.7. Всі інші напруги дорівнюють нулю (\(\sigma_y = \sigma_z = \tau_{xy} = \tau_{xz} = \tau_{yz} = 0\)). Однак штами, крім,\(\epsilon_x\) присутні, завдяки ефекту Пуассона. Це не створює деформації зсуву\((\gamma_{xy} = \gamma_{xz} = \gamma_{yz} = 0)\), але нормальні деформації

Штами також можна записати з точки зору викривлень. З рівняння 4.2.2 кривизна вздовж балки дорівнює

\(v_{,xx} = -\dfrac{\epsilon_x}{y}\)

Це супроводжується викривленням, поперечним осі балки, заданої

\(v_{,zz} = -\dfrac{\epsilon_z}{y} = \dfrac{\nu\epsilon_x}{y} = -\nu v_{,xx}\)

Ця поперечна кривизна, показана на малюнку 5, відома як антиеластична кривизна; її можна побачити, зігнувши гумку типу «Рожева перлина» в пальцях.

Малюнок 5: Антиеластична кривизна.

Як і у випадку з конструкціями натягу та кручення, проблеми з вигином часто можна легше вирішити за допомогою енергетичних методів. Знаючи напругу з рівняння 4.2.7, енергію деформації, обумовлену напругою вигину,\(U_b\) можна знайти шляхом інтеграції енергії деформації на одиницю об'єму\(U^* = \sigma^2/2E\) над об'ємом зразка:

\(U_b = \int_V U^* dV = \int_L \int_A \dfrac{\sigma_x^2}{2E} dA dL\)

\(= \int_L \int_A \dfrac{1}{2E} (\dfrac{-My}{I})^2 dA dL = \int_L \dfrac{M^2}{2EI^2} \int_A y^2 dAdL\)

Так як\(\int_A y^2 dA = I\), це стає

\[U_b = \int_L \dfrac{M^2 dL}{2EI}\]

Якщо згинальний момент постійний уздовж балки (однозначно не звичайний випадок), це стає

\(U = \dfrac{M^2 L}{2EI}\)

Це ще один аналог виразу для одновісного натягу,\(U = P^2L/2AE\).

вигин

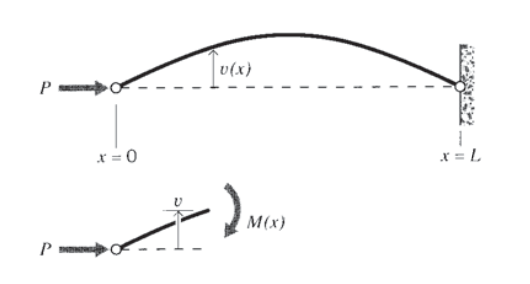
Довгі стрункі колони, поміщені в стиснення, схильні до виходу з ладу при вигині, при якому колона розвиває злам десь по своїй довжині і швидко руйнується, якщо навантаження не розслабляється. Це насправді явище вигину, що рухається згинальним моментом, який розвивається, якщо і коли балка зазнає поперечного прогину. Розглянемо балку, навантажену в осьовому стисненні і закріплену з обох кінців, як показано на малюнку 6. Тепер нехай балка буде зроблена для відхилення поперечно на величину v, можливо, додатковим боковим навантаженням або навіть нерівномірністю в поперечному перерізі балки. Позиції вздовж балки відчують момент, даний

\[M(x) = Pv(x)\]

Власна жорсткість балки буде діяти, щоб відновити прогин і відновити пряму форму, але ефект згинального моменту полягає в тому, щоб відхилити промінь більше. Це битва, над якою виграє вплив. Якщо тенденція згинального моменту до збільшення прогину домінує над здатністю пружної жорсткості балки чинити опір вигину, балка стане нестійкою, продовжуючи згинатися з прискорювальною швидкістю, поки не вийде з ладу.

Малюнок 6: Неминуче вигин в балці.

Згинальний момент пов'язаний з кривизною балки рівнянням 4.2.6, тому поєднання цього з рівнянням 4.2.9 дає

\[v_{,xx} = \dfrac{P}{EI} v\]

Звичайно, це керівне рівняння задовольняється однаково якщо\(v = 0\), тобто промінь прямий. Ми хочемо вийти за рамки цього тривіального рішення і запитати, чи може промінь прийняти зігнуту форму, яка також задовольняла б керівному рівнянню; це означало б, що жорсткість недостатня для відновлення розігнутої форми, так що промінь починає пряжатися. Рівняння 4.2.10 буде задовольнятися функціями, які пропорційні їх власним другим похідним. Тригонометричні функції мають цю властивість, тому рішення кандидатів матимуть вигляд

\(v = c_1 \sin \sqrt{\dfrac{P}{EI}} x + c_2 \cos \sqrt{\dfrac{P}{EI}} x\)

Очевидно, що\(c_2\) повинен бути нулем, так як прогин повинен йти в нуль при\(x = 0\) і\(L\). Далі, синусоїдальний член повинен йти до нуля і в цих двох положеннях, що вимагає,\(L\) щоб довжина була точно дорівнює половині довжини хвилі синусоїдальної функції:

\(\sqrt{\dfrac{P}{EI} L} = n\pi, n = 1, 2, 3, \cdots\)

Найменше значення\(P\) ведучого до деформованої форми відповідає\(n = 1\); критичне навантаження на\(P_{cr}\) вигин тоді:

\[P_{cr} = \dfrac{\pi^2 EI}{L^2}\]

Зверніть увагу на залежність від\(L^2\), тому навантаження на вигин падає з квадратом довжини.

Ця сильна залежність від довжини показує, чому поперечне кріплення так важливо для запобігання вигинається. Якщо дужка додається в середній точці променя, як показано на малюнку 7, щоб усунути там прогин, форма вигину змушена приймати довжину хвилі,\(L\) а не 2\(L\). Це еквівалентно тому, щоб зробити балку вдвічі довшою, що збільшує критичне навантаження на вигин в чотири рази.

Малюнок 7: Вплив бічних опорних та кінцевих умов на вигин балки.

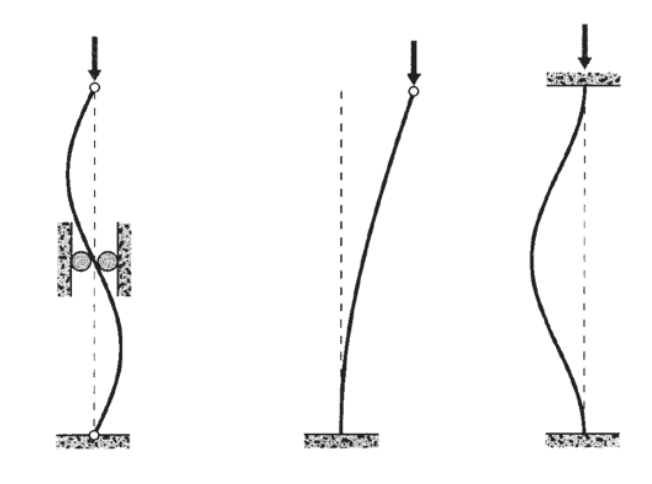
Подібні міркування можуть бути використані для оцінки результату наявності різних умов підтримки. Якщо, наприклад, балка консольна на одному кінці, але не підтримується на іншому, його форма вигин буде чверть синусоїди. Це еквівалентно тому, щоб зробити промінь удвічі довшим, ніж корпус з обома кінцями, тому навантаження на вигин знизиться в чотири рази. Консольні обидва кінці змушують форму повної хвилі, з таким же навантаженням на вигин, як і штифтова балка з опорою середньої точки.

Напруження зсуву

Поперечні навантаження згинають балки, індукуючи осьові розтягуючі і стискаючі нормальні\(x\) деформації в напрямку балки, як обговорювалося вище. Крім того, вони викликають ефекти зсуву, які, як правило, ковзають вертикальні площини дотично один до одного, як показано на малюнку 8, подібно до ковзання гральних карт один за одного. Напруги,\(\tau_{xy}\) пов'язані з цим ефектом зсуву, складають вертикальну силу зсуву, яку ми викликали\(V\), і тепер ми прагнемо зрозуміти, як ці напруги розподіляються по поперечному перерізу балки. Напруження зсуву на вертикальних площинях повинно супроводжуватися рівним напруженням на горизонтальних площинях\(\tau_{xy} = \tau_{yx}\), оскільки, і ці горизонтальні напруги зсуву повинні стати нульовими на верхній і нижній поверхнях балки, якщо там не застосовується тяга для їх збалансування. Значить, вони повинні досягати максимуму десь всередині балки.

Варіацію цього горизонтального напруження зсуву при вертикальному положенні y можна визначити, дослідивши вільне тіло ширини,\(dx\) вирізане з балки на відстань y над нейтральною віссю, як показано на малюнку 9. Момент на лівій вертикальній грані є\(M(x)\), а на правій грані він збільшився до\(M + dM\). Оскільки горизонтальні нормальні напруги прямо пропорційні моменту (\(\sigma x = My/I\)), будь-який приріст моменту дМ на відстані\(dx\) створює дисбаланс горизонтальної сили, що виникає внаслідок нормальних напружень. Цей дисбаланс повинен бути компенсований напругою зсуву\(\tau_{xy}\) на горизонтальній площині при\(y\). Горизонтальний баланс сил записується як

\(\tau_{xy} b dx = \int_{A'} \dfrac{dM \xi}{I} dA'\)

Малюнок 8: Зсувні зсуви при вигині балки.

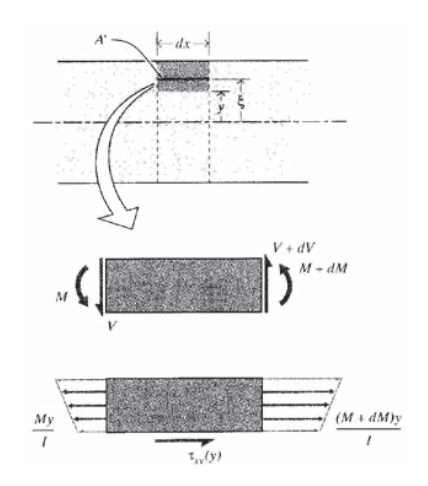
Малюнок 9: Зсувний і згинальний момент в диференційній довжині променя.

де ширина балки при\(b\) -\(y, \xi\) це змінна висота фіктиву, починаючи від\(y\) зовнішньої поверхні балки, і\(A'\) є площею поперечного перерізу між площиною в\(y\) і зовнішньою поверхнею. Використовуючи\(dM = V\ dx\) з Рівняння 4.2.8 модуля 12, це стає

\[\tau_{xy} = \dfrac{V}{Ib} \int_A' \xi dA' = \dfrac{VQ}{Ib}\]

де\(Q(y) = \int_{A'} \xi dA' = \bar{\xi} A'\) ось перший момент області вище\(y\) про нейтральну вісь.

Малюнок 10: Перетин прямокутного бруса.

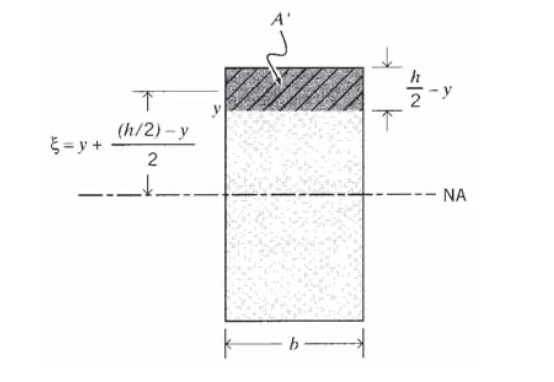
Параметр\(Q(y)\) горезвісний для заплутаних осіб, нових в теорії пучка. Щоб визначити її для заданої висоти\(y\) щодо нейтральної осі, почніть з ескізу поперечного перерізу балки, і проведіть горизонтальну лінію в тому положенні,\(y\) в якому\(Q\) шукається (на рис. 10 показана прямокутна балка постійної ширини\(b\) і висоти\(h\) для ілюстрація). Зверніть увагу на площу\(A'\) між цією лінією і зовнішньою поверхнею (позначено перехресним штрихуванням на малюнку 10). Тепер обчислюємо відстань\(\bar{\xi}\) від нейтральної осі до центроїда\(A'\). Параметр\(Q(y)\) - добуток\(A'\) і\(\xi\); це перший момент площі\(A'\) по відношенню до центроїдальної осі. Для прямокутного бруса він

Зверніть увагу\(Q(y)\), що, а отже,\(\tau_{xy}(y)\) також є параболічним, будучи максимальним на нейтральній осі (\(y\)= 0) і нулем на зовнішній поверхні (\(y = h/2\)). Використовуючи\(I = bh^3/12\) для прямокутної балки, максимальне напруження зсуву, задане рівнянням 4.2.12, становить

\(\tau_{xy, \max} = \tau_{xy}|_{y = 0} = \dfrac{3V}{2bh}\)

(Майте на увазі, ніж два вищевказані вирази для прямокутного перерізу\(Q\) і\(\tau_{xy,\max}\) призначені лише для прямокутного перерізу; перерізи інших фігур матимуть різні результати.) Ці напруження зсуву найбільш важливі в балках, які є короткими щодо їх висоти, оскільки згинальний момент зазвичай збільшується з довжиною, а сила зсуву немає (див. Вправа\(\PageIndex{11}\)). Один стандартний тест на межламінарну міцність на зсув («Очевидна горизонтальна міцність на зсув армованих пластмас методом короткого променя», ASTM D2344, Американське товариство випробувань та матеріалів.) полягає в розміщенні короткого променя на вигин та спостереження за навантаженням, при якому тріщини розвиваються вздовж середньої площини.

Приклад\(\PageIndex{2}\)

Оскільки нормальне напруження є максимальним там, де горизонтальне напруження зсуву дорівнює нулю (у зовнішніх волокон), а напруга зсуву максимальна там, де нормальне напруження дорівнює нулю (на нейтральній осі), часто можна вважати їх по одному. Однак місце з'єднання полотна і фланця в I і T балках часто є місцем особливого інтересу, так як тут обидва напруги можуть приймати істотні значення.

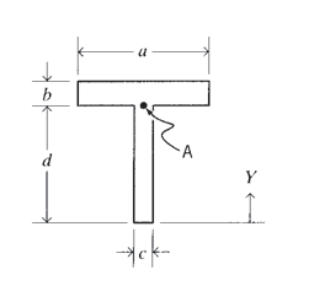
Розглянемо Т-промінь, показаний раніше в прикладі\(\PageIndex{1}\), і вивчіть місце розташування в точці,\(A\) показаній на малюнку 11, в полотні безпосередньо під фланцем. Тут ширина\(b\) в Рівнянні 4.2.12 - це розмірність, позначена\(c\); оскільки промінь тут тонкий, напруга зсуву\(\tau_{xy}\) буде, як правило, велика, але вона різко зменшиться у фланці, коли ширина переходить до більшого значення a. Нормальне напруження в точці\(A\) обчислюється з \(\sigma_x = My/I\), використовуючи\(y = d − y\). Це значення буде майже таким же великим, як напруга зовнішнього волокна, якщо товщина фланця b невелика в порівнянні з висотою полотна\(d\). Коло Мора для напруженого стану в точці\(A\) буде мати помітний внесок від обох\(\sigma_x\) і\(\tau_{xy}\), і може призвести до основного напруження більше, ніж у зовнішніх волокон або нейтральної осі.

Ця проблема дає хороший огляд регулюючих відносин для нормальних і зсувних напружень в балках, а також є природним застосуванням для комп'ютерних методів символічних маніпуляцій. Використовуючи програмне забезпечення Maple, ми можемо почати з обчислення розташування центроїдальної осі:

Малюнок 11: Перетин Т-образної балки.

Тут символом «>» є підказка Maple, а «;» потрібен Maple для завершення команди. Максимальна сила зсуву і згинальний момент (присутній на стіні) визначаються з точки зору розподіленого навантаження і довжини балки як

> ybar := ((d/2)*c*d) + ( (d+(b/2) )*a*b )/( c*d + a*b );  

Для побудови графіків буде зручно мати змінну висоти Y, виміряну знизу секції. Відносини для нормального напруження, напруження зсуву та першого основного напруження є функціями Y; вони визначаються за допомогою команди Maple «procedure»:

> V := w*L;
> M := -(w*L)*(L/2); 

Для побудови графіків буде зручно мати змінну висоти Y, виміряну знизу секції. Відносини для нормального напруження, напруження зсуву та першого основного напруження є функціями Y; вони визначаються за допомогою команди Maple «procedure»:

> sigx := proc (Y) -M*(Y-ybar)/Iz end;
> tauxy := proc (Y) V*Q(Y)/(Iz*B(Y) ) end;
> sigp1 := proc (Y) (sigx(Y)/2) + sqrt( (sigx(Y)/2)^2 + (tauxy(Y))^2 ) end; 

Момент інерції Iz обчислюється як

> I1 := (a*b^3)/12 + a*b* (d+(b/2)-ybar)^2; 
> I2 := (c*d^3)/12 + c*d* ((d/2)-ybar)^2;
> Iz := I1+I2; 

Ширина балки B визначається таким чином, щоб приймати відповідне значення залежно від того, чи є змінна Y в полотні або фланці:

> B:= proc (Y) if Y<d then B:=c else B:=a fi end; 

Команда «fi» («if» пишеться назад) використовується для завершення циклу if-then. Функція Q (Y) визначається для полотна та фланця окремо:

> Q:= proc (Y) if Y<d then
>      int( (yy-ybar)*c,yy=Y..d) + int( (yy-ybar)*a,yy=d..(d+b) )
>    else
>      int( (yy-ybar)*a,yy=Y.. (d+b) ) 
>    fi end;

Тут «int» - це команда Maple для інтеграції, а yy використовується як фіктивна змінна висоти. Чисельні значення різних параметрів визначаються як

> a:=3: b:=1/4: c:=1/4: d:=3-b: L:=8: w:=100: 

Малюнок 12: Напруження на перетині фланцевого з'єднання в короткій консольній Т-балці, що піддаються рівномірному навантаженню.

Нарешті, напруження можна графікувати за допомогою команди Maple plot

> plot({sigx,tauxy,sigp1},Y=0..3,sigx=-500..2500); 

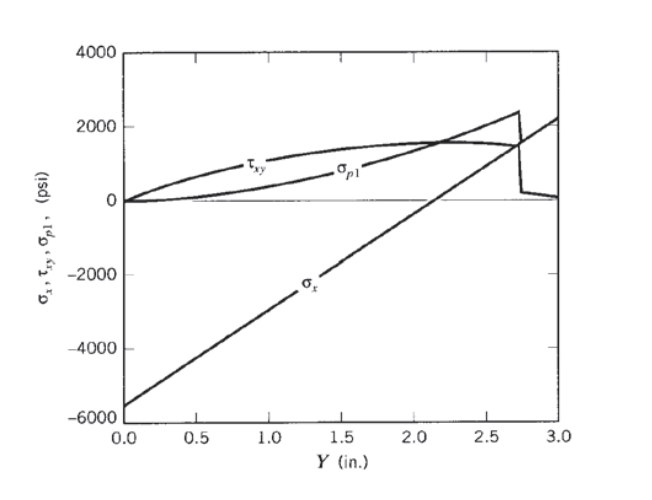
Отриманий графік показаний на малюнку 12.

Приклад\(\PageIndex{3}\)

У попередньому прикладі нас цікавила зміна напруги як функції висоти в балці нерегулярного перерізу. Інша поширена проблема проектування або аналізу полягає в зміні напруги не тільки в залежності від висоти, але і відстані вздовж прольоту розміру балки. Зсувні і згинальні моменти\(M(x)\) змінюються\(V(x)\) і по цьому виміру, і так природно роблять напруги\(\sigma_x (x,y)\) і\(\tau_{xy} (x,y)\) які залежать від них відповідно до рівняння 4.2.7 і 4.2.12.

Малюнок 13: (а) Балка в чотириточковому вигині. (б) Діаграма вільного тіла.

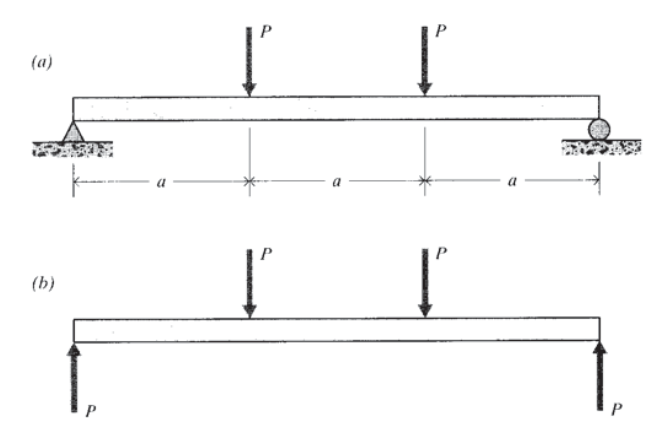
Розглянемо коротку балку прямокутного перерізу, що піддається чотириточковому навантаженню, як показано на малюнку 13. Функції навантаження, зсуву та згинального моменту:

Зсувні і нормальні напруги можуть визначатися як функції цих функцій, так\(x\) і\(y\) безпосередньо з них, а також такі параметри, як основне напруження. Оскільки\(\sigma_y\) нуль скрізь, основна напруга

\(\sigma_{p1} = \dfrac{\sigma_x}{2} + \sqrt{(\dfrac{\sigma_x}{2})^2 + \tau_{xy}^2}\)

Один із способів візуалізації x-y варіації\(\sigma_{p1}\) - це за допомогою 3D-графіка поверхні, який може бути легко підготовлений Maple. Для числових значень\(P = 100, a = h = 10, b = 3\) ми могли б використовувати вирази (відповіді Maple видалені для стислості):

> # use Heaviside for singularity functions
> readlib(Heaviside);
> sfn := proc(x,a,n) (x-a)^n * Heaviside(x-a) end;
> # define shear and bending moment functions
> V:=(x)-> -P*sfn(x,0,0)+P*sfn(x,a,0)+P*sfn(x,2*a,0)-P*sfn(x,3*a,0); 
> M:=(x)-> P*sfn(x,0,1)-P*sfn(x,a,1)-P*sfn(x,2*a,1)+P*sfn(x,3*a,1); 
> # define shear stress function
> tau:=V(x)*Q/(Iz*b);
> Q:=(b/2)*( (h^2/4) -y^2);
> Iz:=b*h^3/12;
> # define normal stress function
> sig:=M(x)*y/Iz;
> # define principal stress
> sigp:= (sig/2) + sqrt( (sig/2)^2 + tau^2 );
> # define numerical parameters
> P:=100;a:=10;h:=10;b:=3;
> # make plot
> plot3d(sigp,x=0..3*a,y=-h/2 .. h/2); 

Отриманий графік показаний на малюнку 14. Домінування параболічного напруження зсуву видно біля кінців балки, оскільки тут сила зсуву знаходиться на максимальному значенні, але згинальний момент невеликий (побудуйте діаграми зсувних і згинальних моментів, щоб підтвердити це). У центральній частині балки, де сила зсуву зникає\(a < x < 2a\), а основне напруження регулюється лише нормальним напруженням\(\sigma_x\), яке лінійно змінюється від нейтральної осі балки. Перше основне напруження дорівнює нулю в стискаючій нижній частині цього перерізу, так як тут\(\sigma_x\) нормальне напруження негативне і правий край кола Мора повинен проходити через нульове значення іншого нормального напруження\(\sigma_y\). Опрацювання графіка на малюнку 14 є хорошим оглядом формул напружень балки.

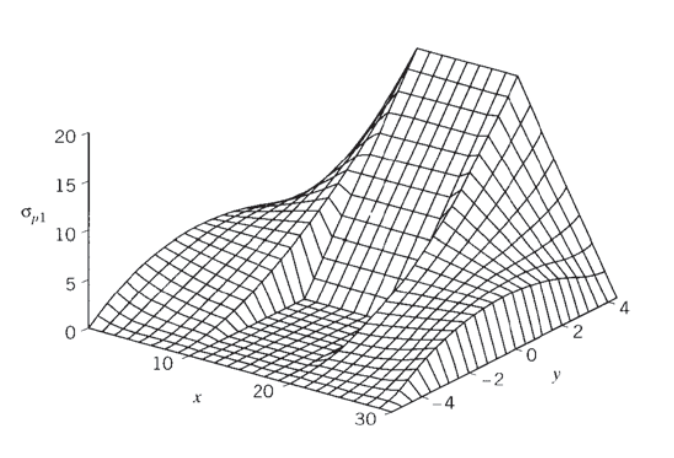
Малюнок 14: Зміна основного напруження при\(\sigma_{p1}\) чотириточковому вигині.

Вправа\(\PageIndex{1}\)

Вивести теорему про композитну площу для визначення центроїда складеної площі.

\(\bar{y} = \dfrac{\sum_i A_i \bar{y}_i}{\sum_i A_i}\)

Вправа\(\PageIndex{2}\)

(a) - (d) Знайдіть центроїди показаних областей.

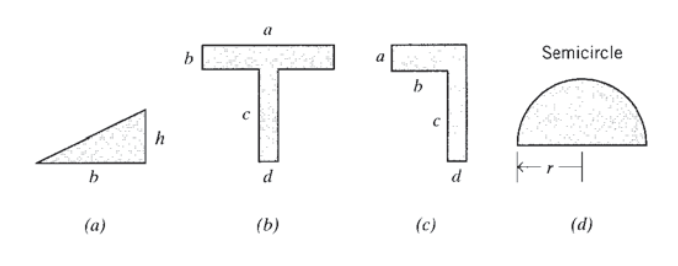
Вправа\(\PageIndex{3}\)

Вивести «теорему паралельної осі» для моментів інерції площини:

\(I_x = I_{xg} + A \bar{y}^2\)

\(I_y = I_{yg} + A \bar{x}^2\)

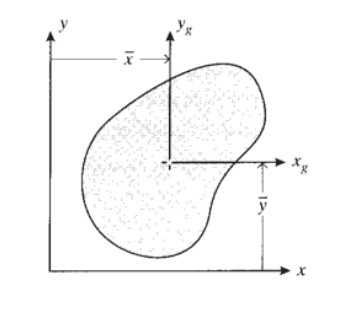
Вправа\(\PageIndex{4}\)

(а) - (d) Визначити момент інерції щодо горизонтальної центроїдальної осі показаних областей.

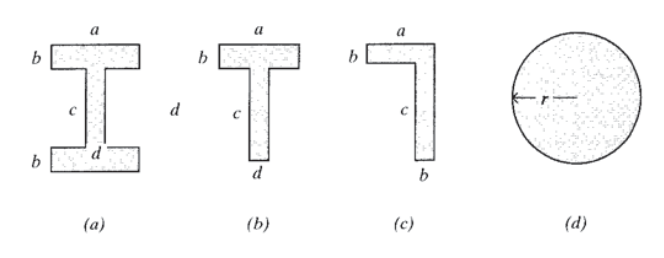
Вправа\(\PageIndex{5}\)

Покажіть, що момент інерції перетворюється щодо обертань осі точно так само, як і напруга:

де\(I_x\) і\(I_y\) - моменти інерції щодо\(y\) осей\(x\) і відповідно і\(I_{xy}\) є добутком інерції, що визначається як

\(I_{xy} = \int_A xy dA\)

Вправа\(\PageIndex{6}\)

(a) — (h) Визначте максимальне нормальне напруження σ x у зображених тут балках, використовуючи значення (за потребою)\(L = 25\ in\)\(a = 5 \ in\),\(w = 10\ lb/in\),\(P = 150\ lb\). Припустимо прямокутне перетин шириною\(b = 1\) в і висотою\(h = 2\ in\).

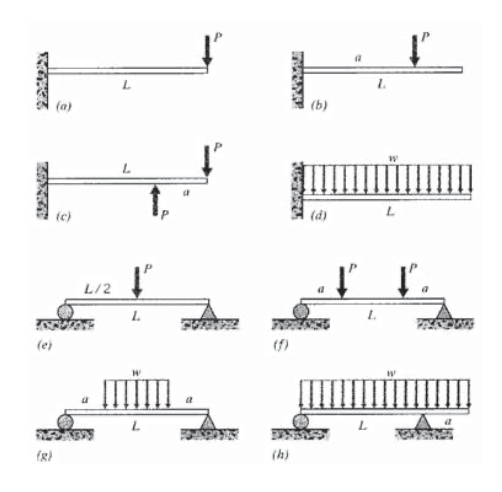
Вправа\(\PageIndex{7}\)

Обґрунтувати твердження в тесті ASTM D790, «Стандартні методи випробувань на згинальні властивості неармованих і армованих пластмас і електроізоляційних матеріалів», який говорить:

Коли балка з однорідного, еластичного матеріалу випробовується на вигин як проста балка, підтримувана в двох точках і навантажена в середній точці, максимальне напруження в зовнішніх волокні виникає в середині прольоту. Це напруження може бути розраховане для будь-якої точки на кривій відхилення навантаження за наступним рівнянням:

\(S = 3PL/2bd^2\)

де\(S\) = напруга в зовнішніх волокні на середині прольоту, МПа;\(P\) = навантаження в заданій точці на кривій відхилення навантаження;\(L\) = проліт опори, мм;\(b\) = ширина досліджуваної балки, мм; і d = глибина досліджуваної балки, мм.

Вправа\(\PageIndex{8}\)

Обґрунтувати твердження в тесті ASTM D790, «Стандартні методи випробувань на згинальні властивості неармованих і армованих пластмас і електроізоляційних матеріалів», який говорить:

Дотичний модуль пружності, який часто називають «модулем пружності», - це відношення, в межах межі пружності напруги до відповідної деформації і повинно виражатися в мегапаскалах. Він обчислюється шляхом малювання дотичної до найкрутішої початкової прямолінійної частини кривої відхилення навантаження та використання [вираз:]

\(E_b = L^3 m/4bd^3\)

де\(E_b\) = модуль пружності при вигині, МПа;\(L\) = опорний проліт, мм;\(d\) = глибина досліджуваної балки, мм; і\(m\) = нахил дотичної до початкової прямолінійної частини кривої відхилення навантаження,\(N/mm\) прогину.

Вправа\(\PageIndex{9}\)

Прямокутний брус повинен бути фрезерований з круглого штока, як показано на малюнку. Яким має бути відношення висоти до ширини,\((b/h)\) щоб мінімізувати напруження при введенні балки на вигин?

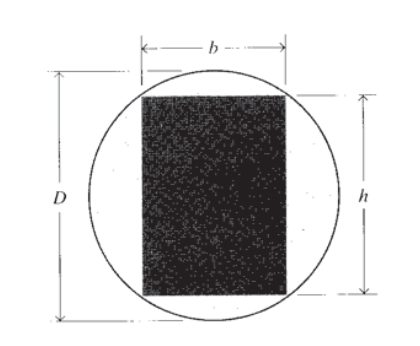
Вправа\(\PageIndex{10}\)

(a) - (h) Визначте максимальний зсув δxy в пучках вправи\(\PageIndex{6}\), використовуючи значення (за потребою)\(L = 25\ in, a = 5\ in, w = 10\ lb/in, P = 150\ lb\). Припустимо прямокутне перетин шириною\(b = 1\) в і висотою\(h = 2\ in\).

Вправа\(\PageIndex{11}\)

Показати, що відношення максимального напруження зсуву до максимального нормального напруження в балці, що піддається 3-точковому вигину, становить

\(\dfrac{\tau}{\sigma} = \dfrac{h}{2L}\)

Звідси важливість напруги зсуву збільшується, оскільки балка стає коротшою в порівнянні з її висотою.

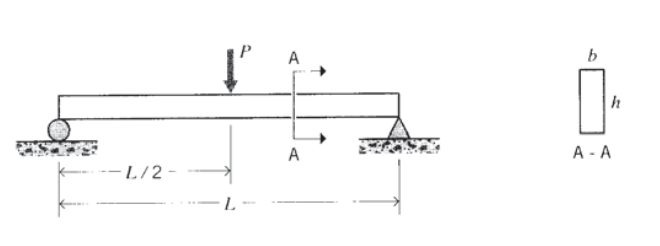
Вправа\(\PageIndex{12}\)

Прочитайте тест ASTM D4475, «Стандартний метод випробувань для видимої горизонтальної міцності на зсув пултрузійних армованих пластикових стрижнів методом короткого променя» і обґрунтуйте вираз, наведений там для видимої міцності на зсув:

\(S = 0.849 P/d^2\)

де\(S\) = видима міцність на зсув\(N/m^2\),, (або psi);\(P\) = розривне навантаження\(N\),, (або lbf); і\(d\) = діаметр зразка, м (або дюйм.).

Вправа\(\PageIndex{13}\)

Для Т-балки, показаної тут, з розмірами\(L = 3, a = 0.05, b = 0.005, c = 0.005, d = 0.7\) (все в\(m\)) та розподілом навантаження\(w = 5000 N/m\), визначте основне та максимальне напруження зсуву в точці\(A\).

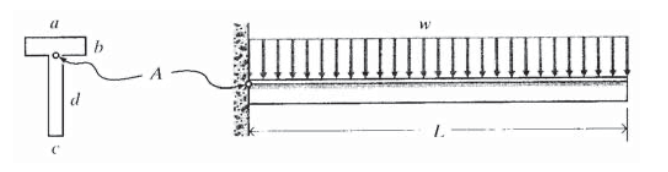
Вправа\(\PageIndex{14}\)

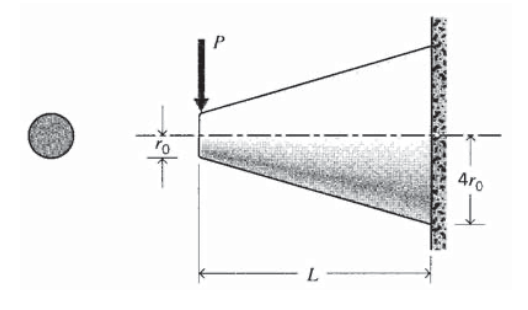
Визначте максимальне нормальне напруження в консольній балці круглого перерізу, радіус якої лінійно змінюється від\(4r_0\) до\(r_0\) відстані\(L\), навантаженої з силою\(P\) на вільному кінці.

Вправа\(\PageIndex{15}\)

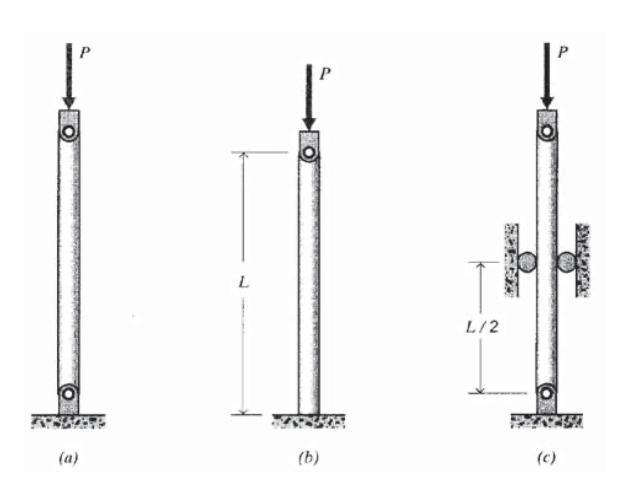
Колона з вуглецевої сталі має довжину\(L = 1\ m\) і круглий перетин діаметра\(d = 20\ mm\). Визначте критичне навантаження\(P_c\) на вигин для випадку (а) обидва кінці закріплені, (b) один кінець консольно, (c) обидва кінці закріплені, але підтримуються збоку в середній точці.

Вправа\(\PageIndex{16}\)

Колона з вуглецевої сталі має довжину\(L = 1\ m\) і круглий перетин. Визначте діаметр,\(d\) при якому колона має рівну ймовірність вигину або поступливості при стисненні.