4.3: Зсуви променя
- Page ID
- 30697
Вступ
Ми хочемо бути в змозі передбачити прогин балок при згинанні, тому що багато додатків мають обмеження на величину прогину, яку можна допустити. Інша поширена потреба в аналізі прогину виникає при випробуванні матеріалів, при якому вимірюється поперечний прогин, викликаний навантаженням на вигин. Якщо ми знаємо очікуване співвідношення між навантаженням та відхиленням, ми можемо «відступити» властивості матеріалу (зокрема модуль) від вимірювання. Ми покажемо, наприклад, що прогин в середній точці балки, що піддається «триточковому вигину» (балка, навантажена в її центрі і просто підтримується на її краях) є
\(\delta_P = \dfrac{PL^3}{48EI}\)
де довжина\(L\) і момент інерції\(I\) - геометричні параметри. Якщо відношення\(\delta_P\) до\(P\) вимірюється експериментальним шляхом, модуль\(E\) можна визначити. Жорсткість, виміряна таким чином, називається модулем вигину.
Існує ряд підходів до проблеми прогину променя, і багато текстів витрачають багато друку на цю тему. Наступне лікування описує лише деякі з більш простих методів, більше з метою розуміння загальних понять, ніж з розробкою великої кількості засобів для їх виконання вручну. На практиці інженери-конструктори зазвичай консультуються з таблицями довідників формул відхилення за потребою, тому ще до комп'ютерного віку багато з цих методів були трохи академічними.
Багаторазова інтеграція
У модулі 12 ми побачили, як дві інтеграції функції навантаження\(q(x)\) виробляють спочатку функцію зсуву,\(V(x)\) а потім функцію моменту\(M(x)\):
\[V = - \int q(x) dx + c_1\]
\[M = - \int V(x) dx + c_2\]
де константи інтеграції\(c_1\) і\(c_2\) оцінюються з відповідних граничних умов на\(V\) і\(M\). (Якщо використовуються функції сингулярності, граничні умови включаються явно і константи інтеграції\(c_1\) і\(c_2\) однаково нульові.) З Рівняння 6 у модулі 13 кривизна\(v_{,xx} (x)\) - це лише момент, розділений на модуль перетину\(EI\). Ще дві інтеграції потім дають
\[v_{,x} (x) = \dfrac{1}{EI} \int M(x) dx + c_3\]
\[v(x) = \int v_{,x} (x) + c_4\]
де\(c_3\) і\(c_4\) визначаються з граничних умов на схилі або прогині.
Приклад\(\PageIndex{1}\)
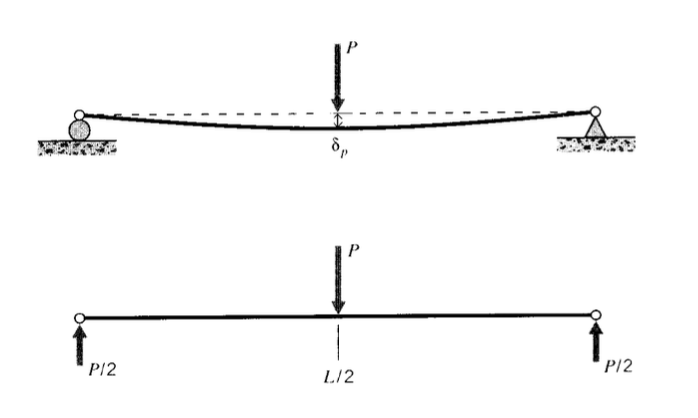
Як ілюстрацію цього процесу розглянемо випадок «триточкового вигину», показаний на малюнку 1. Ця геометрія часто використовується при випробуванні матеріалів, оскільки дозволяє уникнути необхідності затискати зразок до випробувального апарату. Якщо навантаження\(P\) прикладається в середній точці, сили реакції при\(A\) і\(B\) дорівнюють половині прикладеного навантаження. Потім функція завантаження
Інтеграція за вищевказаною схемою:
\[\begin{array} {c} {V(x) = - \dfrac{P}{2} \langle x \rangle^0 + P \langle x - \dfrac{L}{2} \rangle^0} \\ {M(x) = \dfrac{P}{2} \langle x \rangle^1 - P \langle x - \dfrac{L}{2} \rangle^1} \\ {EIv_{,x} (x) = \dfrac{P}{4} \langle x \rangle^2 - \dfrac{P}{2} \langle x - \dfrac{L}{2} \rangle^2 + c_3} \end{array}\]
Від симетрії балка має нульовий ухил в середній точці. Отже\(v_{,x} = 0 @ x = L/2\), так\(c_3\) можна знайти, щоб бути\(-PL^2/16\). Інтеграція знову:
Прогин дорівнює нулю на лівому кінці, так що\(c_4 = 0\). Переставляючи, прогин балки задається шляхом
\[v = \dfrac{P}{48EI} [4x^3 - 3L^2x - 8 \langle x - \dfrac{L}{2} \rangle^3]\]
Максимальний прогин відбувається при\(x = L/2\), який ми можемо оцінити безпосередньо перед терміном сингулярності
\[\delta_{\max} = \dfrac{PL^3}{48EI}\]
Цей вираз широко використовується при випробуванні на вигин, і є прикладом, який використовується для початку цього модуля.
Перш ніж\(q(x)\) можна буде записати функцію навантаження, необхідно визначити сили реакції на опорах балки. Якщо промінь статично детермінантний, як у наведеному вище прикладі, це можна зробити, викликавши рівняння статичної рівноваги. Статична детермінантність означає, що можуть бути присутніми лише дві сили реакції або моменти, оскільки ми маємо лише баланс сил у напрямку, поперечному осі променя, і одне рівняння моменту. Прикладами таких визначених балок є просто спирається балка (одна спирається тільки на дві опори) або просто консольна балка; в першому випадку на кожній опорі припадає одна сила реакції, а в останньому - одна поперечна сила і один момент на затиснутому кінці.
Звичайно, немає жорстких інженерних підстав обмежувати кількість опор балок достатніми для статичної рівноваги. Додавання «зайвих» опор обмежить деформації і напруги, і це часто буде варто, незважаючи на додаткові витрати на будівництво. Але аналіз зараз трохи складніше, так як не всі невідомі реакції можна знайти з рівнянь статичної рівноваги. У цих статично невизначених випадках необхідно буде викликати геометричні обмеження, щоб розробити достатню кількість рівнянь для вирішення проблеми.
Це робиться шляхом написання рівнянь нахилу і відхилення, несучи невідомі сили реакції і моменти як невизначені параметри. Потім укоси і прогини встановлюються на їх відомі значення на опорах, а отримані рівняння вирішуються для невідомих. Якщо, наприклад, балка спирається на три опори, буде три невідомі сили реакції, і нам знадобиться загалом п'ять рівнянь: три для невідомих сил і ще два для констант інтеграції, що виникають при написанні рівнянь нахилу та відхилення. Два з цих рівнянь задаються статичною рівновагою, а ще три виходять установкою прогинів у опор на нуль. Наступний приклад ілюструє процедуру, яка проста, хоча і виснажлива, якщо зробити це вручну.
Приклад\(\PageIndex{2}\)
Розглянемо потрійну опорну балку довжини,\(L = 15\) як показано на малюнку 2, що несе постійну рівномірну навантаження\(w = -10\). Не існує достатніх рівнянь рівноваги для визначення сил реакції\(R_a\)\(R_b\), і\(R_c\), тому вони залишаються невідомими, тоді як багаторазове інтегрування використовується для розробки рівняння відхилення:
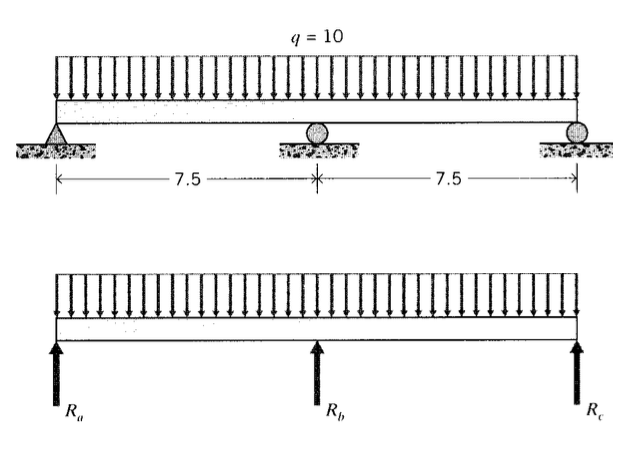
Ці рівняння мають 5 невідомих:\(R_a, R_b, R_c, c_1\), і\(c_2\). Вони повинні бути отримані з двох рівнянь рівноваги
і три відомих нульових зміщення на опорах
\(y(0) = y(L/2) = y(L) = 0\)
Хоча процес простий, є багато алгебри, щоб пробратися. Статично невизначені промені, як правило, генерують нудну математику, але, на щастя, це може бути значно зменшено сучасним програмним забезпеченням. Дотримуйтесь того, як легко цей приклад обробляється пакунком Maple V (деякі відповіді Maple видалені для стислості):
> # read the library containing the Heaviside function
> readlib(Heaviside);
> # use the Heaviside function to define singularity functions;
> # sfn(x,a,n) is same is <x-a>^n
> sfn := proc(x,a,n) (x-a)^n * Heaviside(x-a) end;
> # define the deflection function:
> y := (x)-> (Ra/6)*sfn(x,0,3)+(Rb/6)*sfn(x,7.5,3)+(Rc/6)*sfn(x,15,3)
> -(10/24)*sfn(x,0,4)+c1*x+c2;
> # Now define the five constraint equations; first vertical equilibrium:
> eq1 := 0=Ra+Rb+Rc-(10*15);
> # rotational equilibrium:
> eq2 := 0=(10*15*7.5)-Rb*7.5-Rc*15;
> # Now the three zero displacements at the supports:
> eq3 := y(0)=0;
> eq4 := y(7.5)=0;
> eq5 := y(15)=0;
> # set precision; 4 digits is enough:
> Digits:=4;
> # solve the 5 equations for the 5 unknowns:
> solve({eq1,eq2,eq3,eq4,eq5},{Ra,Rb,Rc,c1,c2});
{c2 = 0, c1 = -87.82, Rb = 93.78, Ra = 28.11, Rc = 28.11}
> # assign the known values for plotting purposes:
> c1:=-87.82;c2:=0;Ra:=28.11;Rb:=93.78;Rc:=28.11;
> # the equation of the deflection curve is:
> y(x);
3 3
4.686 x Heaviside(x) + 15.63 (x - 7.5) Heaviside(x - 7.5)
3 4
+ 4.686 (x - 15) Heaviside(x - 15) - 5/12 x Heaviside(x) - 87.82 x
> # plot the deflection curve:
> plot(y(x),x=0..15);
> # The maximum deflection occurs at the quarter points:
> y(15/4);
-164.7
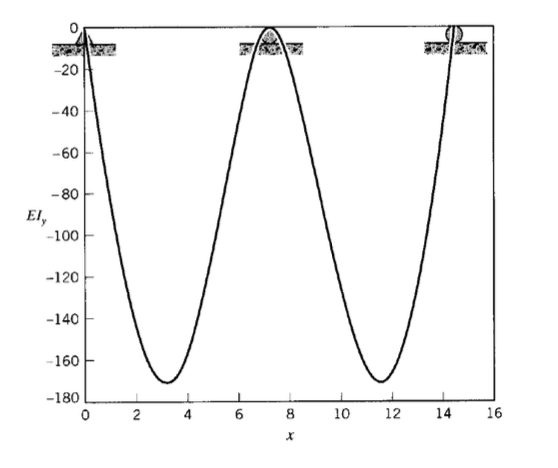
Графік кривої відхилення показаний на малюнку 3.
Енергетичний метод
Енергія деформації при згинанні, задана рівнянням 8 модуля 13, може бути використана для пошуку прогинів, і це може бути зручнішим, ніж послідовне об'єднання, якщо бажаний прогин лише в одній точці. Теорема Кастільяно дає конгруентний відхилення навантаженню\(P\) як
\(\delta_P = \dfrac{\partial U}{\partial P} = \dfrac{\partial}{\partial P} \int_L \dfrac{M^2 dx}{2EI}\)
Зазвичай зручніше робити диференціацію перед інтеграцією, оскільки це знижує порядок виразу в integrand:
\(\delta P = \int_L \dfrac{M}{EI} \dfrac{\partial M}{\partial P} dx\)
де тут\(E\) і\(I\) передбачається не варіюватися с\(x\).
Зсувний внесок у згинання можна отримати аналогічним чином. Знаючи напругу зсуву\(\tau = VQ/Ib\) (опускаючи\(xy\) індекс\(\tau\) на даний момент),\(U_s\) можна записати енергію деформації внаслідок зсуву
\(U_s = \int_V \dfrac{\tau^2}{2G} dV = \int_L \dfrac{V^2}{2GI} \left [\int_A \dfrac{Q^2}{L^2} dA \right ] dx\)
Інтеграл над площею поперечного перерізу\(A\) є чисто геометричним фактором, і ми можемо записати
\[U_s = \int_L \dfrac{V^2 f_s}{2GA} dA \]
де\(f_s\) є безрозмірним форм-фактором для зсуву, визначеного як
\[f_s = \dfrac{A}{I^2} \int_A \dfrac{Q^2}{b^2} dA\]
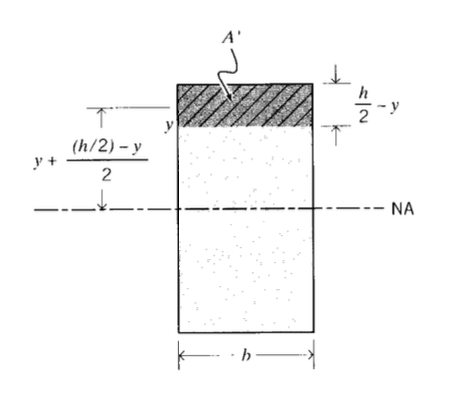
Оцінюючи\(f_s\) прямокутні перерізи для ілюстрації (див. Рис. 4), ми маємо в такому випадку
\(A = bh, I = \dfrac{bh^3}{12}\)
\(f_s = \dfrac{(bh)}{(bh^3/12)^2} \int_{-h/2}^{h/2} \dfrac{1}{b^2} Q dy = \dfrac{6}{5}\)
Звідси\(f_s\) однаковий для всіх прямокутних перетинів, незалежно від їх конкретних розмірів. Аналогічно можна показати (див. Вправа\(\PageIndex{3}\)), що для суцільних круглих перетинів\(f_s\) = 10/9 і для порожнистих круглих секцій\(f_s\) = 2.
Приклад\(\PageIndex{3}\)
Якщо, наприклад, ми шукаємо відхилення під навантаженням\(P\) у триточковому прикладі вигину, зробленому раніше, ми можемо диференціювати момент, заданий у рівнянні 4.3.5, щоб отримати
Тоді
Розширення цього та коригування меж інтеграції з урахуванням функцій особливості, які не були активовані:
\(= -\dfrac{PL^3}{48EI}\)
як і раніше.
Внесок зсуву в відхилення можна знайти, використовуючи\(V = P/2\) в рівнянні енергії деформації. Для випадку прямокутного бруса з у\(f_s = 6/5\) нас є:
\(U_s = \dfrac{(P/2)^2 (6/5)}{2GA}L\)
\(\delta_{P,s} = \dfrac{\partial U_s}{\partial P} = \dfrac{6PL}{20GA}\)
Внесок зсуву можна порівняти з внеском згинання, замінивши на\(12I/h^2\) (\(A\)з\(A = bh\) і\(I = bh^3/12\)). Тоді відношення зсуву до згинальних внесків становить
\(\dfrac{PLh^2/40GI}{PL^3/24EI} = \dfrac{3h^2 E}{5L^2G}\)
Звідси важливість терміну зсуву масштабується як (h/l) 2, тобто квадратично як відношення проміжку до глибини.
Енергетичний метод часто зручний для систем, що мають складну геометрію і комбінговане навантаження. Для тонких валів, що передають осьові, крутильні, згинальні та зсувні навантаження, енергія деформації
\[U = \int_L \left (\dfrac{P^2}{2EA} + \dfrac{T^2}{2GJ} + \dfrac{M^2}{2EI} + \dfrac{V^2f_s}{2GA} \right ) dx\]
Приклад\(\PageIndex{4}\)
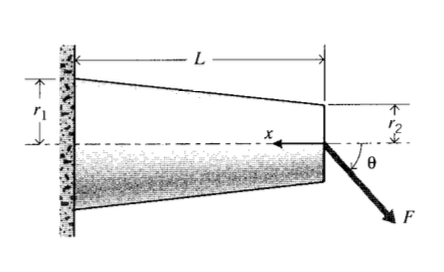
Розглянемо консольну кругову балку, як показано на малюнку 5, яка звужується від радіуса\(r_1\) до\(r_2\) довжини\(L\). Бажаємо визначити прогин, викликаний силою,\(F\) прикладеною до вільного кінця балки, під кутом\(\theta\) від горизонталі. Звертаючись до Maple, щоб уникнути алгебраїчного нудьга, розмірні параметри, необхідні в рівнянні 4.3.10, визначаються як:
> r := proc (x) r1 + (r2-r1)*(x/L) end; > A := proc (r) Pi*(r(x))^2 end; > Iz := proc (r) Pi*(r(x))^4 /4 end; > Jp := proc (r) Pi*(r(x))^4 /2 end;
де r (x) - радіус, A (r) - площа перерізу, Iz - прямокутний момент інерції, а Jp - полярний момент інерції. Осьові, згинальні та зсувні навантаження наведені в терміні\(F\) як
> P := F* cos(theta); > V := F* sin(theta); > M := proc (x) -F* sin(theta) * x end;
Енергії деформації, що відповідають натягу, вигину та зсуву, є
> U1 := P^2/(2*E*A(r)); > U2 := (M(x))^2/(2*E*Iz(r)); > U3 := V^2*(10/9)/(2*G*A(r)); > U := int( U1+U2+U3, x=0..L);
Нарешті, відхилення, конгруентне навантаженню,\(F\) отримують шляхом диференціації загальної енергії деформації:
> dF := diff(U,F);
Результат цих маніпуляцій дає
Це зміщення відбувається в напрямку\(F\) прикладеної сили; горизонтальні і вертикальні прогини кінця балки потім
\(\delta_x = \delta_F \cos \theta\)
\(\delta_y = \delta_F \sin \theta\)
суперпозиція
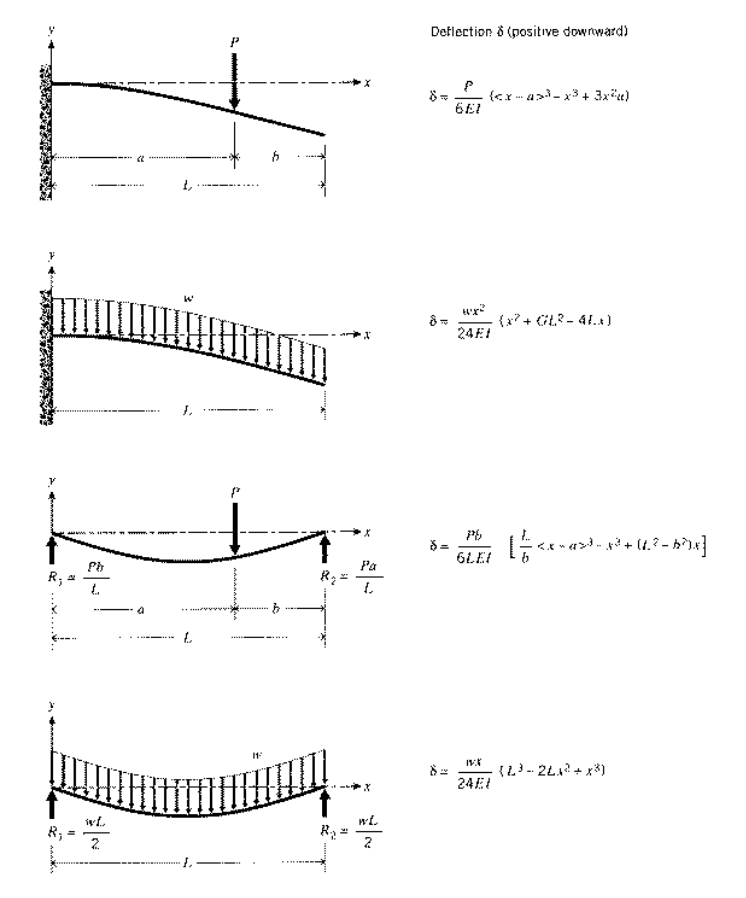
На практиці багато балок будуть навантажуватися складним чином, що складається з декількох зосереджених або розподілених навантажень, що діють в різних місцях уздовж балки. Хоча ці випадки з кількома навантаженнями можуть бути вирішені з нуля, використовуючи описані вище методи, часто простіше вирішити проблему шляхом накладання рішень більш простих завдань, рішення яких наведені в таблицю. На малюнку 6 наведено скорочену колекцію формул відхилення (Більш вичерпний перелік доступний у W.C. Young, Формули Roark для стресу та деформації, McGraw-Hill, Нью-Йорк, 1989.), яких вистачить для багатьох проблем. Підхід суперпозиції є дійсним, оскільки керівні рівняння є лінійними; отже, реакція на комбінацію навантажень - це сума відповідей, які будуть генеруватися кожним окремим навантаженням, що діє окремо.
Приклад\(\PageIndex{5}\)
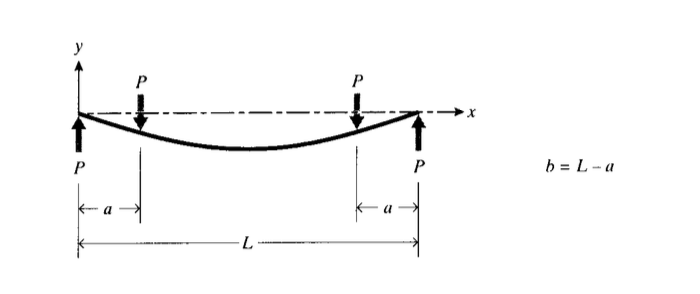
Ми хочемо знайти рівняння кривої відхилення для променевої балки, завантаженої симетричним чотириточковим вигином, як показано на малюнку 7. З малюнка 6 прогин балки з одним навантаженням на відстані\(a\) від лівого кінця дорівнює\(\delta (x) = \dfrac{Pb}{6LEI} [\dfrac{L}{b} \langle x - a \rangle^3 - x^3 + (L^2 - b^2) x]\). Наша теперішня проблема полягає лише в двох таких навантаженнях, що діють одночасно, тому ми маємо
У деяких випадках проектувальнику може не знадобитися вся крива відхилення, і накладання табличних результатів для максимального відхилення та нахилу однаково справедливо.
Вправа\(\PageIndex{1}\)
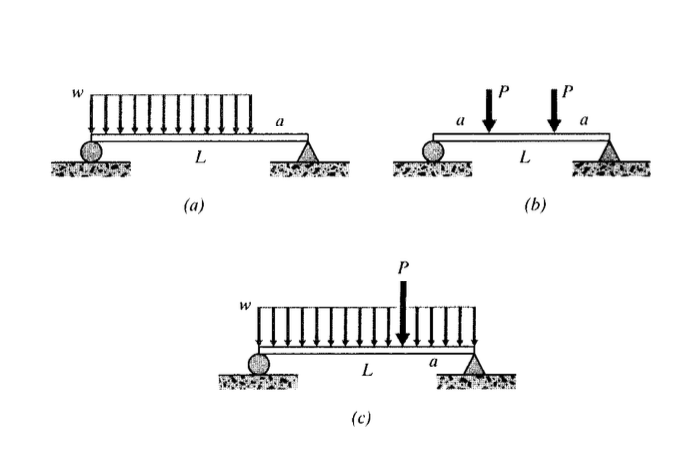
(a) - (h) Запишіть вирази для кривих нахилу та відхилення балок, показаних тут.
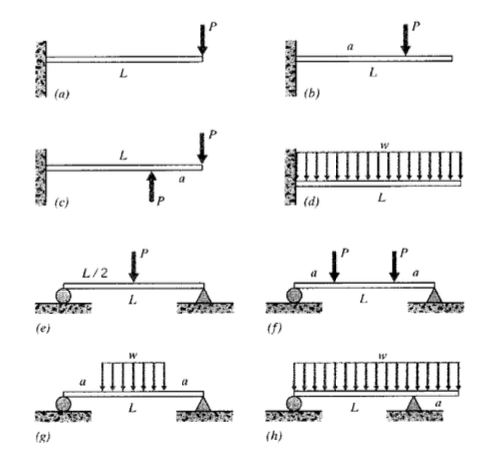
Вправа\(\PageIndex{2}\)
(a) - (h) Використовуйте програмне забезпечення MapLeV (або інше) для побудови кривих нахилу та відхилення для балок у Вправі\(\PageIndex{1}\), використовуючи значення (за потребою)\(L = 25\ in, a = 15\ in, w = 10\ lb/in, P = 150\ lb\).
Вправа\(\PageIndex{3}\)
Показати, що коефіцієнт форми для зсуву для круглого перерізу дорівнює
\(f_s = \dfrac{A}{I^2} \int_A \dfrac{Q}{b^2} dA = \dfrac{10}{9}\)
Вправа\(\PageIndex{4}\)
(a) - (b) Визначте криві відхилення для балок, показаних тут. Побудуйте ці криві для значень (за потребою)\(L = 25\ in, a = 5\ in, w = 10\ lb/in, P = 150\ lb\).
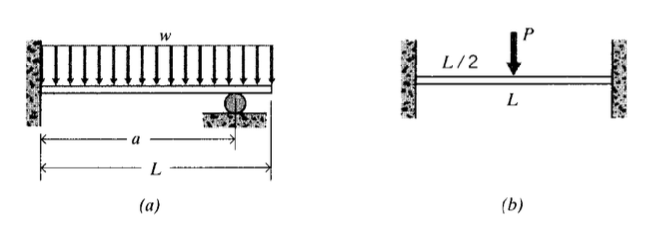
Вправа\(\PageIndex{5}\)
(а) Визначте відхилення пружини котушки під впливом осьової сили\(F\), включаючи внесок ефектів згинання, прямого зсуву та крутильного зсуву. Використовуючи\(r = 1\ mm\) і\(R = 10\ mm\), обчислити відносні величини трьох внесків.
(b) Повторіть розчин в (а), але візьміть осьове навантаження, яке буде розміщено на зовнішньому радіусі котушки.
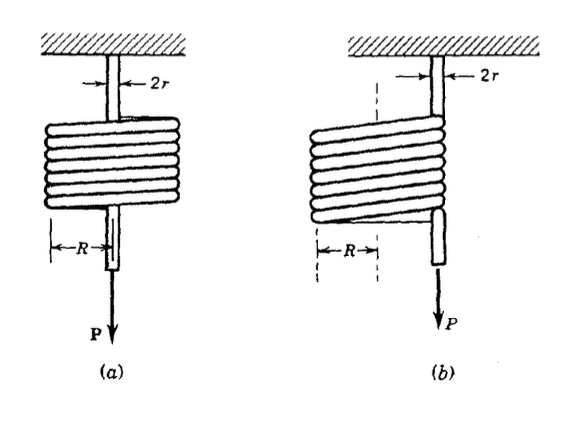
Вправа\(\PageIndex{6}\)
(a) - (c) Використовуйте метод суперпозиції для написання виразів для кривої відхилення\(\delta (x)\) для випадків, показаних тут.