4.1: Діаграми зсуву та згинального моменту
- Page ID
- 30690
Вступ
Балки являють собою довгі і стрункі конструктивні елементи, що відрізняються від кроквяних елементів тим, що покликані підтримувати як поперечні, так і осьові навантаження. Місця їх кріплення також можуть бути більш складними, ніж у кроквяних елементів: вони можуть бути з'єднані болтами або звареними між собою, тому кріплення можуть передавати згинальні моменти або поперечні зусилля в балку. Балки є одними з найпоширеніших з усіх конструктивних елементів, будучи несучими рамами літаків, будівель, автомобілів, людей і багато іншого.
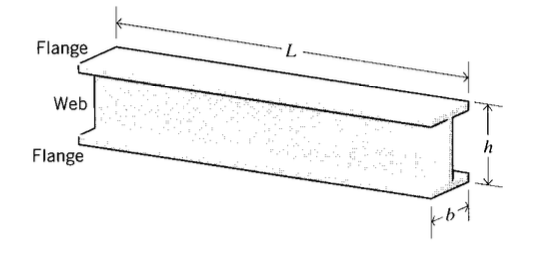
Номенклатура балок досить стандартна: як показано на малюнку 1,\(L\) це довжина, або проліт;\(b\) є шириною, і\(h\) є висотою (також називається глибиною). Форма поперечного перерізу не повинна бути прямокутною, і часто складається з вертикального полотна, що розділяє горизонтальні фланці у верхній і нижній частині балки (Існує стандартизований протокол для позначення конструкційних сталевих балок; наприклад, W 8 × 40 вказує на широкофланцеву балку з номінальною глибиною 8 ′ і вагою 40 фунтів/фут довжини)
Як буде видно в модулі 13 і 14, напруги і прогини, індуковані в балці при навантаженнях на вигин, змінюються по довжині і висоті балки. Перший крок розрахунку цих величин та їх просторової зміни полягає у побудові діаграм зсувного та згинального моменту,\(V(x)\) а також\(M(x)\), які є внутрішніми зусиллями зсуву та згинальними моментами, індукованими в балці, побудованими по довжині балки. У наступних розділах буде описано, як робляться ці схеми.
Діаграми вільного тіла
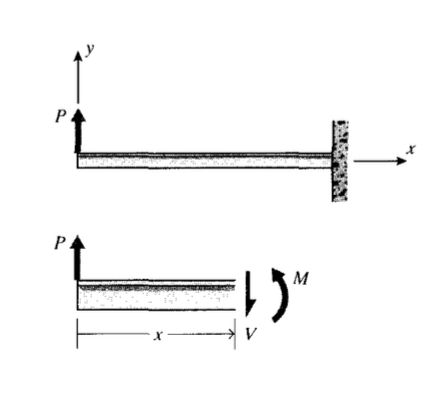
Як простий стартовий приклад розглянемо балку, затиснуту (\ консольно») на одному кінці і піддану навантаженню на вільному\(P\) кінці, як показано на малюнку 2. Діаграма вільного тіла перерізу, розрізаного поперечно в положенні,\(x\) показує, що сила зсуву\(V\) та момент\(M\) повинні існувати на розрізаному перерізі для підтримки рівноваги. Ми покажемо в модулі 13, що це результанти зсувних і нормальних напружень, які встановлюються на внутрішніх площинях навантаженнями на вигин. Як завжди, ми розглянемо ділянки ділянок, нормалі яких вказують у\(x\) напрямку + як позитивні; тоді сили зсуву, що вказують у\(y\) напрямку + на\(x\) гранях +, будуть вважатися позитивними. Моменти, вектор яких напрямок, заданий правилом праворуч, знаходяться в\(z\) напрямку + (вектор поза площиною паперу або має тенденцію викликати обертання проти годинникової стрілки в площині паперу), будуть позитивними при дії на +\(x\) граней. Ще один спосіб розпізнати позитивні моменти згинання полягає в тому, що вони змушують форму вигину увігнутою вгору. Для цього прикладу пучка рівняння статики дають:
\[\sum F_y = 0 = V + P \Rightarrow V = \text{constant} = -P\]
\[\sum M_0 = 0 = -M + Px \Rightarrow M = M(x) = Px\]
Зверніть увагу, що момент збільшується з відстанню від навантаженого кінця, тому величина максимального значення в\(M\) порівнянні з\(V\) збільшується в міру того, як промінь стає довшим. Це справедливо для більшості балок, тому ефекти зсуву зазвичай важливіші в балках з невеликим співвідношенням довжини до висоти.
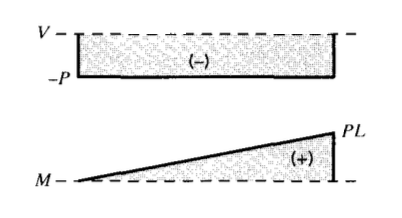
Як зазначалося раніше, напруги та відхилення будуть показані як функції\(V\) і\(M\), тому важливо мати можливість обчислити, як ці величини змінюються по довжині балки. Ділянки\(V(x)\) і\(M(x)\) відомі як діаграми зсувних і згинальних моментів, і їх необхідно отримати, перш ніж можна буде визначити напруження. Для кінцевої навантаженої консолі схеми, наведені на малюнку 3, очевидні з Eqns. 4.1.1 і 4.1.2.
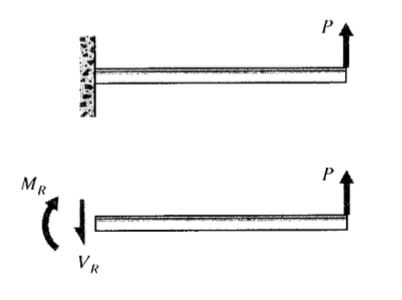
Проаналізувати консольну балку було найпростіше по початку на вільному кінці, але вибір походження довільний. Не завжди можна вгадати найпростіший спосіб вчинити, тому розглянемо, що б сталося, якби початок було розміщено біля стіни, як на малюнку 4. Тепер, коли побудована діаграма вільного тіла, сили повинні бути розміщені на початку, щоб замінити реакції, які були накладені стіною, щоб утримати промінь в рівновазі з прикладеною навантаженням. Ці реакції можуть бути визначені за діаграмами вільного тіла балки в цілому (якщо промінь статично детермінантний), і повинні бути знайдені, перш ніж проблема може продовжити. Для пучка малюнка 4:
\(\sum F_y = 0 = -V_R + P \Rightarrow V_R = P\)
Потім зсувний і згинальний момент\(x\)
\(V(x) = V_R = P = \text{constant}\)
Цей вибір походження дає деяку додаткову алгебру, але\(M(x)\) діаграми\(V(x)\) і, наведені на малюнку 5, такі ж, як і раніше (за винятком зміни знака):\(V\) постійна і дорівнює\(P\), і\(M\) змінюється лінійно від нуля на вільному\(PL\) кінці до біля стіни.
Розподілені навантаження
Поперечні навантаження можуть застосовуватися до балок розподіленим, а не точковим способом, як показано на малюнку 6, який може бути візуалізований у вигляді піску, нагромадженого на балці. Зручно описувати ці розподілені навантаження з точки зору сили на одиницю довжини, так що\(q(x)\) б навантаження, прикладена до невеликої ділянки довжини\(dx\) розподіленим навантаженням\(q(x)\). Зсувна сила,\(V(x)\) встановлена в реакції на таке навантаження, становить
\[V(x) = - \int_{x_0}^{x} q(\xi) d \xi\]
Малюнок 5: Альтернативні діаграми зсуву та згинального моменту для консольної балки.
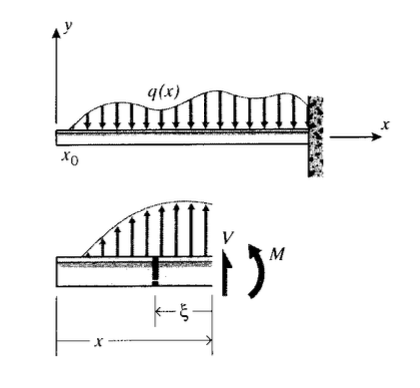
де\(x_0\) - значення, з якого\(x\) починається\ q (x)\), і\(\xi\) є фіктивною змінною довжини, яка дивиться назад\(x\). \(V(x)\)Звідси і площа під\(q(x)\) діаграмою до положення\(x\). Моментний баланс отримують з урахуванням приросту навантаження,\(q(\xi) d \xi\) прикладеного до\(d \xi\) невеликої ширини балки, відстані\(\xi\) від точки\(x\). Інкрементний момент цього навантаження навколо точки\(x\) є\(q(\xi) \xi d \xi\),\(M(x)\) тому момент
\[M = \int_{x_0}^{x} q(\xi) \xi d \xi\]
Це може бути пов'язано з центроїдом області під\(q(x)\) кривою аж до\(x\), відстань від якої\(x\) дорівнює
\(\bar{\xi} = \dfrac{\int q(\xi) \xi d \xi}{\int q (\xi) d\xi}\)
Звідси можна записати рівняння 4.1.4
\[M = Q \bar{\xi}\]
де\(Q = \int q (\xi) d\xi\) знаходиться площа. Тому розподілене навантаження\(q(x)\) статично еквівалентна зосередженому навантаженню величини,\(Q\) розміщеної в центрі площі під\(q(x)\) діаграмою.
Приклад\(\PageIndex{1}\)
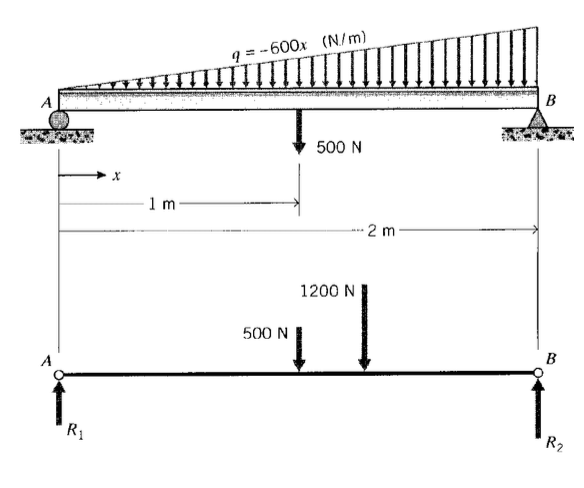
Розглянемо просту опорну балку, що несе трикутну і зосереджене навантаження, як показано на малюнку 7. З метою визначення опорних реакційних сил\(R_1\) і\(R_2\), розподілене трикутне навантаження може бути замінена її статичним еквівалентом. Величина цієї еквівалентної сили дорівнює
Еквівалентна сила діє через центроїд трикутної області, що становить 2/3 відстані від її вузького кінця (див. Ексерсис\(\PageIndex{1}\)). Реакцію тепер\(R_2\) можна знайти, взявши моменти навколо лівого кінця:
Іншу реакцію можна знайти з вертикальної рівноваги:
Послідовний метод інтеграції
Малюнок 8: Відносини між розподіленими навантаженнями та внутрішніми силами зсуву та згинальними моментами.
Ми вже відзначали в Рівнянні 4.1.3, що крива зсуву є негативним інтегралом кривої навантаження. Інший спосіб розвитку цього полягає в розгляді вільного балансу тіла на невеликому збільшенні довжини,\(dx\) протягом якого зсув і момент змінюються від\(V\) і\(M\) до\(V + dV\) і\(M + dM\) (див. Рис. Розподілене навантаження\(q(x)\) можна приймати як постійну протягом невеликого інтервалу, тому баланс сил становить:
\[\dfrac{dV}{dx} = -q\]
або
\[V(x) = - \int q(x) \ dx\]
що еквівалентно рівнянню 4.1.3. Моментний баланс навколо центру приросту дає
Коли приріст\(dx\) зменшується до межі, термін, що містить диференціал вищого порядку,\(dV\ dx\) зникає в порівнянні з іншими, залишаючи
\[\dfrac{dM}{dx} = -V\]
або
\[M(x) = -\int V(x)\ dx\]
Отже, значення кривої зсуву в будь-якому осьовому розташуванні вздовж балки дорівнює негативному нахилу кривої моменту в цій точці, а значення кривої моменту в будь-якій точці дорівнює негативній площі під кривою зсуву до цієї точки.
Криві зсуву та моменту можна отримати шляхом послідовного інтегрування\(q(x)\) розподілу, як показано на наступному прикладі.
Приклад\(\PageIndex{2}\)
Розглянемо консольну балку, що піддається негативному розподіленому навантаженню\(q(x) = -q_0\) = постійною, як показано на малюнку 9; тоді
\(V(x) = -\int q(x)\ dx = q_0 x + c_1\)
де\(c_1\) константа інтеграції. Вільна діаграма тіла невеликої тріски довжини поблизу\(x = 0\) показує\(V(0) = 0\), що, таким чином,\(c_1\) повинен бути нулем, а також. Функція моменту отримується шляхом інтеграції знову:
\(M(x) = -\int V(x) \ dx = -\dfrac{1}{2} q_0 x^2 + c_2\)
де ще\(c_2\) одна константа інтеграції, яка також дорівнює нулю, оскільки\(M(0) = 0\).
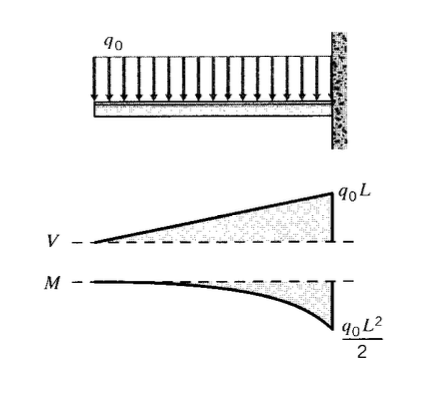
Справді, ця проблема була простою, тому що ми вибрали один з нульовими граничними умовами, і тільки з одним сегментом завантаження. Коли зосереджені або розподілені навантаження виявляються при різних
положення уздовж балки, необхідно інтегрувати над кожною секцією між навантаженнями окремо. Кожна інтеграція буде виробляти невідому константу, і вони повинні бути визначені шляхом виклику безперервності нахилів і відхилень від розділу до розділу. Це трудомісткий процес, але такий, який можна зробити набагато простіше, використовуючи функції сингулярності, які будуть введені незабаром.
Часто можна робити ескізи\(V\) та\(M\) діаграми, фактично не малюючи діаграми вільного тіла або не пишучи рівняння рівнянь рівноваги. Це полегшується, оскільки криві є інтегралами або похідними один від одного, тому графічні ескізи можуть скористатися перевагами відносин між схилами та ділянками.
Ці правила можуть бути використані для поступової роботи від\(q(x)\) кривої до\(V(x)\) і потім до\(M(x)\). Скрізь, де на промені з'являється зосереджене навантаження,\(V(x)\) крива повинна стрибати на цю величину, але у зворотному напрямку; аналогічно\(M(x)\) крива повинна стрибати безперервно скрізь, де пара прикладена до променя.
Приклад\(\PageIndex{3}\)
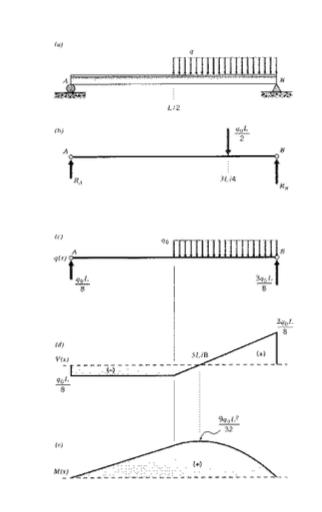
Щоб проілюструвати цей процес, розглянемо просту опорну балку довжини,\(L\) як показано на малюнку 10, навантажену на половину її довжини від'ємним розподіленим навантаженням\(q = -q_0\). Рішення для\(V(x)\) і\(M(x)\) приймає наступні кроки:
1. Реакції на опорах знаходять від статичної рівноваги. Заміна розподіленого навантаження зосередженим навантаженням\(Q = -q_0 (L/2)\) в середній точці\(q\) розподілу (рис. 10 (б)) і прийняття моментів навколо\(A\):
\(R_B L = (\dfrac{q_0L}{2}) (\dfrac{3L}{4}) \Rightarrow R_B = \dfrac{3q_0L}{8}\)
Реакція на правому кінці потім виявляється з вертикального балансу сили:
Зауважте, що було доступно лише два рівняння рівноваги, оскільки горизонтальний баланс сил не надасть відповідної інформації. Значить, балка буде статично невизначеною, якщо присутні більше двох опор.
\(q(x)\)Діаграма - це просто промінь з кінцевими реакціями, показаними на малюнку 10 (с).
2. Починаючи діаграму зсуву зліва,\(V\) відразу ж скаче вниз до значення\(-q_0 L/8\) в опозиції до розривно прикладеної сили реакції при\(A\); вона залишається на цьому значенні до тих пір,\(x = L/2\) як показано на малюнку 10 (г).
3. При\(x = L/2\),\(V(x)\) крива починає підніматися з постійним ухилом в\(+ q_0\) міру того, як площа під\(q(x)\) розподілом починає накопичуватися. Коли\(x = L\) крива зсуву підніметься на величину\(q_0 L/2\), загальна площа під\(q(x)\) кривою; її значення тоді\((-q_0 l/8) + (q_0 L/2) = (3q_0 L/8)\). Потім крива зсуву падає до нуля на противагу силі реакції\(R_B = (3q_0 L/8)\). (\(M\)Схеми\(V\) і завжди повинні закриватися, і це забезпечує перевірку роботи.)
4. Діаграма моменту починається з нуля, як показано на малюнку 10 (е), так як на лівому кінці немає розривно застосованого моменту. Він рухається вгору з постійним ухилом\(+q_0L/8\), величиною діаграми зсуву в першій половині балки. Коли\(x = L/2\), вона піднялася до значення\(q_0 L^2/16\).
5. Після\(x = L/2\), нахил діаграми моменту починає падати в міру зростання значення діаграми зсуву. Діаграма моменту тепер параболічна, завжди на порядок вище діаграми зсуву. Діаграма зсуву перетинає\(V = 0\) вісь в\(x = 5L/8\), і в цей момент нахил діаграми моменту впаде до нуля. Максимальне значення\(M\) дорівнює\(9q_0 L^2/32\), загальна площа під\(V\) кривою до цієї точки.
6. Після\(x = 5L/8\), діаграма моменту падає параболічно, досягаючи нуля при\(x = L\).
Функції сингулярності
Це спеціальне сімейство функцій забезпечує автоматичний спосіб обробки нерівностей навантаження, які зазвичай виникають при проблемах з променями. Вони багато в чому схожі на звичайні поліноміальні фактори, але з властивістю бути нулем, поки «не активуються» в потрібних точках вздовж променя. Формальним визначенням є
\[f_n (x) = \langle x - a \rangle^n = \begin{cases} 0, & x < a \\ (x - a)^n, & x > a \end{cases}\]
де\(n = -2, -1, 0, 1, 2, \cdots\). Функція\(\langle x - a \rangle^0\) є одиничною функцією кроку,\(\langle x - a \rangle_{-1}\) є зосередженим навантаженням і\(\langle x - a \rangle_{-2}\) є концентрованою парою. Перші п'ять з цих функцій намальовані на малюнку 11.
Малюнок 11: Функції сингулярності.
Функції сингулярності інтегровані так само, як звичайні поліноми:
\[\int_{-\infty}^{x} \langle x - a \rangle^n \ dx = \dfrac{\langle x - a \rangle^{n+1}}{n + 1} \ n \ge 0\]
Однак існують спеціальні правила інтеграції для\(n = -2\) членів and,\(n = -1\) і ця особлива обробка підкреслюється використанням індексів для\(n\) індексу:
\[\int_{\infty}^{x} \langle x - a \rangle_{-2}\ dx = \langle x - a \rangle_{-1}\]
\[\int_{\infty}^{x} \langle x - a \rangle_{-1}\ dx = \langle x - a \rangle^0\]
Приклад\(\PageIndex{4}\)
Застосовуючи функції сингулярності до променя Прикладу 4.3, функція завантаження буде записана
Сила реакції на правому кінці також може бути включена, але вона активізується тільки в міру того, як проблема закінчена. Інтеграція один раз:
Константа інтеграції включається автоматично сюди, оскільки вплив реакції на\(A\) був включений явно. Інтеграція знову:
Експертиза цього результату покаже, що він такий же, як і розроблений раніше.
Maple\(^{\text{TM}}\) символічні маніпуляції програмного забезпечення забезпечує ефективний засіб побудови цих функцій. Нижче показано, як може бути побудовано рівняння моменту у цьому прикладі, використовуючи функцію Хевісайда для забезпечення сингулярності.
# Define function sfn in terms of a and n
>sfn:=proc(a,n) (x-a)^n*Heaviside(x-a) end;
sfn := proc(a, n) (x - a)^n*Heaviside(x - a) end proc
# Input moment equation using singularity functions
>M(x):=(q*L/8)*sfn(0,1)-(q/2)*sfn(L/2,2);
M(x) := 1/8 q L x Heaviside(x) 2
-1/2q(x-1/2L) Heaviside(x-1/2L)
# Provide numerical values for q and L: >q:=1: L:=10:
# Plot function >plot(M(x),x=0..10);
Малюнок 12: Сюжет сингулярності клена
Вправа\(\PageIndex{1}\)
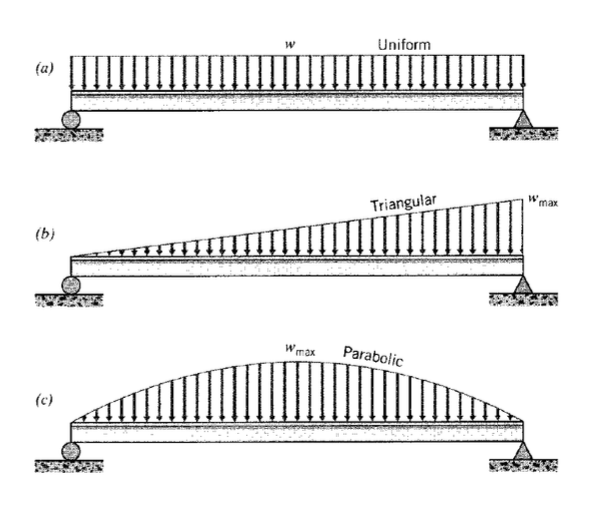
(a) - (c) Знайдіть величину та положення сили, еквівалентні розподілам навантаження, показаним тут.
Вправа\(\PageIndex{2}\)
(a) - (c) Визначити сили реакції на опорах корпусів у навчанні\(\PageIndex{1}\).
Вправа\(\PageIndex{3}\)
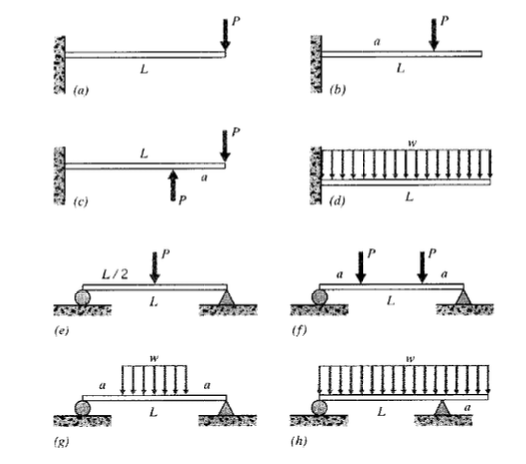
(a) - (h) Намалюйте діаграми зсувного та згинального моменту для випадків навантаження, показаних тут.
Вправа\(\PageIndex{4}\)
(a) - (h) Напишіть вирази особливої-функції для розподілів зсувних та згинальних моментів для випадків у вправі\(\PageIndex{3}\).
Вправа\(\PageIndex{5}\)
(a) - (h) Використовуйте Maple (або інше) програмне забезпечення для побудови розподілу зсувних та згинальних моментів для випадків у Вправі\(\PageIndex{3}\), використовуючи значення (за потребою)\(L = 25 \ in, a = 5\ in, w = 10\ lb/in, P = 150 \ lb\).
Вправа\(\PageIndex{6}\)
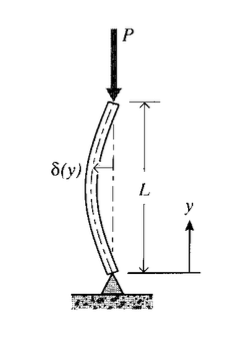
Поперечний прогин\(n\) балки під осьовим навантаженням\(P\) приймається рівним\(\delta (y) = \delta_0 \sin (y \pi /L)\), як показано тут. Визначте згинальний момент\(M(y)\) уздовж балки.
Вправа\(\PageIndex{7}\)
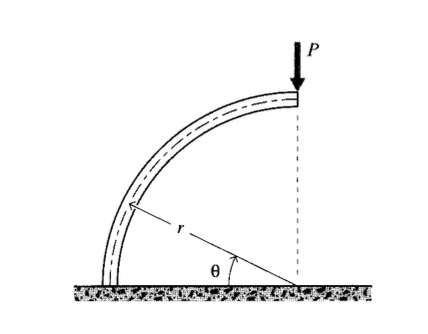
Визначте згинальний момент\(M(\theta)\) по зображеному круговому вигнутому балці.