11.3: нестисливість

Численні експерименти, проведені за минулі 100%, показали, що метали практично нестисливі в пластичному діапазоні. Давайте розберемо наслідки цього фізичного факту в разі одновимірного випадку. Позначимо величину довжини призматичного бруса по\(l\) і площа його поперечного перерізу по\(A\). Поточний обсяг секції калібру дорівнює\(V = Al\). Нестисливість означає, що обсяг повинен бути незмінним або\(dV = 0\).

\[dV = d(Al) = dAl + Adl = 0 \label{11.3.1}\]

З Equation\ ref {11.3.1} робимо висновок, що приріст деформації\(d\epsilon\) можна обчислити або шляхом відстеження довжини датчика або площі поперечного перерізу

\[d\epsilon = \frac{dl}{l} = − \frac{dA}{A} \label{eq0}\]

Інтеграція першої частини рівняння\ ref {eq0}

\[\epsilon = \ln l + C_1 \]

Константа інтеграції отримується, вимагаючи, щоб деформація зникла, коли довжина\(l\) дорівнює початковій, еталонній довжині\(l_o\), яка дає\(C = − \ln l_o\). Таким чином

\[\epsilon = \ln \frac{l}{l_o} \label{eq1}\]

що є логарифмічним визначенням деформації, введене в главі 1. Аналогічно, інтегруючи другу частину Equation\ ref {eq0} з початковою умовою at\(A = A_o\)\(\epsilon = 0\), один отримує

\[\epsilon = \ln \frac{A_o}{A} \label{eq2}\]

У напрузі\(l > l_o\) або\(A < A_o\), отже, обидва рівняння\ ref {eq1} і\ ref {eq2} дають позитивну деформацію. При стисненні деформація негативна. Те ж саме стосується приросту деформації\(d\epsilon\) або швидкості деформації

\[\dot{\epsilon} = \frac{\dot{l}}{l} \quad \text{ or } \quad \dot{\epsilon} = − \frac{\dot{A}}{A} \]

З наведеного вище аналізу випливає просте розширення умови пластичної нестисливості в 3-D корпус. Розглянемо нескінченно малий об'ємний елемент\(V = x_1x_2x_3\), Рисунок (\(\PageIndex{1}\))

Малюнок\(\PageIndex{1}\): Неформовані та деформовані 1-D та 3-D об'ємні елементи.

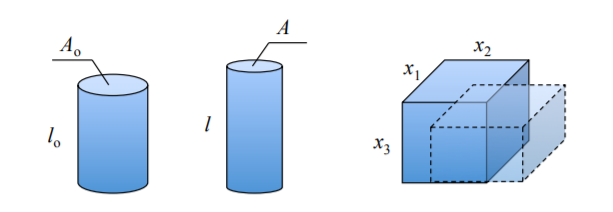
Пластична нестисливість вимагає, щоб

\[dV = d(x_1x_2x_3) = dx_1(x_2x_3) + x_1d(x_2x_3) \\ = dx_1x_2x_3 + x_1dx_2x_3 + x_1x_2dx_3 \]

Розділивши обидві сторони вищевказаного рівняння на об'єм, отримують

\[\frac{dx_1}{x_1} + \frac{dx_2}{x_2} + \frac{dx_3}{x_3} = 0 \]

або

\[d\epsilon_{11} + d\epsilon_{22} + d\epsilon_{33} = 0, \quad d\epsilon_{kk} = 0 \nonumber \]

Відзначаючи\(d\epsilon_{11} = \frac{\partial \epsilon_{11}}{\partial t} dt = \dot{\epsilon}_{11}dt\), що альтернативною формою стану нестисливості є

\[\dot{\epsilon}_{11} + \dot{\epsilon}_{22} + \dot{\epsilon}_{33} = 0, \quad \dot{\epsilon}_{kk} = 0 \]

Сума діагональних складових тензора швидкості деформації повинна зникнути, щоб забезпечити нестисливість. З правила потоку (буде сформульовано пізніше) випливає, що при одновісному натягу в\(x_1\) напрямку компоненти\(\dot{\epsilon}_{22} = \dot{\epsilon}_{33}\). Тому\(\dot{\epsilon}_{11} + 2\dot{\epsilon}_{22} = 0\) або\(\dot{\epsilon}_{11} + 2\dot{\epsilon}_{33} = 0\). Нарешті отримуємо

\[\dot{\epsilon}_{22} = −0.5\dot{\epsilon}_{11}, \quad \dot{\epsilon}_{33} = −0.5\dot{\epsilon}_{11} \]

Коефіцієнт 0,5 можна інтерпретувати як коефіцієнт Пуассона

\[\nu = − \frac{\dot{\epsilon}_{22}}{\dot{\epsilon}_{11}} = − \frac{\dot{\epsilon}_{33}}{\dot{\epsilon}_{11}} = 0.5 \]

Можна зробити висновок, що пластична нестисливість вимагає, щоб відношення Пуассона було рівним\(1/2\), яке відрізняється від пружного відношення Пуассона, рівного\(\tilde 0.3\) для металів. Багато інших матеріалів, таких як гума, полімери та вода, є нестисливими.